Analisi modale con spettro di risposta: tutti i dettagli del calcolo

L’analisi di una costruzione in zona sismica richiede l’esecuzione dell’analisi modale con spettro di risposta, un tipo di analisi che rientra fra i metodi proposti dalla Normativa Tecnica, nella categoria dell’analisi dinamica lineare.

In quest’articolo ti mostro come si determina l’azione sismica agente su una costruzione utilizzando i modi di vibrare ottenuti dall’analisi modale e gli spettri di risposta forniti dalle NTC2018. Vedremo come influisce sul risultato finale la massa partecipante e i fattori di partecipazione modale e come si combinano fra loro i contributi di ciascun modo per ottenere la risposta massima del sistema in termini di sollecitazioni e spostamenti.

Alla fine dell’articolo potrai scaricare una risorsa utility interattiva che riproduce i modi di vibrare di un telaio piano a due livelli e potrai vedere un video esplicativo che riassume, mediante animazioni, il procedimento di calcolo dell’analisi modale con spettro di risposta. Continua a leggere, scoprirai qual è il collegamento fra analisi modale e spettri di risposta per il calcolo delle costruzioni in zona sismica.

---

Scarica EarthQuake: la guida pratica per l’analisi sismica delle strutture

---

Analisi modale e spettri di risposta: un breve riepilogo

Ti ho già parlato in altri articoli del blog dell’analisi modale (come capirla in 6 minuti e come capirla grazie a delle palle da baseball) e degli spettri di risposta (sai che sono stati ottenuti grazie ad un lollipop?). Ti riporto qui di seguito un breve riepilogo.

Cosa fa l’analisi modale

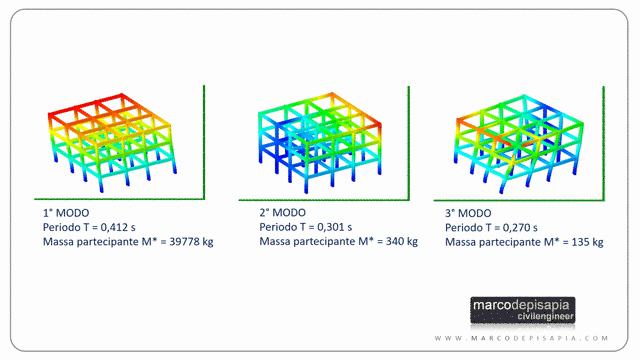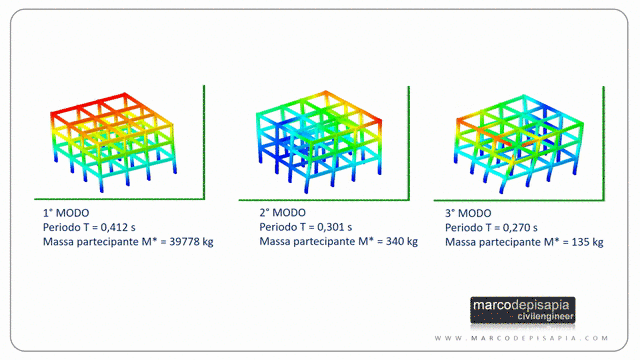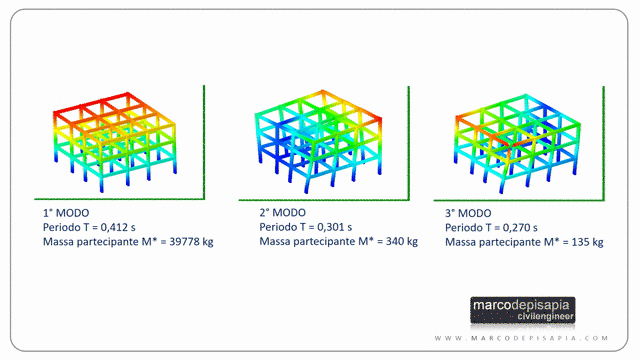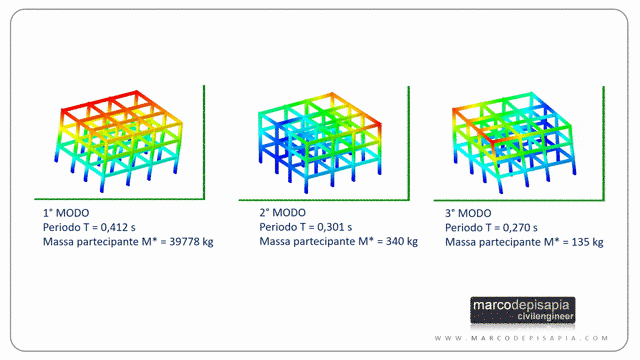
L’analisi modale calcola i modi di vibrare di una struttura, il periodo proprio di vibrazione associato ad ogni modo di vibrare e la massa partecipante eccitata in ciascun modo di vibrare. I modi di vibrare sono quelle configurazioni deformate per le quali lo spostamento di ciascun punto della struttura, lasciata libera di oscillare in assenza di smorzamento, è proporzionale in ogni istante allo spostamento di qualsiasi altro punto.

Un modo di vibrare si può anche definire come quella particolare configurazione deformata per la quale lo spostamento di ogni nodo della struttura, lasciata libera di oscillare, avrà un andamento sinusoidale in funzione del tempo.

Cosa sono gli spettri di risposta

Gli spettri di risposta rappresentano, in funzione del periodo di vibrazione (in genere il range di variazione va da 0 a 4 secondi circa), quale accelerazione massima subirebbe un sistema vibrante ad un solo grado di libertà (un oscillatore semplice per la precisione) sottoposto ad una serie di accelerogrammi rappresentativi di eventi sismici con periodo di ritorno dato dallo Stato Limite considerato (475 anni per Stato Limite di Salvaguardia della vita, SLV).

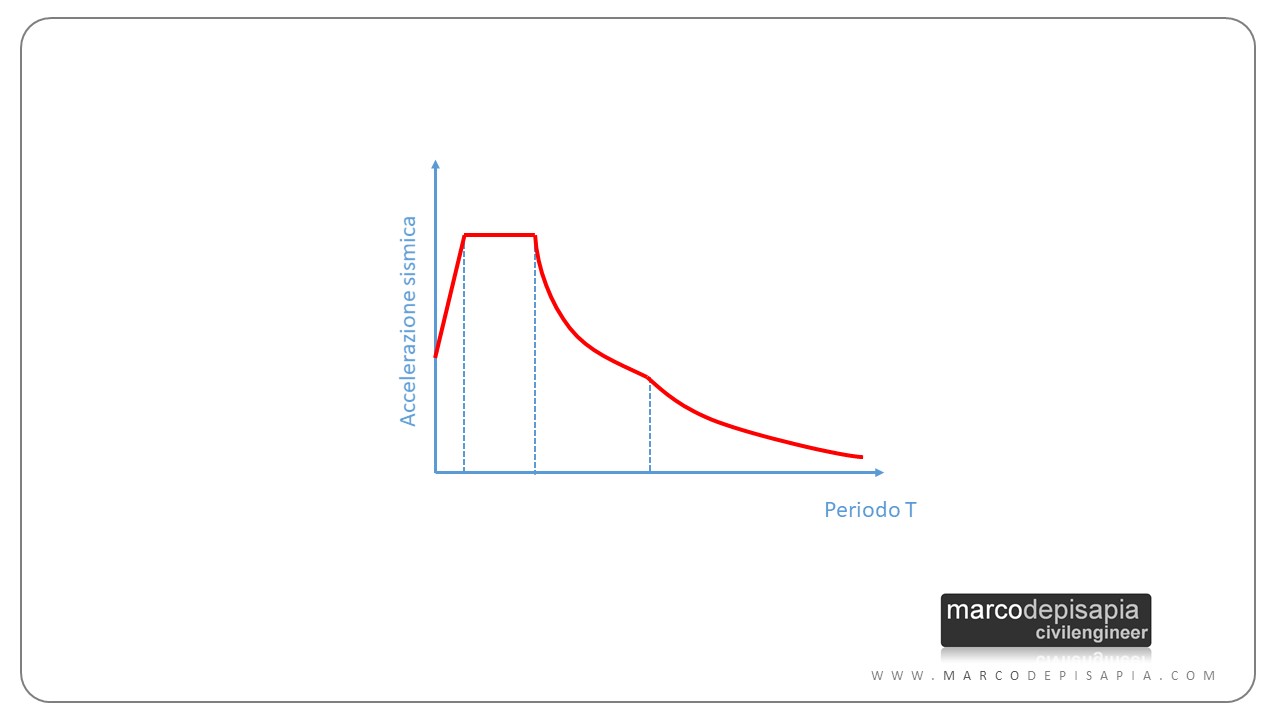
Analisi modale con spettro di risposta: oscillatore semplice (SDOF) e struttura completa (MDOF)

Come appena visto, l’analisi modale calcola i modi di vibrare di una struttura, i periodi di vibrazione e la massa partecipante associati a ciascun modo di vibrare. Gli spettri di risposta mettono in relazione in un grafico il periodo proprio di vibrazione di un oscillatore semplice con l’accelerazione massima che il sistema subirebbe se sottoposto ad una serie di accelerogrammi con un definito periodo di ritorno.

Quello che succede dopo potrebbe essere un po’ meno chiaro: come si combinano questi due elementi (modi di vibrare e spettro di risposta) per ottenere l’azione sismica agente sulla struttura? Continua a leggere per scoprirlo.

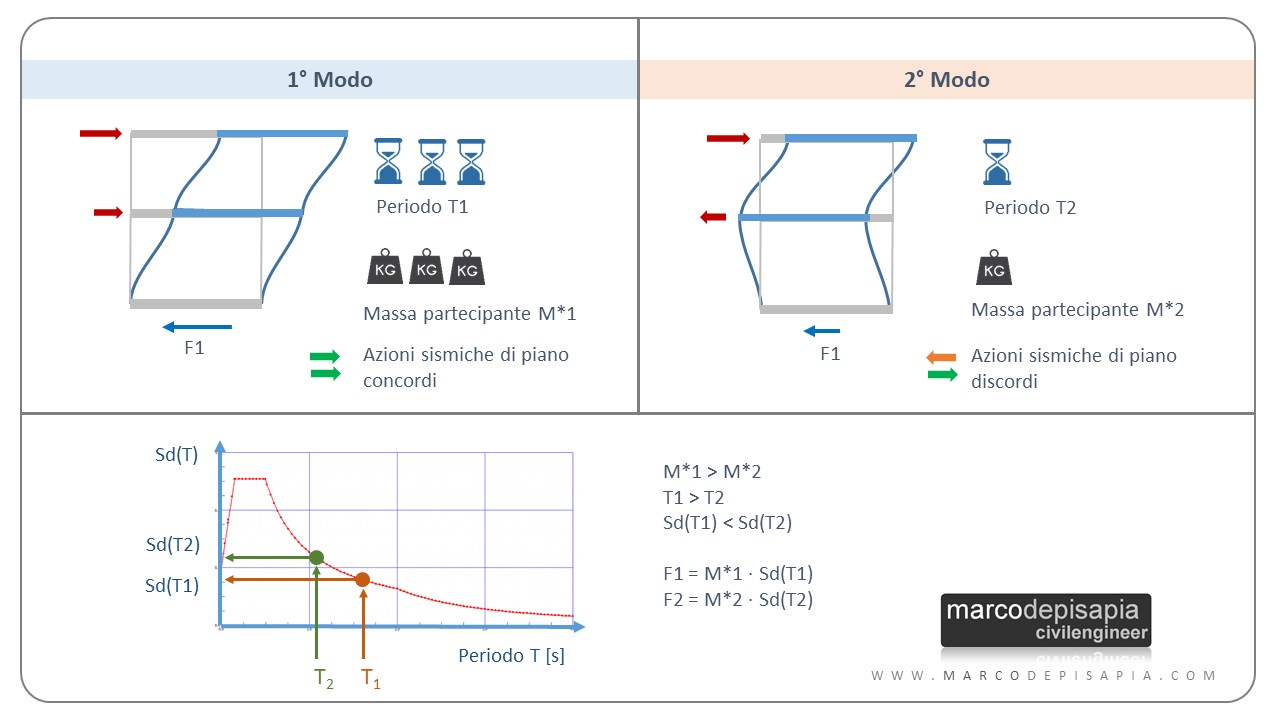
Come detto sopra, ciascun modo di vibrare avrà un suo periodo di vibrazione e una massa partecipante. I modi di vibrare sono ordinati per periodi di vibrazione decrescenti. Il primo modo di vibrare avrà il periodo maggiore, il secondo modo avrà un periodo minore del primo e maggiore del terzo e così via.

Per ciascun modo di vibrare, la struttura a più gradi di libertà (anche definita come MDOF = multi-degree of freedom) può essere schematizzata come un oscillatore semplice (SDOF = single degree of freedom) dotato del periodo di vibrazione del singolo modo e della massa partecipante del modo.

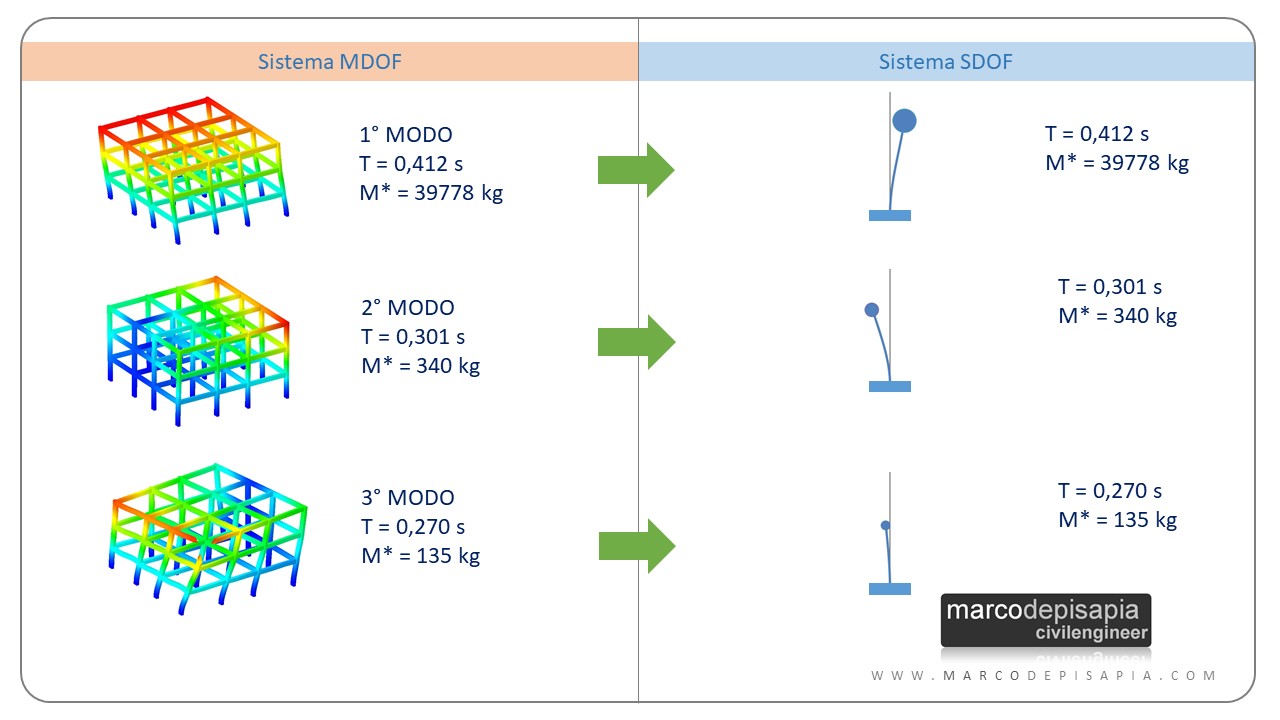
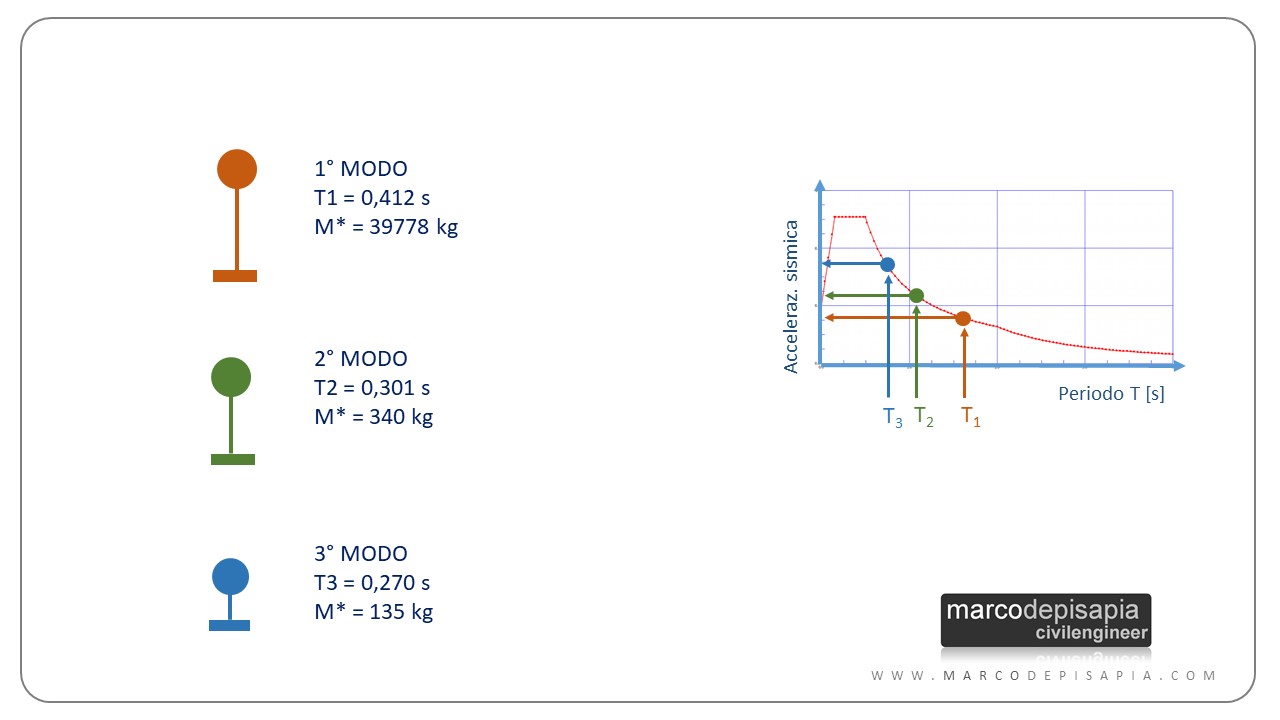
Pertanto si può estrapolare dallo spettro di risposta l’accelerazione sismica corrispondente al periodo proprio di vibrazione. Moltiplicando la massa partecipante del modo di vibrare per l’accelerazione sismica ottenuta dallo spettro di risposta, otterremo il tagliante sismico alla base che caratterizza quel modo di vibrare.

F_h,i = M_i* ⋅ S_d(T_i)

• F_h,i = tagliante sismico del modo di vibrare i-esimo;
• M_i* = massa partecipante del modo di vibrare i-esimo;
• S_d(T_i) = accelerazione spettrale corrispondente al periodo proprio di vibrazione T_i del modo di vibrare i-esimo.

Nei tabulati generati da un software di calcolo strutturale generalmente per ogni modo di vibrare potrai leggere il periodo di vibrazione e la massa partecipante espressa come percentuale della massa sismica totale.

Dal sistema SDOF al sistema MDOF: distribuzione del tagliante sismico in altezza

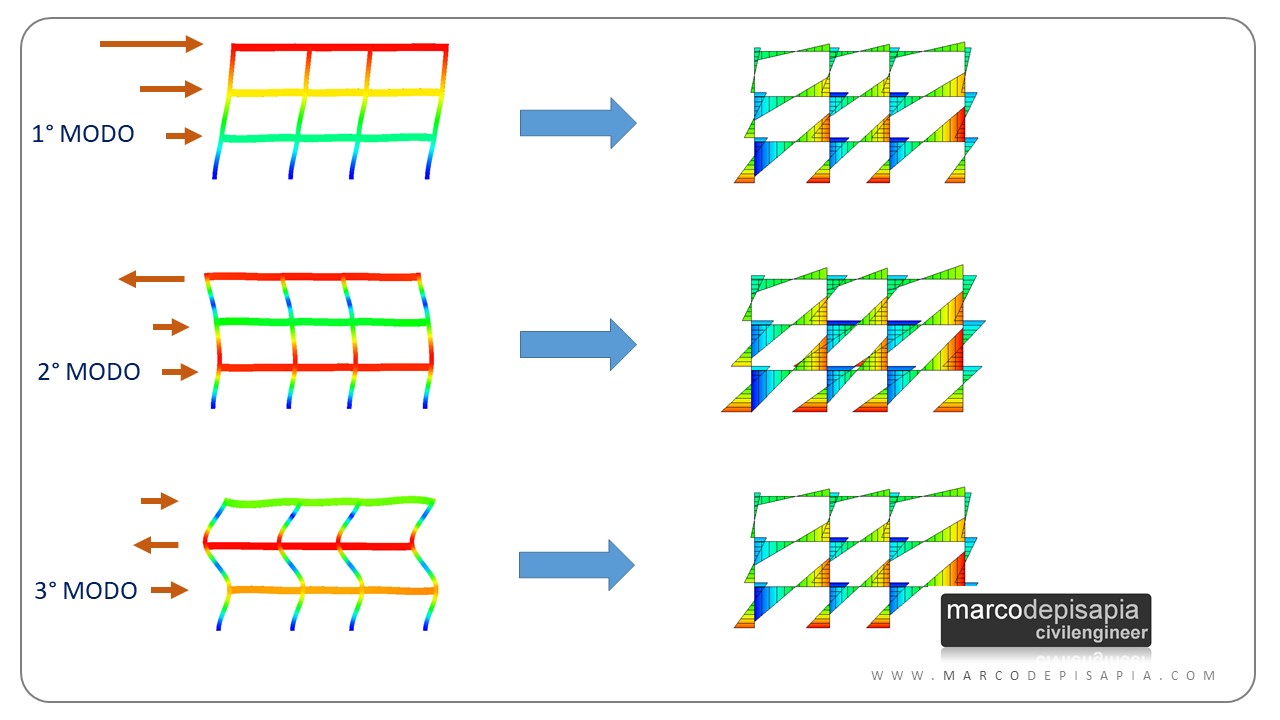
Il tagliante sismico alla base viene distribuito in altezza, alla quota delle masse di impalcato, in funzione del coefficiente di partecipazione modale, della massa di ciascun impalcato e dello spostamento di piano del modo di vibrare. Ti riporto di seguito un’immagine esplicativa relativa ad un telaio piano.

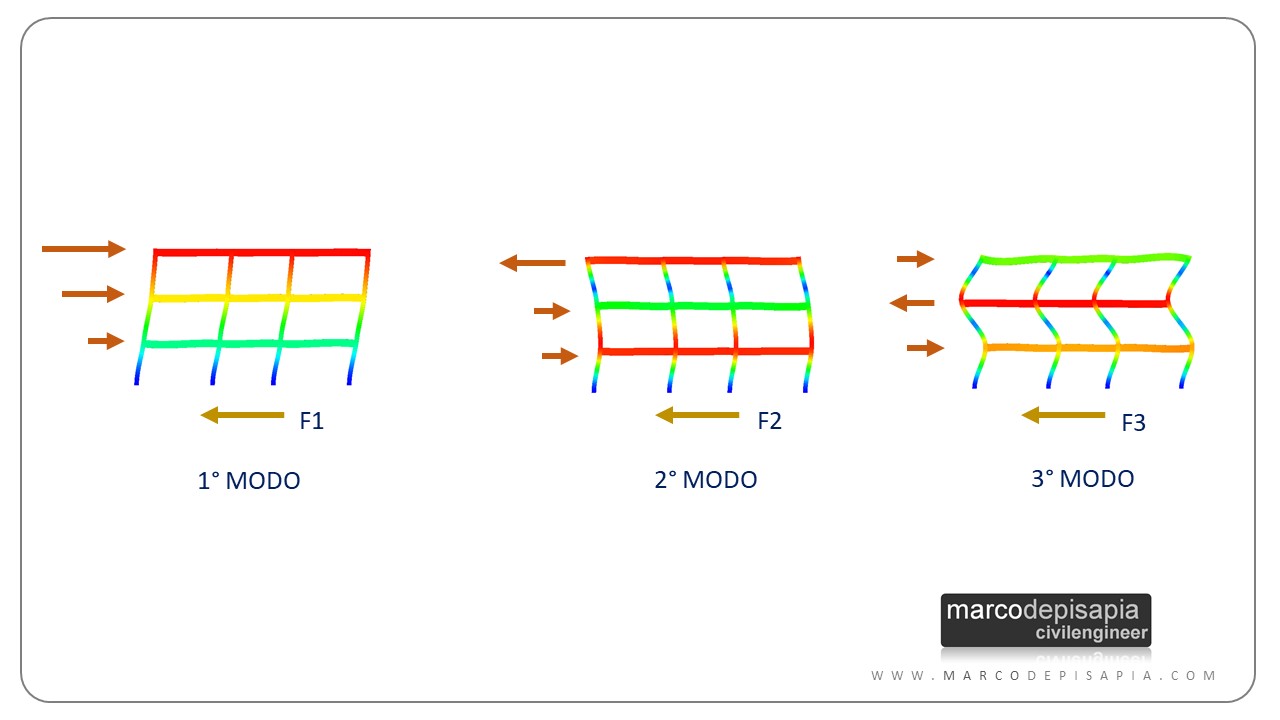
Per una struttura spaziale la distribuzione delle forze di piano è meno intuitiva, poiché entrano in gioco gli effetti di rotazione torsionale dell’impalcato e l’accoppiamento fra traslazione e rotazione dei modi di vibrare, ma comunque il concetto di base resta lo stesso.

SRSS o CQC: come combinare le sollecitazioni dei singoli modi di vibrare

Una volta noto, per ogni modo di vibrare, l’effetto massimo in termini di sollecitazioni e spostamenti in ogni punto della struttura oggetto di analisi, bisognerà valutare l‘effetto globale, considerando il contributo di ciascun modo di vibrare alla risposta massima.

Intuitivamente si potrebbe pensare di sommare le sollecitazioni ottenute per ciascun modo di vibrare. In realtà questa non è il metodo corretto per sovrapporre gli effetti dei singoli modi di vibrare.

I valori massimi in termini di spostamento e sollecitazioni, associati ai diversi modi di vibrare, non si verificano nello stesso istante, ma in istanti diversi della storia temporale della risposta della struttura. Pertanto non è corretto sommare effetti che non sono contemporanei.

Per combinare gli effetti dell’azione sismica considerandone la non-contemporaneità, esistono due metodi alternativi:

• Metodo SRSS: radice quadrata della somma dei quadrati delle sollecitazioni o degli spostamenti di tutti i modi di vibrare. Può essere utilizzato quando i modi di vibrare sono disaccoppiati fra loro;
• Metodo CQC (combinazione quadratica completa): è il metodo che le NTC2018 prescrivono di utilizzare. E’ un metodo di combinazione più accurato rispetto al metodo SRSS e tiene conto dell’accoppiamento dei modi di vibrare mediante coefficienti di correlazione e il rapporto fra i periodi dei diversi modi.

Risposta del sistema MDOF: quale modo di vibrare contribuisce di più?

Abbiamo appena visto come combinare gli effetti dei singoli modi di vibrare. E’ utile a questo punto fare delle considerazioni sull’entità del contributo di ciascun modo alla risposta massima del sistema. Quale modo contribuisce con una maggiore aliquota? I modi con periodi maggiori e massa partecipante maggiore? Quelli con periodi minori e massa partecipante minore?

Solitamente per una struttura spaziale i primi tre modi di vibrare danno il contributo maggiore alla risposta sismica globale, ma non è una regola generale e non è sempre semplice stabilirlo a priori. Vediamo perché:

• il tagliante sismico per ogni modo di vibrare è dato dal prodotto della massa partecipante del modo per l‘accelerazione spettrale corrispondente;
• per una struttura tridimensionale solitamente i primi 3 modi di vibrare hanno massa partecipante maggiore, ma accelerazioni spettrali più basse perché il periodo di vibrazione sarà maggiore;
• i  modi successivi ai primi tre invece avranno massa partecipante minore, ma accelerazioni spettrali più alte, perché il loro periodo di vibrazione sarà minore;
• la deformata dei primi 3 modi di vibrare porta a spostamenti dei nodi tutti nello stesso verso (a meno di evidenti effetti torsionali). Di conseguenza le forze sismiche corrispondenti avranno verso concorde e il tagliante sismico alla base della struttura sarà maggiore rispetto al tagliante dei modi successivi i cui le forze orizzontali hanno verso discorde fra i vari impalcati.

Ti riporto qui sotto l’immagine di un telaio piano a due livelli che sintetizza quanto appena detto.

Scarica la risorsa utility sull’analisi modale

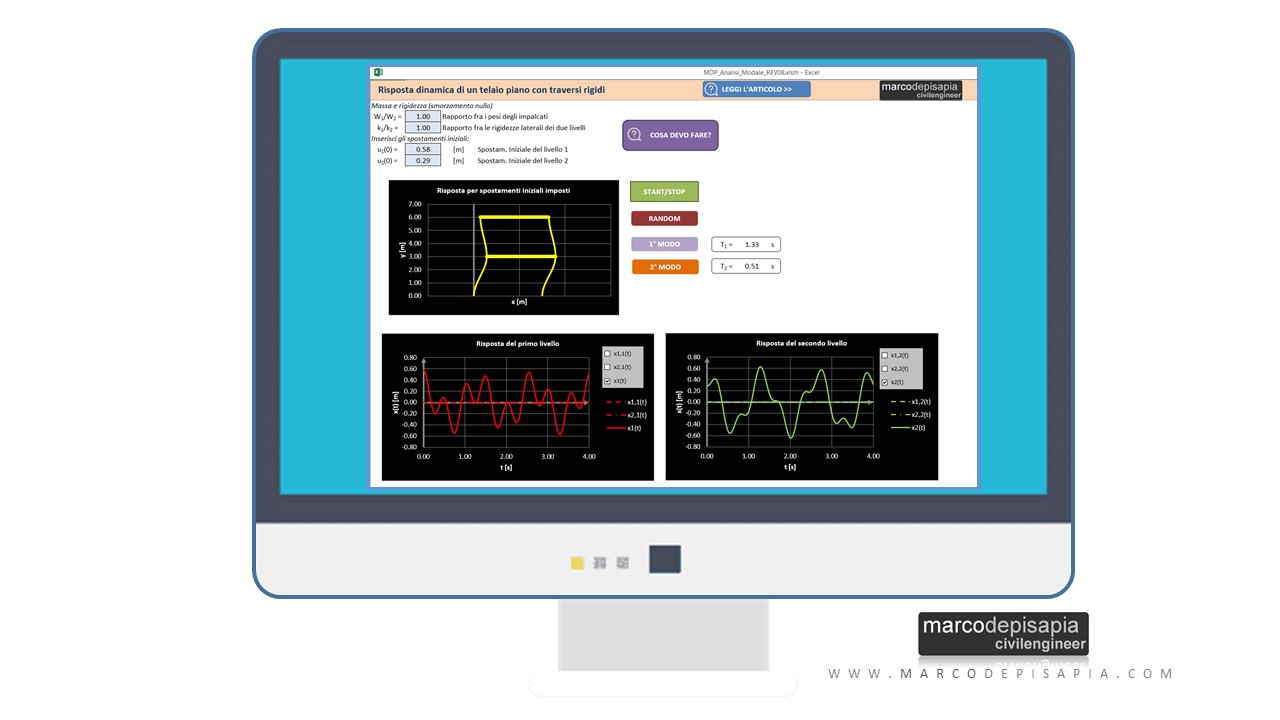
Di seguito puoi scaricare una risorsa utility che riproduce mediante animazioni interattive i modi di vibrare di un telaio piano a due livelli con traversi rigidi. Compila i campi qui sotto per scaricare la risorsa. Riceverai all’istante una e-mail contenente il link per eseguire il download.

Guarda il video sull’analisi modale con spettro di risposta

In questo video di pochi minuti ti riassumo il contenuto dell’articolo. Potrai vedere, mediante animazioni, come funziona l’analisi modale con spettro di risposta. Non perdertelo.

---

Conclusioni

L’analisi modale con spettro di risposta è un metodo di calcolo abbastanza complesso. Sarebbe impossibile eseguirla senza utilizzare un software di analisi. Ti riassumo qui di seguito i passaggi:

• determinazione dei modi di vibrare della struttura (analisi modale);
• calcolo degli effetti dell’azione sismica (sollecitazioni o spostamenti) per ciascun modo di vibrare utilizzando lo spettro di risposta;
• combinazione di questi effetti tramite un metodo di comprovata validità (CQC come prescritto dalle NTC2018).

A causa della complessità dell’analisi, risulta difficile per un progettista strutturale prevedere intuitivamente i risultati come potrebbe accadere per un telaio piano analizzato mediante analisi statica lineare.

Non è sempre semplice per i professionisti restare al passo con l’evoluzione dei metodi di calcolo e gli aggiornamenti dei software di analisi. Per questo motivo ho creato Calculation WEB, il servizio di calcolo strutturale dedicato in esclusiva ai professionisti del settore delle costruzioni. Scopri come funziona a questo link.

Siamo arrivati alla fine del post. Se hai letto fin qui allora l’analisi delle costruzioni in zona sismica fa parte del tuo settore di interesse. Spero che quest’articolo ti abbia aiutato a capire i principi fondamentali dell’analisi modale con spettro di risposta contribuendo a rendere i risultati ottenuti da un software di calcolo molto meno misteriosi.

Se l’articolo ti è piaciuto e l’hai trovato utile consiglialo ai tuoi colleghi su Linkedin o ai tuoi amici su Facebook cliccando sui tasti di condivisione social che trovi in fondo alla pagina. Se non vuoi perderti nessun nuovo articolo clicca sul tasto Mi piace della pagina Facebook del blog, visualizzerai 5 post di approfondimento a settimana nel tuo feed.

Al prossimo articolo.

Marco

---

Ultimo aggiornamento: 15/11/2020. Pubblicato il 3/4/2017.