Modi di vibrare: un esperimento illuminante (con delle palle da baseball)

La determinazione dei modi di vibrare di una struttura è necessaria quando si esegue il calcolo di una costruzione in zona sismica. Ma sai di preciso cosa sono i modi di vibrare e qual è il loro significato fisico? In quest’articolo ti mostro il video di un esperimento eseguito all’Università della Pennsylvania che ti aiuterà a capire in pochi minuti cosa sono i modi di vibrare di un sistema strutturale. L’esperimento è stato realizzato utilizzando degli oggetti di uso comune che non ti aspetteresti. Alla fine dell’articolo ti propongo un ulteriore video che riproduce il comportamento dinamico di un telaio piano a tre livelli. 

La Normativa Tecnica cita i modi di vibrare nel paragrafo del capitolo 7 dedicato all’analisi dinamica lineare, il tuo software di calcolo ha un tasto dedicato per visualizzarli, le caratteristiche dei modi di vibrare vengono sempre riportate nei fascicoli di calcolo di una struttura. Continua a leggere per capire cosa sono i modi di vibrare.

Nel corso dell’articolo potrai inoltre scaricare un estratto di EarthQuake, la guida pratica per l’analisi sismica delle strutture. Buona lettura!

---

Scarica EarthQuake: la guida pratica per l’analisi sismica delle strutture

---

I modi di vibrare riprodotti con delle palle da baseball: guarda il video

Entriamo subito nel vivo dell’articolo con il video dell’esperimento eseguito dal prof. Daniel A. Russel, professore di acustica all’Università della Pennsylvania (USA). Quali sofisticate strumentazioni avrà usato il Prof. Russel per eseguire questo test sperimentale in grado di mostrare in maniera chiarissima cosa sono i modi di vibrare? Sono bastati semplicemente degli elastici e delle palle da baseball. Ad essere precisi per l’esperimento sono state utilizzate delle wiffle balls, delle palle di plastica cave all’interno, più leggere rispetto alle classiche palle da baseball rivestite in cuoio, utilizzate negli Stati Uniti per praticare una variante del gioco del baseball.

Il sistema oscillante creato assemblando elastici e wiffle balls è un sistema dotato di  un numero di gradi di libertà di volta in volta crescente. Per ogni configurazione del sistema, l’unico grado di libertà è lo spostamento verticale di ciascuna wiffle ball. I gradi di libertà saranno pari al  numero di palle presenti in ciascuna configurazione. Aggiungendo una wiffle ball al sistema, si incrementerà di un’unità il numero di gradi di libertà. 

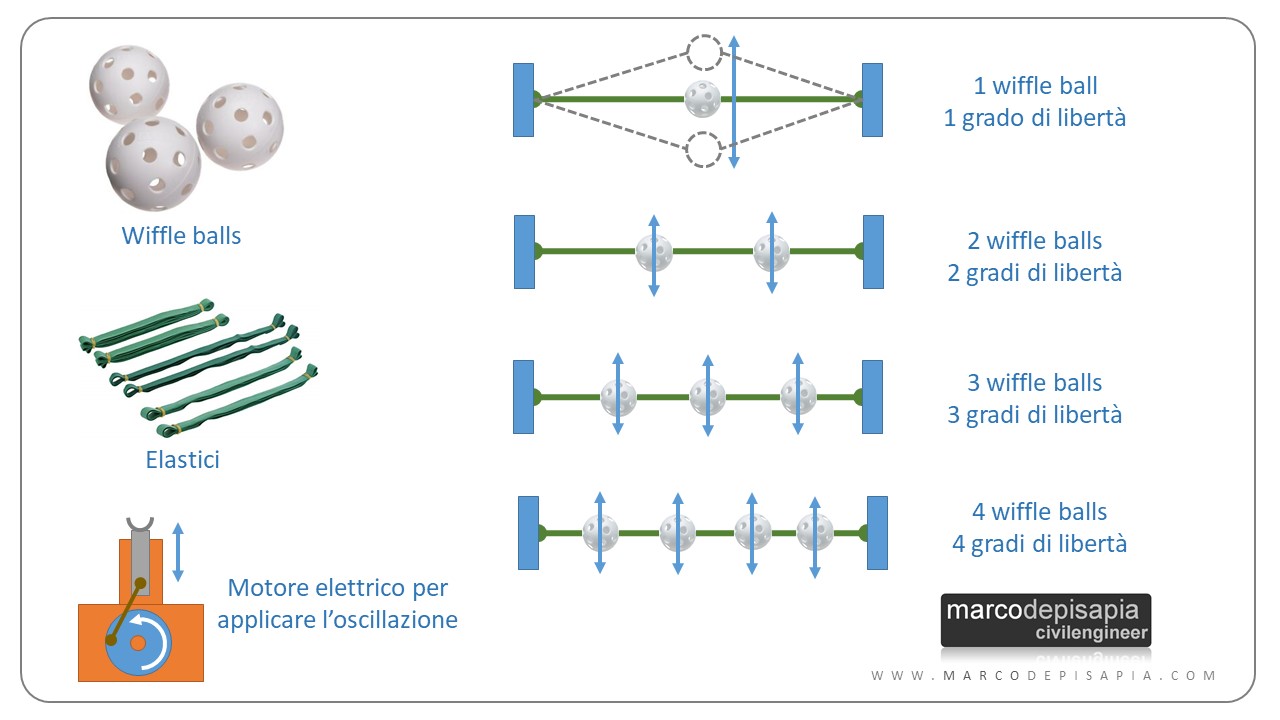
Nell’esperimento del video si parte da un solo grado di libertà (una sola wiffle ball) per arrivare fino a 4 gradi di libertà (quattro wiffle ball). Un motore elettrico applica al sistema delle vibrazioni di frequenza crescente, mandandolo in risonanza in corrispondenza delle frequenze naturali di vibrazione per ciascun modo di vibrare. Il video dura poco più di 3 minuti. Puoi visualizzare direttamente i minuti salienti indicati qui sotto:

Sistema ad 1 grado di libertà

• minuto 0:11 → 1° modo di vibrare

Sistema a 2 gradi di libertà

• minuto 0:33 → 1° modo di vibrare
• minuto 0:52 → 2° modo di vibrare

Sistema a 3 gradi di libertà

• minuto 1:15 → 1° modo di vibrare
• minuto 1:36 → 2° modo di vibrare
• minuto 1:54 → 3° modo di vibrare

Sistema a 4 gradi di libertà

• minuto 2:18 → 1° modo di vibrare
• minuto 2:46 → 2° modo di vibrare
• minuto 3:05 → 3° modo di vibrare
• minuto 3:25 → 4° modo di vibrare

Clicca sul tasto play per guardare il video sui modi di vibrare

I modi di vibrare di un sistema vengono ordinati per periodo di vibrazione decrescente. Il primo modo di vibrare sarà il modo con il periodo di vibrazione massimo. Il secondo modo di vibrare avrà un periodo di vibrazione inferiore a quello del primo modo, ma maggiore del periodo del terzo modo. E così via.

Come determinare il numero di modi di vibrare

La regola è semplice: un qualunque sistema vibrante ha tanti modi di vibrare quanti sono i suoi gradi di libertà. I gradi di libertà sono dei parametri indipendenti di spostamento o rotazione che definiscono la configurazione deformata di un sistema. Esempio: un pendolo semplice che può oscillare nel suo piano è un sistema fisico che ha un solo grado di libertà, l’angolo che l’asta del pendolo forma con la verticale (te ne ho parlato in quest’articolo sull’analisi modale).

Modi di vibrare: i nodi della deformata modale

Nel video dell’esperimento viene messo in evidenza il concetto di nodo della deformata modale. Il nodo è il punto di nullo per cui passa la deformata modale del sistema. Se ci fai caso riguardando il video, per alcuni modi di vibrare ci sono dei punti della deformata che non si spostano, restano nella loro posizione di nullo mentre il resto del sistema continua ad oscillare. Tali punti di nullo della deformata vengono chiamati nodi. 

I punti di nullo della deformata di un modo di vibrare sono pari al numero ordinale del modo di vibrare (primo modo, secondo modo, terzo modo…)  meno 1. Il primo modo avrà zero nodi (1 – 1 = 0), il secondo modo avrà un solo nodo (2 – 1 = 1), il terzo modo avrà due nodi (3 – 1 = 2), il quarto modo ne avrà tre (4 – 1 = 3) e così via.

Per ogni modo di vibrare del sistema dell’esperimento ti riporto i nodi della deformata modale evidenziati nelle immagini qui sotto.

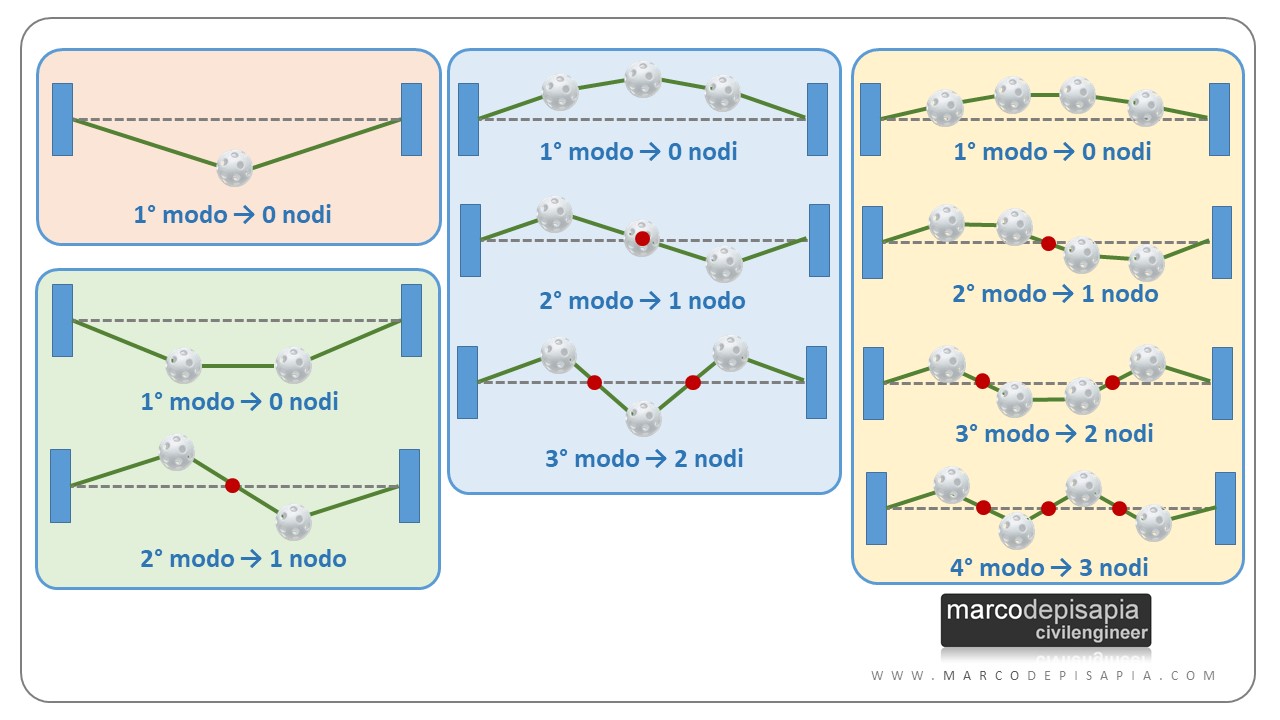
Dalle palle da baseball alle strutture reali

Sono sicuro che avrai trovato l’esperimento del prof. Russel molto interessante, ma scommetto che ti starai chiedendo: “A cosa mi serve sapere come oscillano delle palle da baseball?“

L’esperimento del video mostra molto bene cosa sono i modi di vibrare, ma in sostanza ad un progettista strutturale, ai fini della progettazione e calcolo di un edificio, interessa sapere cosa succede quando il sistema vibrante non è fatto di palle da baseball ed elastici, ma è una struttura reale. In questo caso valgono gli stessi concetti visti sopra. Una struttura è un sistema vibrante che ha un certo numero di gradi di libertà. Pertanto, come hai potuto vedere dal video dell’esperimento, avrà un numero di modi di vibrare pari al numero dei suoi gradi di libertà.

Telaio piano a tre livelli: i modi di vibrare mostrati in un esperimento

Voglio mostrarti il video di un altro esperimento. E’ simile a quello visto sopra, ma questa volta il modellino è più attinente al nostro scopo. Si tratta di un telaio piano a tre livelli con traversi rigidi. Il modellino ha tre gradi di libertà: lo spostamento orizzontale di ciascun livello. Su ogni livello è stata collocata una massa concentrata. Alla base del modellino una macchina applica un’oscillazione di frequenza man mano crescente. Puoi selezionare direttamente i minuti seguenti nel video:

• minuto 0:20 si attiva il primo modo di vibrare alla frequenza di 4.35 Hz;
• minuto 1:26 si attiva il secondo modo di vibrare alla frequenza di 12.35 Hz.

Clicca su play per guardare il video

Per il secondo modo di vibrare il nodo della deformata modale, di cui abbiamo parlato sopra, sarà posizionato a circa 1/3 dell’altezza dei ritti del terzo livello. Puoi vederlo nel video al minuto 1:26. Nel video manca all’appello il terzo modo di vibrare. Il terzo modo non è stato attivato perché avrebbe richiesto una frequenza di vibrazione troppo elevata e la macchina utilizzata nell’esperimento non è in grado di raggiungerla per motivi tecnici.

Dove non arrivano i test sperimentali, arriva l’analisi numerica. Ho riprodotto il modello dell’esperimento in un software di calcolo strutturale e ho lanciato un’analisi modale per ottenere il terzo modo di vibrare. Il terzo modo si attiva ad una frequenza pari a 17.06 Hz. Come ci si poteva aspettare il terzo modo ha due punti di nullo, ovvero due nodi, evidenziati in rosso nell’immagine. Ora tutto quadra ;). Eccolo qui:

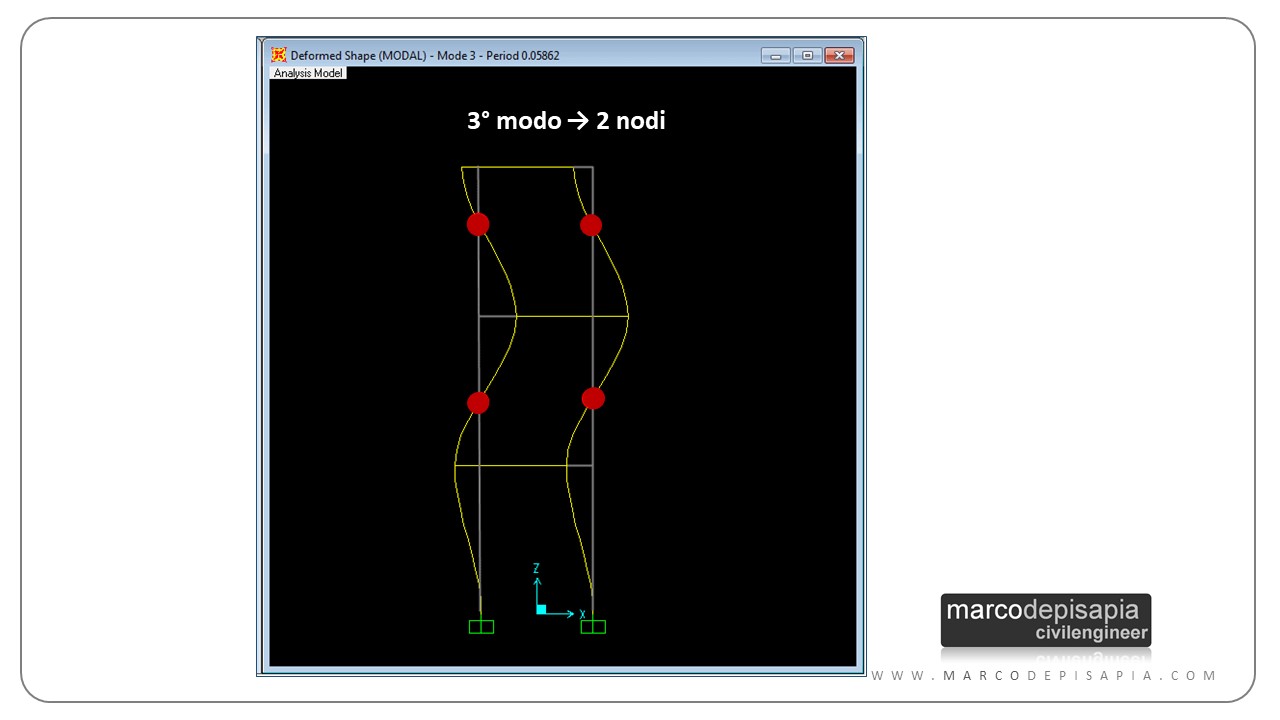
Cosa succede per le strutture tridimensionali?

Finora abbiamo considerato solo sistemi bidimensionali, liberi di oscillare nel proprio piano. Pertanto a questo punto è lecito chiedersi cosa accade per un sistema tridimensionale e da quanti gradi di libertà è caratterizzato. A tal proposito ti riporto un estratto della Normativa Tecnica NTC2018:

A meno di specifiche valutazioni e purché le aperture presenti non ne riducano significativamente la rigidezza, gli orizzontamenti piani possono essere considerati infinitamente rigidi nel loro piano medio a condizione che siano realizzati in calcestruzzo armato, oppure in latero-cemento con soletta in calcestruzzo armato di almeno 40 mm di spessore, o in struttura mista con soletta in calcestruzzo armato di almeno 50 mm di spessore collegata agli elementi strutturali in acciaio o in legno da connettori a taglio opportunamente dimensionati.

NTC2018 – par. 7.2.6

Ciascun impalcato, nella prassi tecnica, è ipotizzato infinitamente rigido nel suo piano e potrà spostarsi lungo l’asse X, lungo l’asse Y o ruotare intorno all’asse Z. Pertanto una struttura tridimensionale avrà tre gradi di libertà per ciascun piano. Esempio: una struttura di tre piani avrà un numero di gradi di libertà totale pari a: 3 piani * 3 gradi di libertà  = 9 gradi di libertà a cui corrisponderanno altrettanti 9 modi di vibrare.

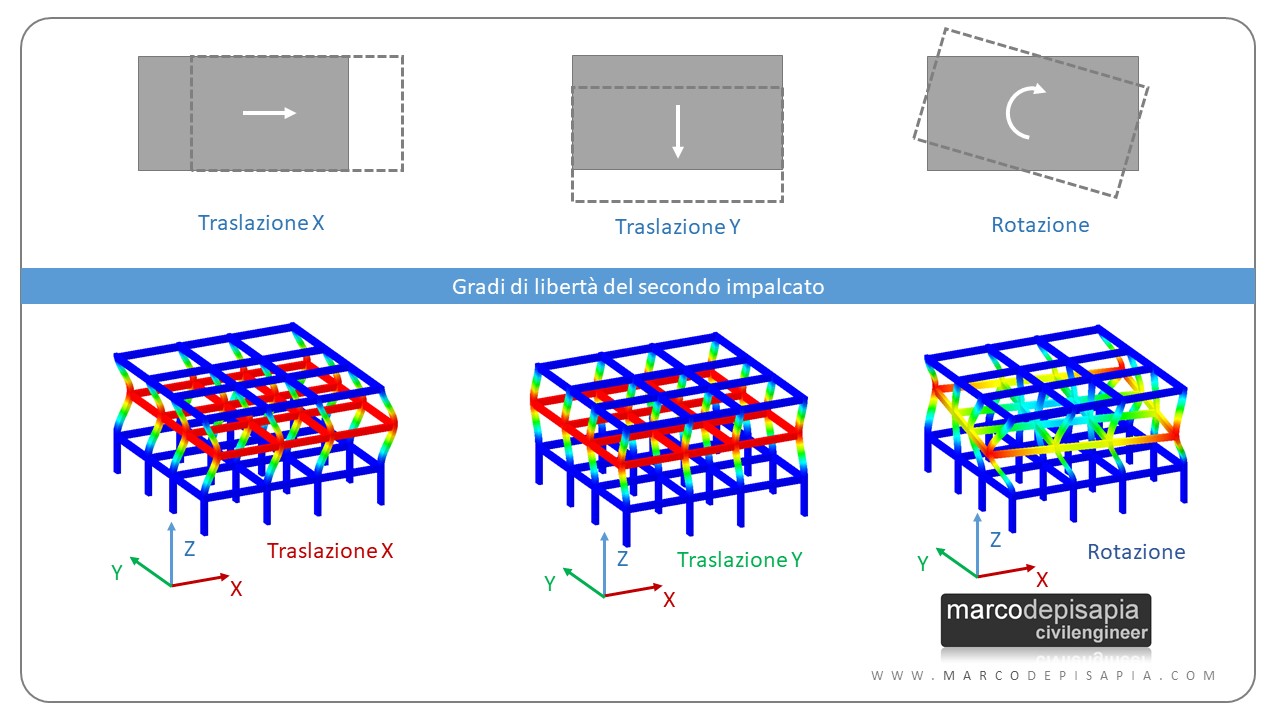
Conclusioni

L’articolo finisce qui. Spero sia stato utile per chiarire i concetti di base sui modi di vibrare di una struttura. Un progettista strutturale, oltre a saper utilizzare al meglio il proprio software di calcolo, dovrebbe avere chiari i concetti alla base delle analisi da eseguire. I software si evolveranno, saranno rilasciate continuamente nuove versioni sempre più performanti e dalla grafica più accattivante. Ciò che non cambierà sono i princìpi alla base delle analisi che i software eseguono. Per aiutarti ad essere un progettista consapevole ho creato EarthQuake, la guida pratica in PDF per l’analisi sismica delle strutture.

Puoi scaricare l’estratto gratuito di EarthQuake compilando i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download.

Noi ci aggiorniamo al prossimo articolo. Se questo post ti è piaciuto, puoi condividerlo con i tuoi colleghi su Linkedin o con i tuoi amici su Facebook cliccando sui pulsantini di condivisione social in fondo alla pagina. Ci conto ;). Se hai domande sull’argomento, puoi lasciare un commento qui sotto.

Al prossimo articolo.

Marco

---

Risorsa consigliata

Earthquake – la guida pratica per l’analisi sismica delle strutture

---

Aggiornato il 31/5/2023, pubblicato il 15/2/2016. Codice articolo: 224