Come fa un software di calcolo strutturale a risolvere qualunque schema statico dato in input? Cosa succede dopo aver cliccato sul tasto che lancia l’analisi? Configurazioni deformate e diagrammi delle sollecitazioni sembrano venir fuori come per magia. In realtà un algoritmo avanzato elabora i dati forniti in input per calcolare la soluzione del problema statico. In quest’articolo ti spiego, in 5 passaggi, come funziona l’algoritmo per il calcolo automatico delle strutture eseguito dai software di calcolo strutturale.

Conoscere i princìpi del calcolo automatico delle strutture ti aiuterà ad ottimizzare i modelli di calcolo e ad interpretare correttamente eventuali anomalie dei risultati. Alla fine dell’articolo troverai anche la versione video del contenuto e potrai scaricare Ca.Tel.2D, la risorsa gratuita per la risoluzione di schemi statici piani. Se sei un progettista strutturale e ti confronti spesso con calcoli strutturali e software di calcolo quest’articolo fa decisamente al caso tuo. Buona lettura.
I 5 passaggi del calcolo automatico delle strutture: dalla molla semplice alle strutture tridimensionali
Una molla semplice e un sistema strutturale tridimensionale sono concettualmente identici: entrambi questi sistemi hanno un comportamento elastico lineare e manifestano uno spostamento proporzionale all’intensità dei carichi applicati.
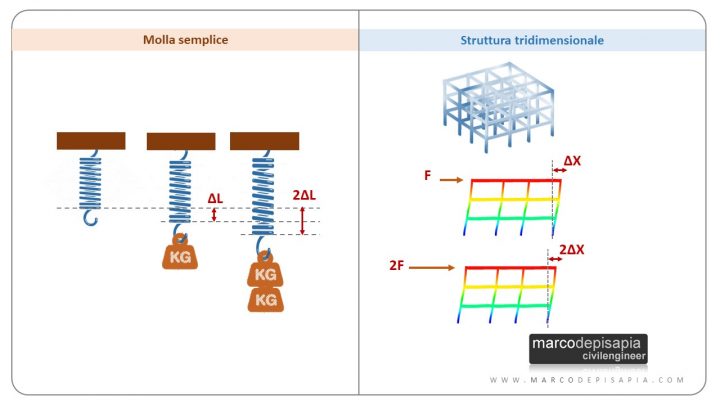
Per lo schema semplice di una molla l’unico grado di libertà è lo spostamento verticale dell’estremità. I gradi di libertà di una struttura spaziale sono invece molto più numerosi, ciascun nodo ha sei gradi di libertà nello spazio (3 traslazioni lungo gli assi X, Y e Z e tre rotazioni attorno agli assi X, Y, Z).
Il calcolo degli spostamenti incogniti di una struttura spaziale per assegnati carichi è decisamente più complesso rispetto al sistema semplice di una molla. La rigidezza di una molla è descritta da un solo parametro: la costante elastica k. Per una struttura tridimensionale invece la rigidezza è definita mediante un insieme di parametri raccolti nella matrice di rigidezza.
Il calcolo automatico delle strutture implementato negli algoritmi dei software di calcolo strutturale può essere riassunto nei 5 passaggi che trovi descritti di seguito.
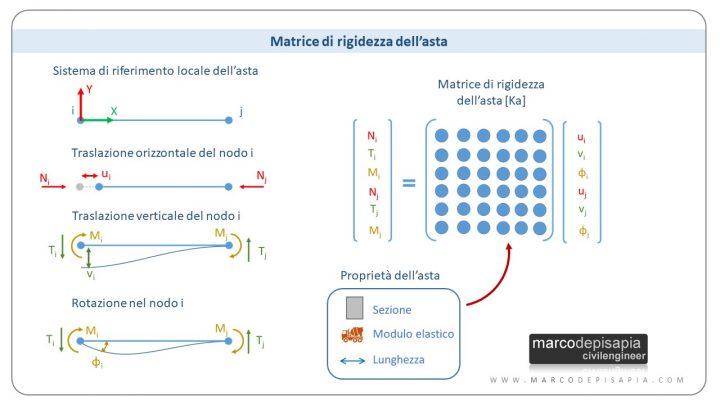
1. Calcolo automatico delle strutture: la matrice di rigidezza locale dell’asta
Ogni elemento asta di uno schema statico ha una propria matrice di rigidezza definita nel sistema di riferimento locale. La matrice di rigidezza dell’asta è una matrice quadrata e simmetrica e ha dimensione pari alla somma dei gradi di libertà di ciascun nodo di estremità:
- per uno schema statico piano ciascun nodo di estremità dell’asta avrà 3 gradi di libertà (traslazione X, traslazione Y e rotazione intorno a Z), pertanto la dimensione della matrice di rigidezza dell’asta sarà 3 g.d.l. x 2 nodi = 6, dunque una matrice 6×6;
- per uno schema statico spaziale ciascun nodo di estremità dell’asta avrà 6 gradi di libertà (3 traslazioni X,Y,Z, 3 rotazioni intorno a X,Y,Z), pertanto la dimensione della matrice di rigidezza locale sarà 6 g.d.l. x 2 nodi = 12, dunque una matrice 12×12.
I termini della matrice di rigidezza dell’asta dipendono dai seguenti parametri:
- sezione dell’asta;
- lunghezza dell’asta;
- modulo elastico del materiale.
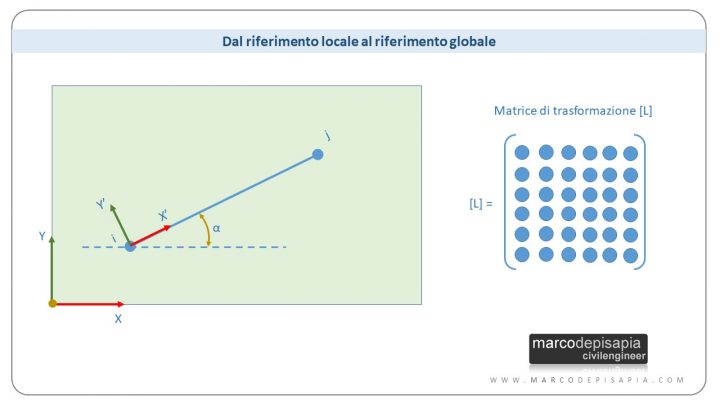
2. Dal riferimento locale al riferimento globale: la matrice di trasformazione
La matrice di rigidezza dell’asta ha validità nel sistema di riferimento locale, ovvero il sistema di riferimento con origine in un nodo dell’asta, l’asse X’ parallelo all’asse dell’asta e l’asse Y’ e Z’ ortogonali a tale asse. Per rendere valida la matrice di rigidezza dell’asta nel sistema di riferimento globale bisognerà utilizzare la matrice di trasformazione.
La matrice di trasformazione è una matrice quadrata di dimensione pari alla dimensione della matrice di rigidezza dell’asta. I termini della matrice di trasformazione sono funzione del seno e del coseno degli angoli compresi fra gli assi locali (X’,Y’,Z’) e gli assi del riferimento globale (X,Y,Z).
La matrice di rigidezza dell’asta nel riferimento globale si ottiene moltiplicando tra loro:
- la matrice di trasformazione trasposta
- la matrice di rigidezza dell’asta nel riferimento locale
- la matrice di trasformazione.
Ti riporto di seguito la formula per il calcolo:
[Ka] = [L]T [K’a] [L]
- [Ka] = matrice di rigidezza dell’asta nel riferimento globale
- [L] = matrice di trasformazione dell’asta
- [L]T = matrice trasposta della matrice di trasformazione dell’asta
- [K’a] = matrice di rigidezza dell’asta nel riferimento locale
Trasformazione della matrice di rigidezza dell’asta nel riferimento globale
3. Calcolo automatico delle strutture: assemblaggio della matrice di rigidezza globale
Il modello tridimensionale che vediamo sullo schermo dei nostri pc in realtà racchiude un insieme di numeri organizzati nella matrice di rigidezza del sistema strutturale. Vediamo come viene creata questa matrice.
Una volta note le matrici di rigidezza di tutte le aste del sistema strutturale trasformate nel riferimento globale, bisognerà assemblare le matrici di rigidezza delle singole aste per dare vita alla matrice di rigidezza globale del sistema strutturale.
La matrice di rigidezza globale del sistema strutturale sarà una matrice quadrata, simmetrica, di dimensione pari ai gradi di libertà di ciascun nodo per il numero totale dei nodi della struttura.
Esempio: in uno schema statico piano costituito da 4 nodi, la matrice di rigidezza avrà dimensione pari a 3 g.d.l. (traslazione X, Y e rotazione intorno a Z) x 4 nodi = 12. Sarà pertanto una matrice quadrata 12 x 12.
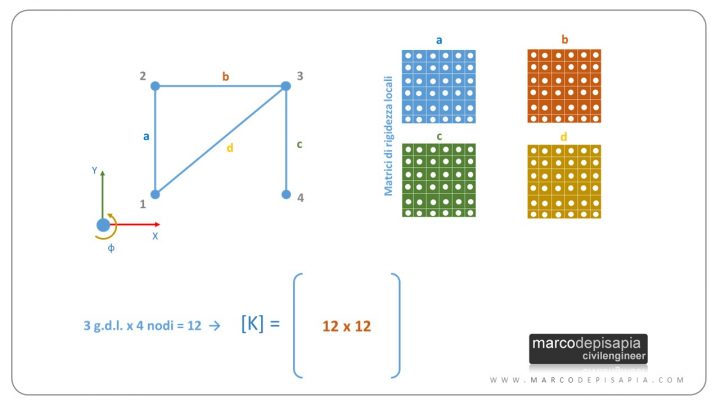
Per assemblare le matrici di rigidezza delle singole aste nella matrice di rigidezza globale bisogna considerare i nodi della struttura a cui sono connesse le singole aste. Ciascuna matrice di rigidezza dell’asta può essere suddivisa in 4 sottomatrici 3 x 3. Ogni 3 righe e 3 colonne della matrice di rigidezza globale individuano un nodo della struttura. Ciascuna sottomatrice andrà ad occupare una posizione nella matrice di rigidezza globale corrispondente ai nodi che l’asta collega.
Ti propongo un esempio per chiarire quanto appena detto. Se l’asta collega i nodi 1-3, le 4 sottomatrici della matrice di rigidezza dell’asta occuperanno gli spazi nella matrice di rigidezza globale individuati dai nodi 1 e 3, ovvero gli spazi (1,1), (1,3), (3,1), (3,3).
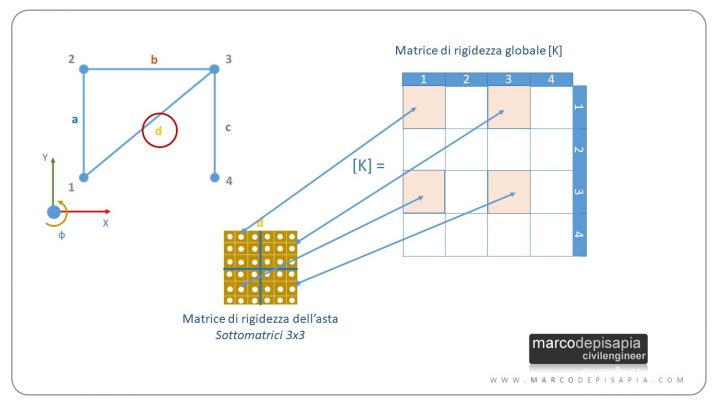
Questo procedimento viene ripetuto per tutte le aste dello schema statico. Nelle zone in cui le sottomatrici si sovrappongono, in corrispondenza dei nodi in cui convergono due o più aste, si eseguirà la somma dei singoli termini delle sottomatrici.
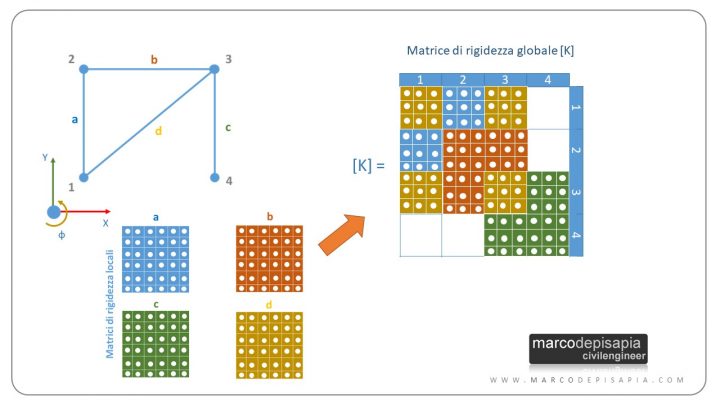
Nel video che trovi in fondo all’articolo potrai vedere, mediante un’animazione, la creazione della matrice di rigidezza globale.
In un software di calcolo strutturale quando creiamo le aste del modello connettendole ai nodi della struttura, in realtà stiamo dando istruzioni all’algoritmo di calcolo per la creazione della matrice di rigidezza globale del sistema. Quando clicchiamo sul tasto “Calcola”, l’algoritmo analizzerà tutte le connessioni delle aste ai nodi e assemblerà le matrici di rigidezza delle singole aste nella matrice di rigidezza globale.
4. Modifica della matrice di rigidezza: l’applicazione dei vincoli esterni
La matrice di rigidezza globale ottenuta dall’assemblaggio delle matrici delle singole aste non è sufficiente per ottenere la soluzione del problema statico, in quanto è rappresentativa di uno schema statico labile, per cui esistono infiniti moti rigidi. La matrice di rigidezza va modificata in funzione dei vincoli esterni applicati al modello.
Per ogni grado di libertà di un nodo soppresso da un vincolo esterno, verrà annullata la riga e la colonna corrispondente al grado di libertà di quel nodo ponendo tutti i termini pari a zero e il termine sulla diagonale principale pari a 1.
Ad esempio se nel nodo 1 viene applicato un appoggio, le traslazioni X e Y del nodo saranno impedite. Pertanto le prime due righe e le prime due colonne della matrice saranno annullate e il termine della diagonale principale sarà posto pari a 1
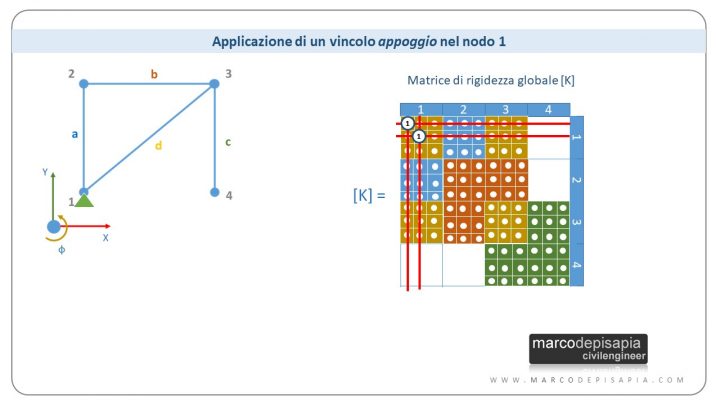
Se nel nodo 4 applichiamo un incastro, le ultime tre righe e tre colonne della matrice saranno annullate e il termine della diagonale principale sarà posto pari a 1.
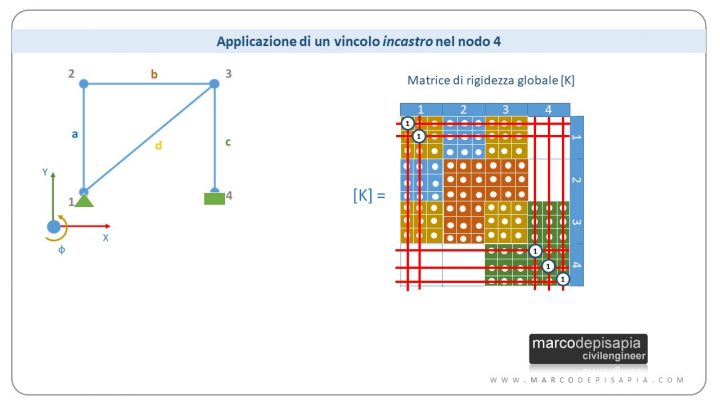
5. Calcolo automatico delle strutture: il calcolo della matrice inversa
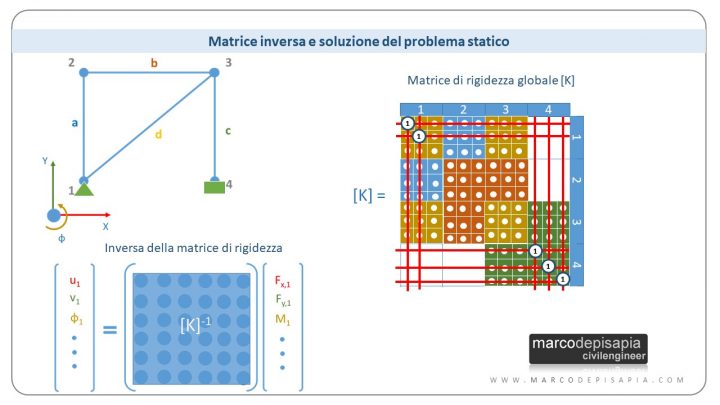
Per ottenere la soluzione del problema statico, bisognerà calcola la matrice inversa della matrice di rigidezza del sistema strutturale. L’algoritmo per il calcolo della matrice inversa è abbastanza complesso (algoritmo di Gauss-Jordan). E’ questa la fase del calcolo che richiede le maggiori risorse al processore del nostro computer, in particolar modo per modelli di calcolo di grandi dimensioni con un elevato numero di nodi (abbiamo visto infatti che la dimensione della matrice dipende dal numero di nodi dello schema statico).
Il calcolo della matrice inversa è anche una prova del nove per la corretta applicazione dei vincoli esterni ed interni. Nel caso di labilità nel nostro modello, la matrice di rigidezza non sarà invertibile ed il software mostrerà un messaggio di errore.
Soluzione del problema statico: il vettore dei carichi applicati e il calcolo degli spostamenti
Tutti i carichi esterni applicati allo schema statico vengono organizzati nel vettore dei carichi nodali. Anche i carichi distribuiti applicati alle aste vengono trasformati in forze nodali concentrate. Nel caso di un sistema piano ciascun termine del vettore colonna dei carichi corrisponde alla forza concentrata applicata in un nodo (Fx, Fy, Mz nel caso di un sistema piano) e ogni gruppo di tre termini consecutivi corrisponderà ad un singolo nodo.
Moltiplicando il vettore dei carichi nodali per l’inversa della matrice di rigidezza si otterrà il vettore degli spostamenti nodali, soluzione del problema statico.
{X} = [K]-1 {F}
- {X} = vettore degli spostamenti nodali, soluzione del problema statico
- [K]-1 = inversa della matrice di rigidezza
- {F} = vettore dei carichi nodali applicati
Nota: {…} indica un vettore, [..] indica una matrice.
Output dei risultati: sollecitazioni e spostamenti nelle singole aste
Noti gli spostamenti nodali non resta che calcolare le sollecitazioni e gli spostamenti di ciascuna asta del modello. In questo caso torna in gioco la matrice di rigidezza di ogni singola asta, scritta nel riferimento locale dell’asta.
Dal vettore degli spostamenti nodali vengono estrapolati gli spostamenti dei nodi di estremità di ciascuna asta e convertiti nel riferimento locale dell’asta mediante la matrice di trasformazione. Moltiplicando la matrice di rigidezza dell’asta per il vettore degli spostamenti nodali di estremità, si otterranno le sollecitazioni ai nodi di estremità di ogni singola asta.
{F’} = [K’a] {X’}
- {F’} = vettore delle sollecitazioni interne all’estremità dell’asta
- [K’a] = matrice di rigidezza locale dell’asta
- {X’} = vettore degli spostamenti dei nodi dell’asta nel riferimento locale
Calcolo delle sollecitazioni interne nei nodi di estremità dell’asta
Alla fine dell’esecuzione del calcolo automatico delle strutture, potremo visualizzare sul monitor tutti i risultati ottenuti:
- diagrammi delle sollecitazioni di momento flettente, taglio e sforzo normale;
- configurazione deformata con scala cromatica dei valori
- risultati in forma tabellare.
Guarda il video sul calcolo automatico delle strutture
Ho riassunto i contenuti di quest’articolo in un breve video che mostra, mediante animazioni, come funziona il calcolo automatico delle strutture. Buona visione!
Scarica Ca.Tel.2D: la risorsa per il calcolo automatico delle strutture piane

Scarica Ca.Tel.2D, la risorsa per il calcolo automatico di schemi statici piani di qualsiasi configurazione (telai, travature reticolari, capriate etc.). Compila i campi qui sotto, riceverai all’istante una mail con il link per eseguire il download.

Conclusioni: come ottimizzare il modello di calcolo
Se sei arrivato fin qui dovresti avere più chiari i passaggi che segue un software di calcolo strutturale quando diamo in input una struttura da risolvere. Dovrebbe esserti chiaro anche che, riducendo al minimo il numero di nodi necessari, si ottimizzeranno i tempi di risoluzione del modello.
Meno nodi avrà il modello, minore sarà la dimensione della matrice di rigidezza e meno tempo richiederà la risoluzione. E’ possibile quindi ottimizzare un modello di calcolo eliminando i nodi non strettamente necessari, qualora presenti, come ad esempio:
- aste divise in due o più elementi che potrebbero essere modellata come un unico elemento;
- un’eccessiva discretizzazione di elementi bidimensionali shell;
- travature reticolari che potrebbero essere modellate con elementi asta equivalenti nel modello globale.
Spero che quest’articolo ti sia stato utile. Se ti è piaciuto, puoi consigliarlo ai tuoi colleghi su Linkedin e ai tuoi amici su Facebook cliccando sui tasti di condivisione social in fondo alla pagina. Mi piacerebbe anche conoscere un tuo parere nei commenti.
Al prossimo articolo.
Marco
Risorsa consigliata sul calcolo automatico delle strutture
Libro di testo: Metodi di analisi delle strutture intelaiate di Ciro Faella
Ultimo aggiornamento: 29/11/2020. Pubblicato il 11/01/2016.


ho da leggerlo per bene
👍👍👍
Pingback:Calcolo automatico delle strutture: cosa fa il tuo software di calcolo [video]