Quando analizziamo un sistema strutturale utilizzando un modello matematico è sempre importante essere consapevoli delle ipotesi assunte alla base dell’analisi. Trascurare le ipotesi di un qualsiasi tipo di analisi può indurci a commettere degli errori e invalidare i risultati del calcolo strutturale che abbiamo ottenuto. Nel post di oggi voglio parlarti di un’ipotesi che è alla base di qualsiasi calcolo strutturale eseguito mediante un’analisi elastica lineare: l’ipotesi di piccoli spostamenti.

La maggior parte dei software di calcolo non dà nessun avviso nel caso in cui l’ipotesi di piccoli spostamenti non viene rispettata. Il software esegue comunque l’intero calcolo e tira fuori un risultato. Quasi sicuramente le verifiche non saranno soddisfatte, specie quelle allo Stato Limite di Esercizio che riguardano gli spostamenti. Ma il punto è che le sollecitazioni ottenute saranno errate se l’ipotesi di piccoli spostamenti non è rispettata.
Ti stai chiedendo perché un calcolo strutturale può perdere di significato se l’ipotesi di piccoli spostamenti non è rispettata? Continua a leggere per scoprirlo.
Ipotesi di piccoli spostamenti: se non è rispettata il tuo calcolo è carta straccia
Da bravi progettisti strutturali siamo abituati a vedere le deformazioni di un sistema strutturale attraverso i monitor dei nostri pc. Nei nostri software di calcolo possiamo amplificare a piacimento tali deformazioni per apprezzarne l’andamento. Se l’ipotesi di piccoli spostamenti non è rispettata le decine e decine di pagine dei tuoi tabulati di calcolo rischiano di diventare carta straccia.
Che vuol dire piccoli spostamenti? Se ci pensi viviamo in un mondo di strutture deformate. Le strutture che ci circondano si trovano tutte nella loro configurazione deformata per effetto del peso proprio, dei carichi permanenti e dei carichi accidentali agenti. Il solaio sopra la tua testa è deformato, così come quello su cui ti trovi adesso mentre stai leggendo quest’articolo.
Un osservatore che guarda una struttura ad occhio nudo non sarà in grado distinguere fra la configurazione deformata e la configurazione indeformata, a meno che la struttura non si sia danneggiata in campo plastico per effetto delle azioni orizzontali prodotte da un evento sismico per esempio.
Per capire perché l’ipotesi di piccoli spostamenti è cosi importante ai fini della validità dell’analisi elastica lineare di una struttura bisogna riportare alla memoria l’equazione della linea elastica. Non sono solito pubblicare formule o dimostrazioni di teoremi qui sul blog, in genere preferisco dare un taglio pratico ai post. In quest’articolo si rende necessaria un’eccezione.
Per risolvere il problema elastico di una trave bisogna risolvere l’equazione della linea elastica. Quest’equazione mette in relazione la funzione y(x) della deformata dell’asse della trave con il carico distribuito q applicato lungo l’asta. Te la riporto di seguito:
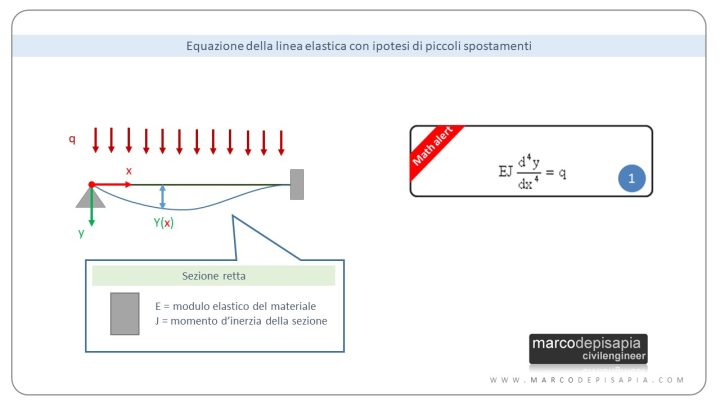
Integrando quattro volte quest’equazione ed imponendo le corrette condizioni al contorno a seconda dei vincoli esterni applicati ai nodi di estremità, è possibile risolvere il problema elastico della trave e ottenere spostamenti e sollecitazioni. Per un veloce ripasso sull’equazione della linea elastica ti suggerisco quest’articolo del blog, all’interno del quale potrai scaricare il Focus Analitico PDF che riporta tutti i passaggi matematici necessari per ottenere l’equazione della linea elastica.
Equazione della linea elastica: forma completa e forma semplificata
L’equazione della linea elastica riportata nell’immagine sopra è un’espressione semplificata della sua forma completa. La semplificazione deriva proprio dalla validità dell’ipotesi di piccoli spostamenti. L’equazione della linea elastica, se l’ipotesi di piccoli spostamenti venisse rimossa, sarebbe la seguente:
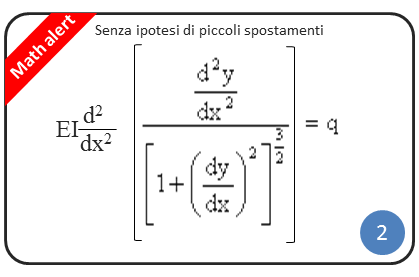
Nel caso di validità dell’ipotesi di piccoli spostamenti, la derivata prima dy/dx della funzione spostamento y(x) a denominatore, elevata al quadrato, diventa trascurabile. Elidendo tale termine si ottiene l’equazione della linea elastica nella sua forma semplificata.
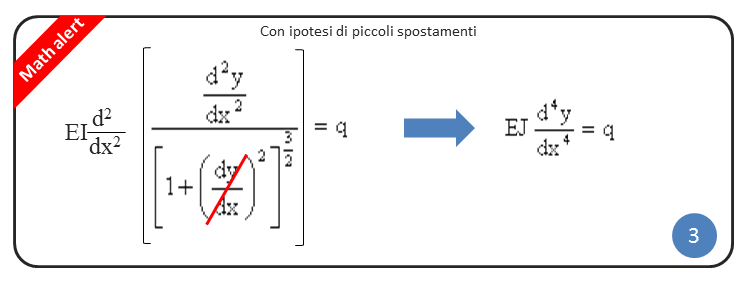
Come puoi vedere dalle formule riportate sopra, integrare l’equazione (2) sarebbe senz’altro più complesso. Inoltre i software di calcolo strutturale non sono in grado di risolvere l’equazione (2). L’algoritmo dei software di calcolo, nella maggior parte dei casi, è stato creato assumendo l’ipotesi di piccoli spostamenti. Pertanto se gli spostamenti del tuo modello non sono effettivamente piccoli, il tuo calcolo perde di validità.
Farà eccezione il caso in cui il tuo software di calcolo sia in grado di eseguire analisi del secondo ordine o del terzo ordine, portando in conto le non linearità geometriche che rimuovono l’ipotesi di piccoli spostamenti. Ma si tratta di analisi avanzate che vengono utilizzate in casi particolari.
Ipotesi di piccoli spostamenti: come evitare un calcolo iterativo
Per effetto dell’ipotesi di piccoli spostamenti le sollecitazioni negli elementi strutturali vengono calcolate considerando i carichi agenti sulla struttura nella sua configurazione indeformata. Cosa vuol dire?
Te lo spiego meglio con un esempio. Ho creato un modello di esempio utilizzando Ca.Tel.2D, l’applicazione del blog per la risoluzione di schemi statici piani. Se non l’hai ancora scaricata, puoi farlo a questo link. Il modello di esempio che ti propongo è costituito da un’asta verticale incastrata alla base ed un’asta orizzontale, con una forza concentrata verticale applicata nel nodo di estremità dell’asta orizzontale (nodo 3 nel modello). Puoi vedere il modello di calcolo nell’immagine seguente.
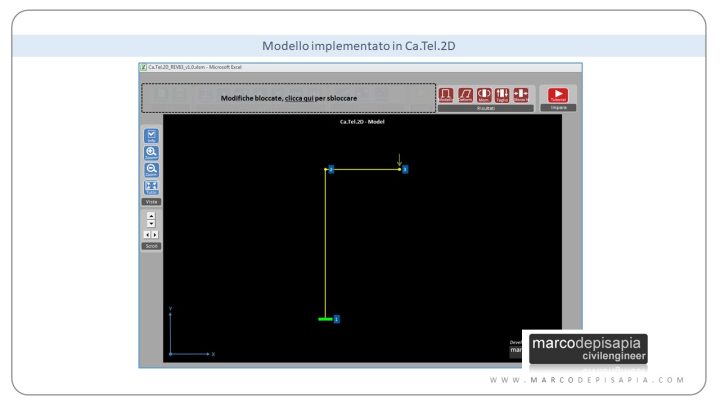
Nella configurazione deformata, il punto di applicazione della forza concentrata subirà uno spostamento sia verticale che orizzontale. Per effetto dello spostamento orizzontale del nodo 3 (all’estremità destra dell’asta orizzontale), aumenterà il braccio della forza verticale rispetto all’incastro di base del sistema e di conseguenza aumenterà il momento sollecitante nell’asta verticale.
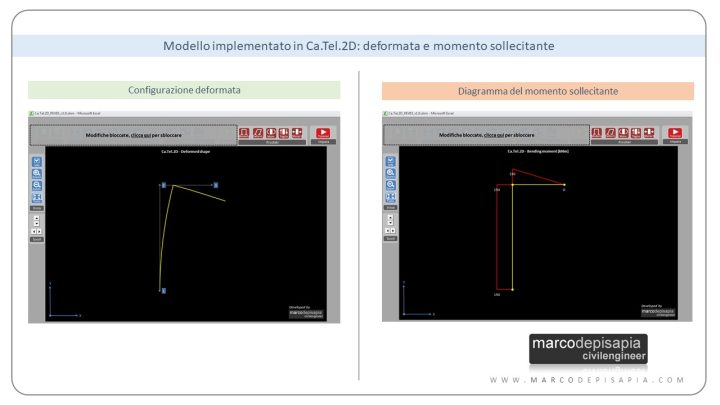
Aumentando il braccio della forza, aumenterà il momento sollecitante nell’asta verticale e di conseguenza la sua deformazione flessionale e lo spostamento orizzontale del nodo 3. Per ottenere la soluzione del problema statico in tal caso, considerando la forza applicata nella configurazione deformata del sistema, bisognerebbe eseguire un calcolo iterativo finché l’incremento di sollecitazioni non diventi trascurabile rispetto al valore del momento flettente dell’iterazione precedente. Trovi la schematizzazione del procedimento iterativo nell’immagine seguente.
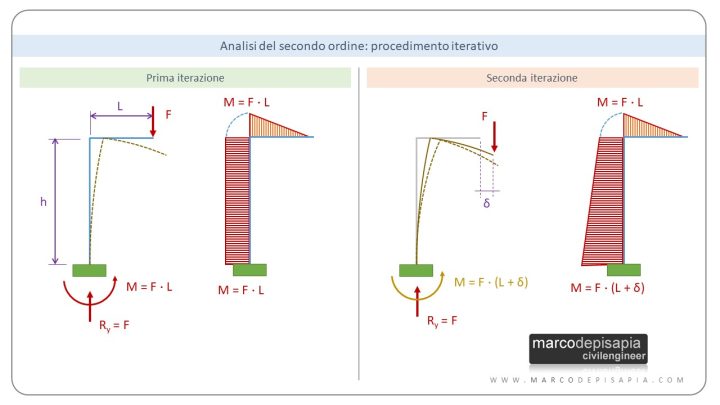
La validità dell’ipotesi di piccoli spostamenti ci assicura che l’errore commesso considerando le forze agenti nella configurazione indeformata del sistema strutturale sia trascurabile, evitandoci in tal modo di dover eseguire un calcolo iterativo. Le sollecitazioni ottenute saranno quelle calcolate considerando i carichi agenti nella configurazione indeformata del sistema.
Ipotesi di piccoli spostamenti: ma piccoli quanto?
I testi scientifici di scienza e tecnica delle costruzioni, nel citare l’ipotesi di piccoli spostamenti, solitamente non specificano quanto devono essere piccoli questi spostamenti. Che vuol dire piccoli spostamenti? Piccoli quanto? Possiamo provare a rispondere a questa domanda con un esempio pratico.
L’ipotesi di piccoli spostamenti fa si che sia possibile confondere l’angolo di rotazione, espresso in radianti, della sezione di una trave nella configurazione deformata con la tangente di tale angolo e di conseguenza con la derivata prima della funzione spostamento, calcolata nel punto corrispondente dell’asse della trave.
Il valore limite della rotazione della sezione per far sì che sia possibile confondere l’angolo con la sua tangente e di conseguenza con la derivata prima dello spostamento, considerando tre cifre decimali, è pari a 0.114 radianti, ovvero pari a 6.53°. Ti riporto un esempio creato con Ca.Tel.2D. Consideriamo lo schema di una trave appoggiata-appoggiata con una forza concentrata in mezzeria e una luce di 6 metri. Qual è lo spostamento massimo in mezzeria per far si che l’ipotesi di piccoli spostamenti sia soddisfatta?
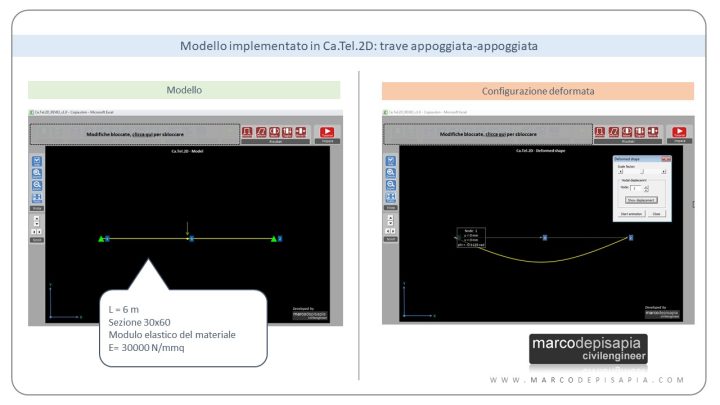
La rotazione massima che possiamo avere alla sezione di estremità in corrispondenza dell’appoggio è pari a phi = 0.114 rad; la tangente di phi sarà anch’essa pari a 0.114. A tale rotazione di estremità corrisponde uno spostamento in mezzeria pari a 228 mm.
Rapportando tale spostamento alla lunghezza della trave, possiamo dire che, per una trave appoggiata-appoggiata di lunghezza 6 metri, l’ipotesi di piccoli spostamenti è soddisfatta se l’abbassamento in mezzeria non supera all’incirca 1/26 della lunghezza della trave.
Conclusioni
L’argomento del post di oggi è un po’ più tecnico del solito. E’ stato necessario richiamare alla memoria equazioni della linea elastica, derivate prime e tipologie di analisi. Il messaggio che vorrei trasmetterti è che i software di calcolo automatizzano le procedure, ma è compito del progettista accertarsi che il calcolo sia valido e che tutte le ipotesi alla base dell’analisi siano rispettate. Per far ciò bisogna avere consapevolezza di ciò che si sta facendo in modo da essere in grado di valutare i risultati con spirito critico.
Spero tu abbia trovato utile il contenuto del post di oggi. Se ti è piaciuto puoi suggerirlo ai tuoi colleghi su Linkedin o ai tuoi amici su Facebook cliccando sui tasti di condivisione social che trovi in fondo alla pagina. Ti eri mai soffermato a riflettere sull’importanza dell’ipotesi di piccoli spostamenti? Puoi farmelo sapere lasciando un commento al post.
Al prossimo articolo.
Marco
Ultimo aggiornamento: 21/2/2023. Pubblicato il 20/3/2017. Codice articolo: 219

Se ho ben capito allora significa che se contengo gli abbassamenti reali di una trave o di un solaio in L/260 sono sempre almeno sicuro di essere nell’ipotesi di piccoli spostamenti o sbaglio?.
Grazie anticipate per la risposta.
Esatto. Dai risultati ottenuti dall’esempio, 1/26 della luce.
Ciao
Marco