La fase finale di un calcolo strutturale richiede la verifica della fondazione. Dopo aver analizzato la struttura in elevazione, calcolato le sollecitazioni, dimensionato gli elementi e le armature si passa alla verifica delle strutture di fondazione. In questo articolo voglio parlarti dell’interazione terreno-fondazione e di come viene modellato il terreno per calcolare le sollecitazioni negli elementi in fondazione. Per interazione terreno-fondazione si intendono gli effetti reciproci che le deformazioni della fondazione e i cedimenti del terreno hanno l’uno sull’altro.

Scarica l’app Plate Design (xls di Microsoft Excel) per la verifica strutturale e geotecnica di una fondazione a platea

Plate Design è l’app per il progetto e verifica di fondazioni a platea in calcestruzzo armato implementata in Microsoft Excel. Puoi scaricare la versione gratuita dell’app compilando i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download.

Esistono due modi di operare quando si esegue il calcolo di una struttura:
- considerare la struttura incastrata alla base per poi procedere in un secondo momento alla verifica della fondazione trasferendo alla struttura di fondazione le reazioni vincolari di base
- considerare un modello completo della nostra struttura, composto dalla fondazione e dal terreno (se il software di calcolo che utilizziamo ce lo permette)
Indipendentemente dall’approccio scelto, il modello più diffuso per riprodurre il comportamento del terreno è il modello di suolo alla Winkler.
Il modello di Winkler considera il suolo costituito da un letto di molle indipendenti fra loro con comportamento elastico e rigidezza caratteristica k espressa come una forza su una dimensione al cubo [F/L^3]. Lo spostamento verticale di ciascun punto del terreno di fondazione dipende dalla pressione agente in quel punto. Questo modello è alquanto semplice ed è anche il più diffuso per il calcolo delle sollecitazioni nella struttura di fondazione.
L’approssimazione del modello di suolo alla Winkler

Il modello di suolo alla Winkler presenta una differenza rispetto alla realtà. Il suolo alla Winkler essendo modellato come un letto di molle indipendenti fra loro, non è in grado di riprodurre la diffusione delle tensioni al di fuori dell’area di impronta della fondazione. Il cedimento sarà localizzato solamente al di sotto dell’area della fondazione, mentre il resto del suolo resterà indeformato nella sua configurazione iniziale.
Nella realtà invece il suolo immediatamente adiacente ai bordi della fondazione presenterà un abbassamento, dovuto alla diffusione delle tensioni al di fuori dell’area di impronta della fondazione. Ti puoi subito rendere conto della differenza nell’immagine qui sotto.
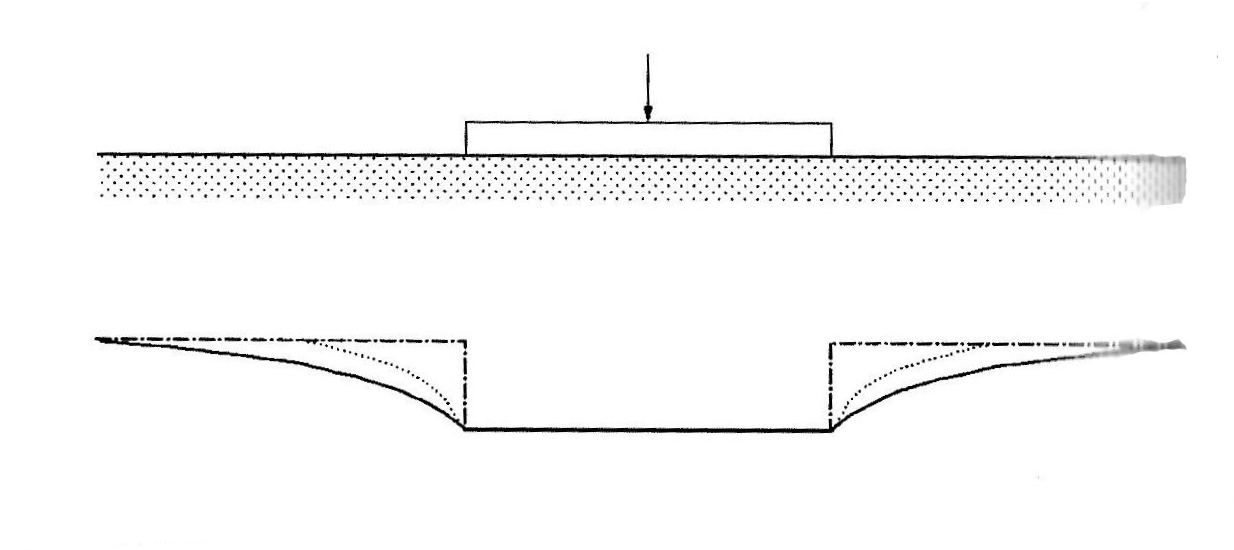
Puoi vedere un confronto fra il cedimento ottenuto con il metodo di Winkler (linea tratto-punto) e il cedimento reale del terreno (linea punteggiata) per una fondazione infinitamente rigida con un carico verticale applicato in mezzeria. Come puoi vedere nel modello di suolo alla Winkler il terreno adiacente alla fondazione non risente della presenza del carico.
Come determinare il k di Winkler?

Il valore da attribuire al k di Winkler non è di immediata determinazione. Il k di Winkler è espressione del modello geotecnico di sottosuolo. Non sarebbe corretto estrapolarlo da una tabella come proposto in alcuni manuali, soprattutto se il sottosuolo non è omogeneo.
In un terreno reale il cedimento dipende oltre che dalle proprietà dei diversi strati di sottosuolo e dal valore dei carichi applicati, anche dalla forma e dimensione della fondazione e dalla costituzione del sottosuolo.
Il metodo più corretto per ottenere il k di Winkler sarebbe quello di calcolare questo parametro come il rapporto fra il carico applicato e il cedimento w ottenuto utilizzando un metodo di calcolo appropriato e tutte le informazioni ottenute dalle indagini geotecniche.
In caso di sottosuolo omogeneo si possono utilizzare due semplici metodi per ottenere il k di Winkler:
- k = Eed / B in cui: Eed è il modulo edometrico del terreno e B è la larghezza della fondazione.
- Ricorrere al valore di k1 determinato con prove di carico su piastre standard di dimensione 30×30 cm. Il valore di k1 si può trovare tabellato per diversi tipi di terreno; questo valore va poi convertito attraverso le formule che ti riporto sotto per tenere conto della dimensione reale della fondazione.
k = k1 (b / 1.5B ) per terreni a grana fine (argilla e limo)
k = k1 [ (B+b) / 2b ] ^2 per terreni a grana grossa (sabbie)
in cui b = 30 cm è la dimensione della piastra standard di prova; B = larghezza della fondazione
C. Viggiani – Fondazioni
La soluzione per una trave di fondazione
Per calcolare le sollecitazioni per una trave di fondazione abbiamo a disposizione una soluzione analitica ottenuta risolvendo le equzioni caratteristiche del problema. Si tratta di un problema di trave elastica su suolo elastico. Sono disponibili nella letteratura tecnica delle soluzioni per diverse configurazioni di vincoli e di carichi. In tal modo è possibile ottenere gli spostamenti e le sollecitazioni utilizzando le soluzioni tabellari e senza l’ausilio di alcun software. In fase di predimensionamento possiamo quindi eseguire manualmente (magari con l’aiuto di un foglio elettronico) i nostri calcoli.
Che succede per una platea di fondazione?
Risolvere il problema per un elemento strutturale non più mono-dimensionale come una trave di fondazione, ma bidimensionale come una piastra è più complesso e non esistono soluzioni esatte disponibili (formule analitiche o risultati tabellari) a meno che non si tratti di un caso particolare come quello di una piastra circolare. Per il caso di piastra circolare su suolo elastico esiste una soluzione esatta disponibile, utile se si sta verificando la fondazione circolare di un silos.
Nel caso di piastra rettangolare bisogna ricorrere a metodi numerici per ottenere la soluzione del problema. Non è pensabile ottenere tale soluzione manualmente, ma c’è bisogno di un programma di calcolo che implementi uno dei metodi disponibili per la risoluzione.
I metodi di risoluzione per elementi bidimensionali
Esistono diversi metodi di risoluzione per il calcolo di elementi bidimensionali:
- Metodi di risoluzione agli Elementi Finiti
- Metodo delle Differenze Finite (è il metodo utilizzato in quest’applicazione del blog)
- Metodi approssimati (Grashov o metodo delle strisce)
Un metodo di risoluzione che si presta molto bene ad essere implementato in un foglio elettronico è il metodo delle Differenze Finite. Il metodo delle differenze finite consiste nel discretizzare la piastra in un reticolo di dimensioni MxN. Per ciascun punto del reticolo le equazioni differenziali del problema vengono scritte in termini di differenze finite. E’ il metodo di risoluzione su cui si basa l’applicazione disponibile sul blog per il calcolo di una platea di fondazione: Plate Design.
Conclusioni
Come abbiamo visto l’interazione terreno-fondazione è alla base del calcolo delle sollecitazioni negli elementi di fondazione. Una piccola nota prima di lasciarci: ricorda che il modello di suolo alla Winkler è da utilizzare solo per il calcolo delle sollecitazioni, ma non per il calcolo dei cedimenti della struttura. Il calcolo dei cedimenti richiede dei metodi ad hoc a seconda del tipo di sottosuolo e del grado di accuratezza che si vuole raggiungere. Esistono diversi metodi disponibili per il calcolo dei cedimenti a seconda del tipo di sottosuolo.
Spero che quest’articolo ti sia stato utile. Se vuoi consigliarlo a qualche amico o collega utilizza i tasti social in fondo alla pagina. Se sei arrivato fin qui è probabile che la progettazione geotecnica faccia parte delle tue competenze. E tu che metodo utilizzi quando devi dimensionare una platea di fondazione? Puoi farmelo sapere lasciando un commento qui sotto.
Al prossimo articolo
Marco
