Il solaio in laterocemento è il primo elemento strutturale oggetto di progettazione e calcolo per la realizzazione di una nuova costruzione o per l’analisi di una costruzione esistente. E’ l’elemento orizzontale che trasferisce il carico verticale alle travi della struttura e la prima tappa nel percorso che seguono i carichi verticali per scaricare in fondazione.
Il solaio in laterocemento viene calcolato utilizzando lo schema statico di trave continua. L’implementazione delle combinazioni di carico da considerare presenta però una particolarità: al fine di massimizzare le sollecitazioni bisognerà adoperare delle combinazioni di carico a scacchiera. Ma cosa sono e come si ottengono?

In quest’articolo ti spiego come creare le combinazioni di carico a scacchiera per massimizzare le sollecitazioni di momento e taglio nello schema di trave continua del solaio in laterocemento. Nel corso dell’articolo potrai scaricare un’applicazione che ti consentirà di calcolare in automatico le sollecitazioni massime nella trave continua, di eseguire il progetto dei ferri di armatura e della fascia piena e semipiena del solaio e la verifica per flessione e taglio.
Scarica Ver.Sez. (xls di Microsoft Excel) per il calcolo dello schema di trave continua di un solaio latero-cementizio

Ver.Sez. è l’app per il calcolo dello schema di trave continua di un solaio latero-cementizio e per il progetto e verifica dei ferri di armatura dei travetti implementata in Microsoft Excel. Puoi scaricare la versione gratuita dell’app compilando i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download.

Solaio in laterocemento: tecnologia costruttiva e schema statico
L’abbondante produzione di laterizi in Italia ha reso il solaio in laterocemento la tecnologia costruttiva più diffusa per la realizzazione di orizzontamenti, di gran lunga preferita ai solai a piastra a soletta piena largamente utilizzati nel Nord Europa.
Un solaio in laterocemento è composto da travetti in calcestruzzo armato, disposti ad interasse costante, fra i quali vengono collocati elementi di alleggerimento con funzione non portante come blocchi in laterizio (anche detti pignatte) e da una soletta in calcestruzzo, in genere di spessore 4 cm, in cui è annegata una rete elettrosaldata.
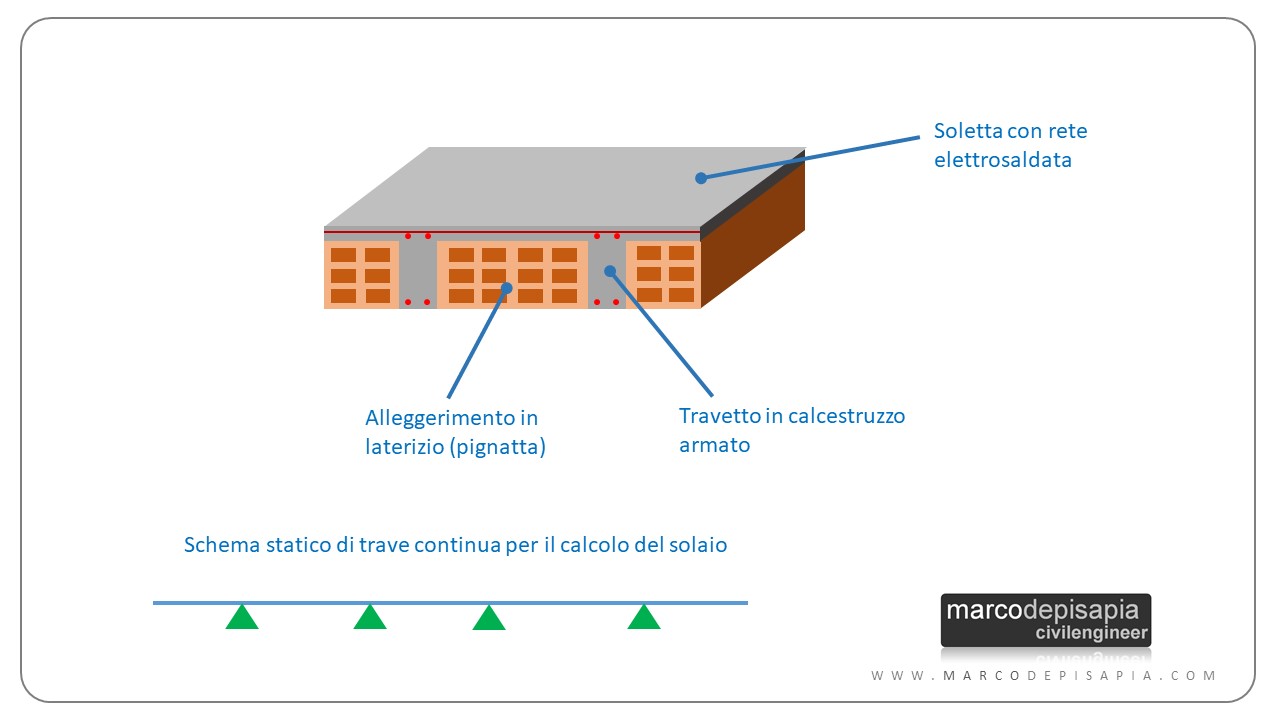
A differenza di un solaio a piastra che ripartisce i carichi in tutte le direzioni, i solai laterocementizi sono solai monodirezionali, ovvero trasmettono il carico verticale nella direzione di orditura, coincidente con la direzione dei travetti. Il modello statico adottato per il calcolo e verifica di un solaio laterocementizio è lo schema di trave continua su più appoggi. Gli appoggi della trave continua rappresentano le travi dell’impalcato su cui il solaio scarica.
Solaio in laterocemento: come massimizzare le sollecitazioni
Per garantire la massima sicurezza dei solai in laterocemento nei confronti dei carichi verticali è fondamentale considerare le combinazioni di carico a scacchiera. Le combinazioni di carico a scacchiera hanno lo scopo di massimizzare le sollecitazioni nella trave continua con cui si schematizza il solaio. L’obiettivo è ottenere i seguenti risultati:
- massimizzazione del momento sollecitante in campata, per ogni campata della trave continua;
- massimizzazione del momento sollecitante all’appoggio, per ogni appoggio della trave continua;
Come massimizzare il momento in campata
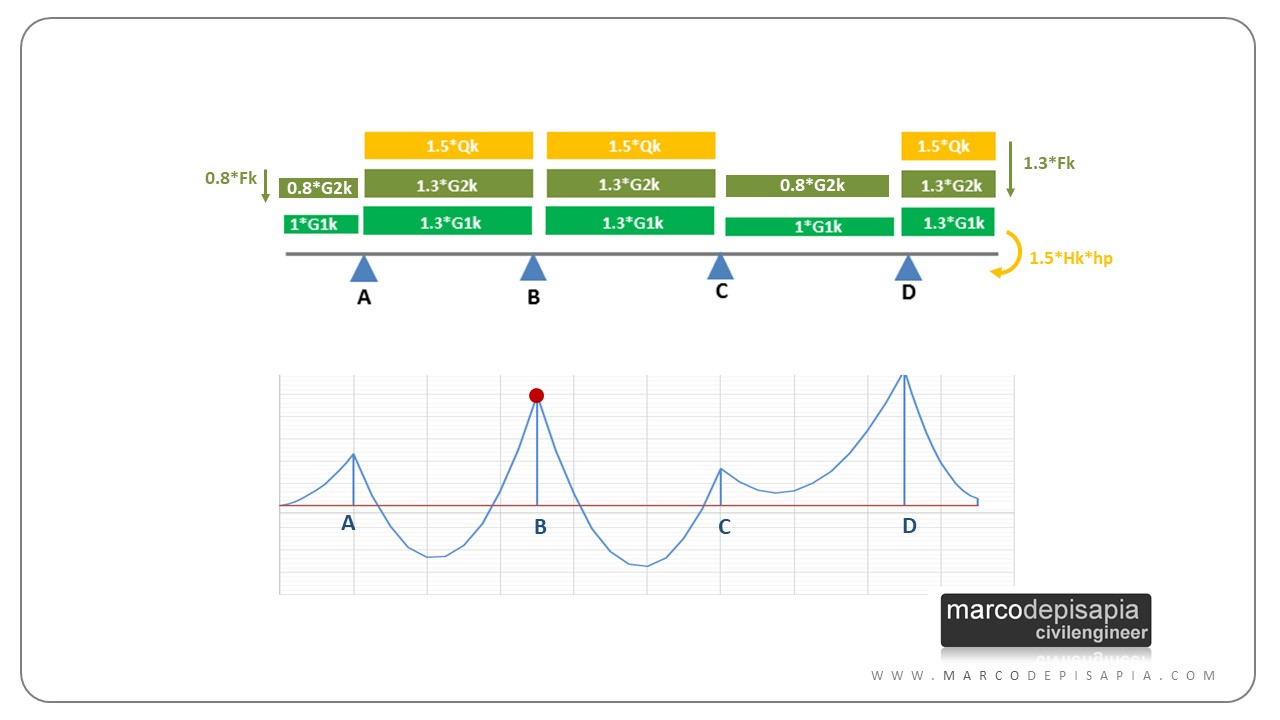
Per ottenere la massimizzazione del momento flettente in campata bisogna caricare la campata in cui si vuole massimizzare il momento e lasciare scariche le campate immediatamente adiacenti a sinistra e a destra. Le restanti campate della trave continua vanno caricate in maniera alternata, secondo una distribuzione di carichi a scacchiera per l’appunto.
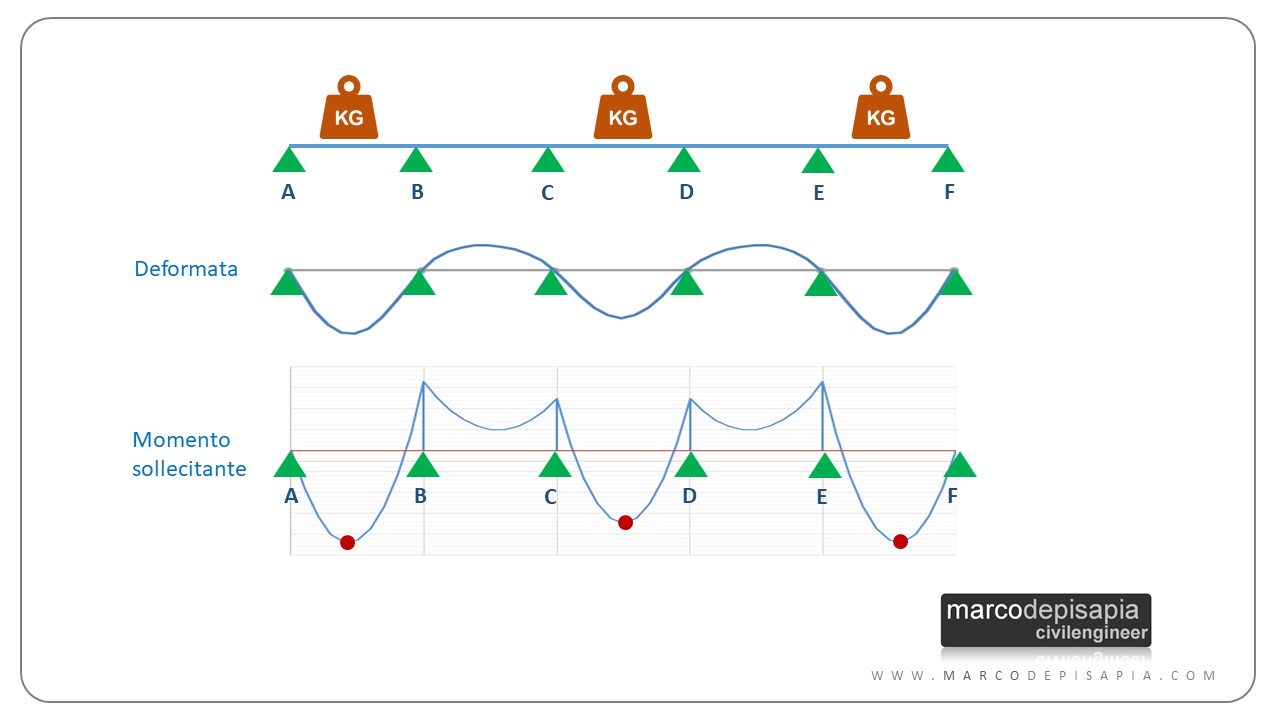
Come massimizzare il momento all’appoggio
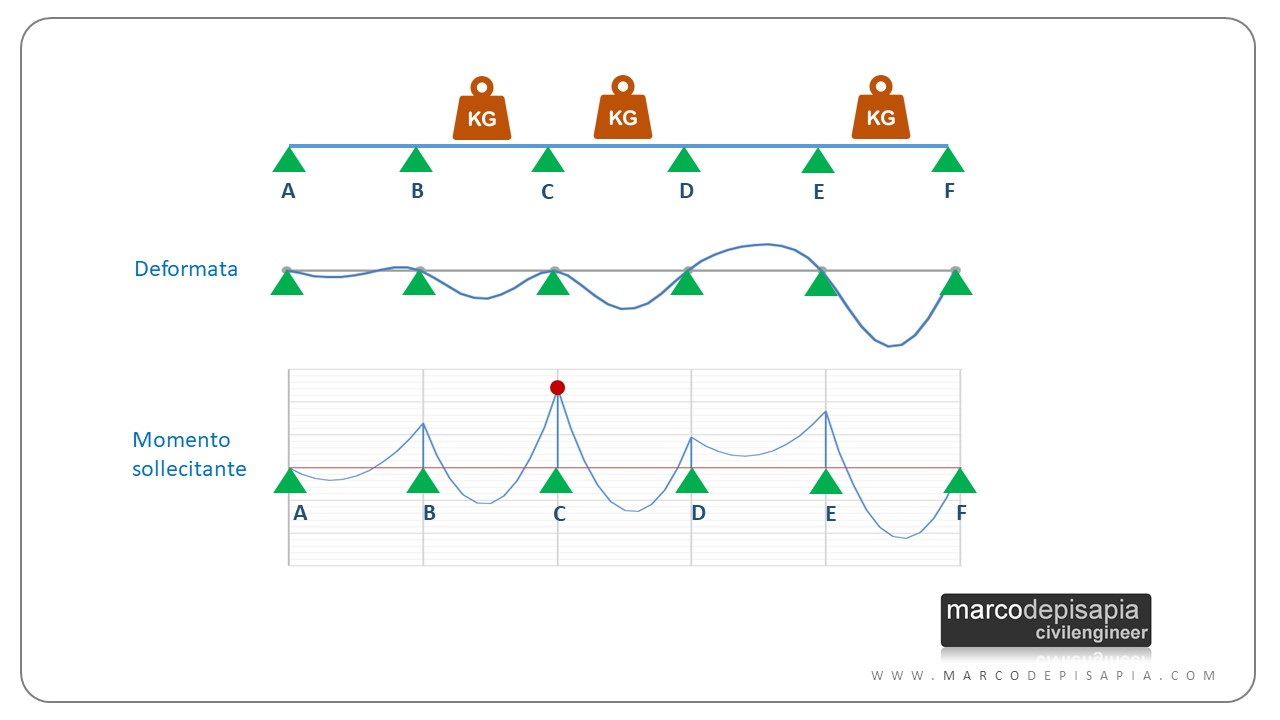
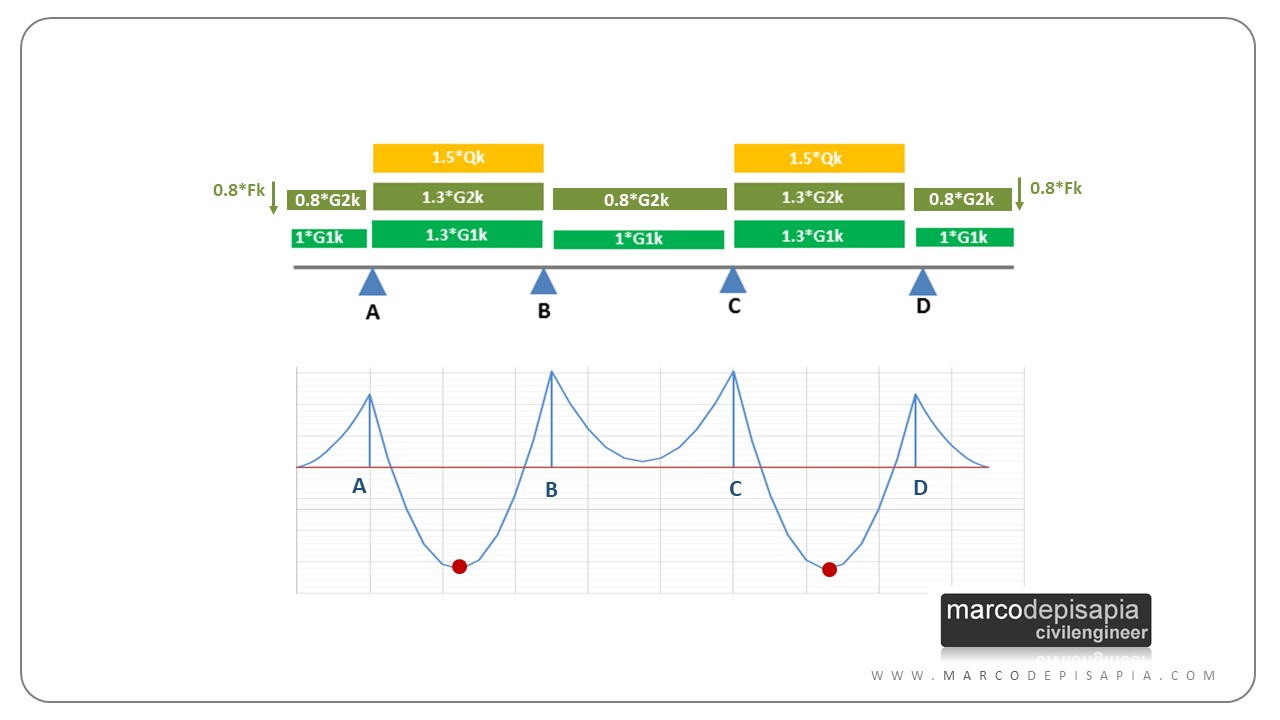
Per massimizzare il momento sollecitante in corrispondenza di un appoggio, bisogna caricare entrambe le campate ai lati dell’appoggio e lasciare scariche le altre due campate immediatamente adiacenti a sinistra e a destra delle campate caricate. Le restanti campate della trave continua vanno caricate in maniera alternata secondo una distribuzione di carichi a scacchiera.
Solaio in laterocemento: un esempio numerico in Ca.Tel.2D
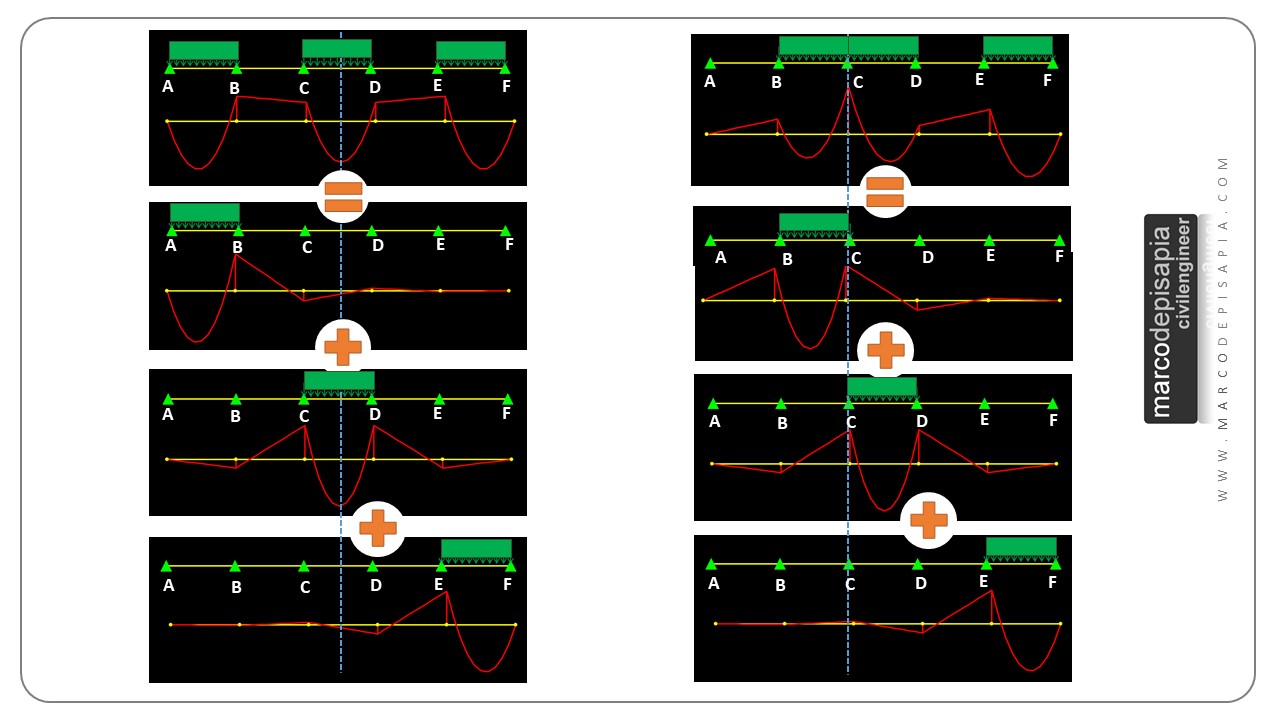
Le combinazioni di carico a scacchiera consentono di avere, per ogni condizione di carico della singola campata, un contributo dello stesso segno della sollecitazione che si vuole massimizzare, in un assegnato punto della trave continua: mezzeria di una campata o all’appoggio.
Nell’immagine di seguito ti mostro un esempio numerico implementato in Ca.Tel.2D in cui sono state implementate le condizioni di carico per le singole campate. Il contributo delle singole condizioni di carico viene sommato per ottenere la massimizzazione del momento nella campata centrale o nell’appoggio C.
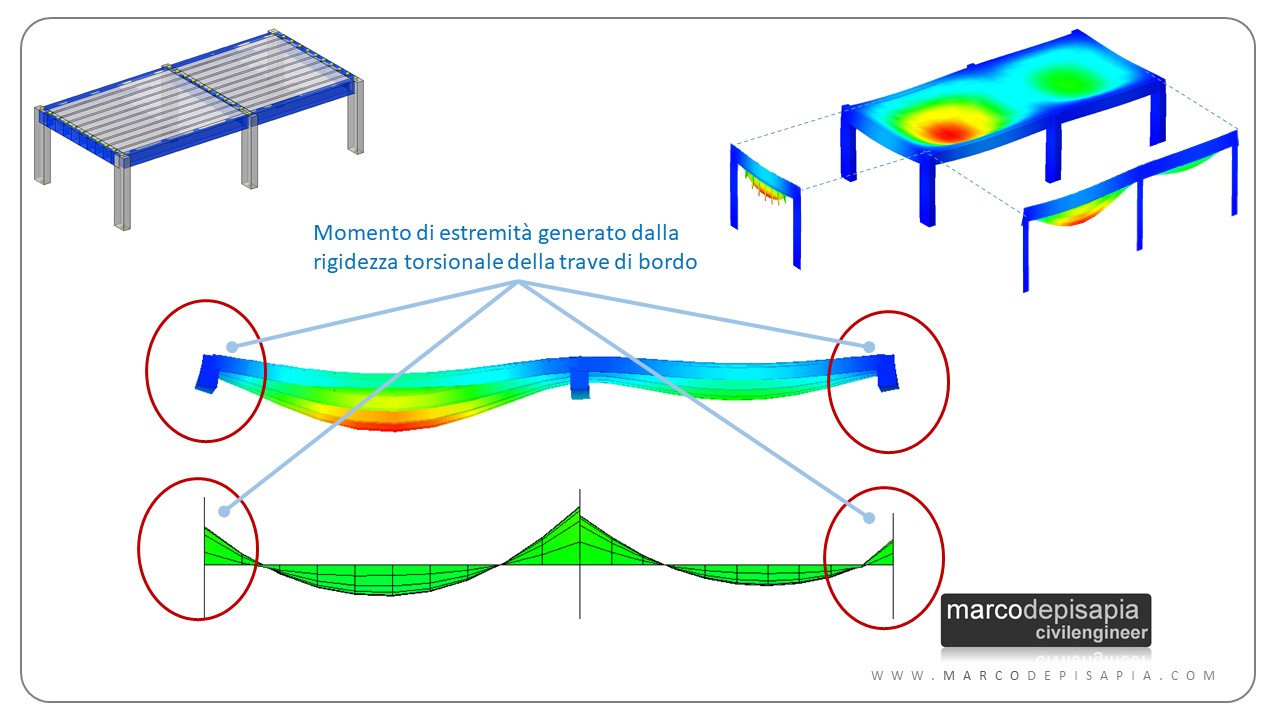
Assenza di sbalzo: il momento fittizio di estremità
In assenza di sbalzi, lo schema di trave continua presenta un limite per gli appoggi di estremità. In tali appoggi la schematizzazione a cerniera trascura completamente la rigidezza torsionale della trave di bordo. La trave di bordo crea un vincolo cedevole elasticamente nei confronti della rotazione di estremità della trave continua. In tali appoggi si ha di fatto un momento flettente negativo che nello schema di trave continua risulterà essere nullo.
Per tenere conto della rigidezza torsionale della trave di bordo, è possibile correggere il diagramma del momento flettente inserendo un momento negativo fittizio all’estremità, pari ad un momento di semi-incastro, ovvero pari a:
M = q ⋅ L2 / 24
- q = carico uniformemente distribuito in campata.
- L = luce della campata;
- M = momento di semi-incastro;
Formula per il calcolo del momento di semi-incastro
Ti mostro nell’immagine seguente l’effetto della rigidezza torsionale della trave di bordo sul momento di estremità della trave continua. Modellando i travetti del solaio mediante elementi asta di sezione 10×22 cm e la soletta mediante un elemento shell di spessore 4 cm in un software di calcolo strutturale ad elementi finiti è possibile riprodurre fedelmente il comportamento statico del solaio.
Solaio in laterocemento: quante combinazioni considerare
Le combinazioni di carico a scacchiera generano un diverso diagramma del momento per ogni combinazione. Ma quante combinazioni di carico bisogna considerare in funzione del numero di campate del solaio?
Nell’ipotesi di trave continua con sbalzi a sinistra e a destra vale la seguente formula:
numero max di combinazioni a scacchiera = 2 x numero di campate + 1
- 1 campata -> 3 combinazioni;
- 2 campate -> 5 combinazioni;
- 3 campate -> 7 combinazioni;
- e così via…
I coefficienti parziali di sicurezza per le combinazioni di carico a scacchiera
Le combinazioni di carico a scacchiera, per lo schema di trave continua, possono essere ottenute nella pratica tecnica utilizzando i coefficienti parziali di sicurezza proposti dalla Normativa Tecnica NTC2018. Sfruttando la differenziazione dei coefficienti parziali per condizioni favorevoli all’equilibrio e sfavorevoli all’equilibrio, è possibile creare le combinazioni di carico a scacchiera per il solaio al fine di massimizzarne le sollecitazioni.
I carichi favorevoli all’equilibrio determinano una riduzione delle sollecitazioni. Per questo tipo di carichi la Normativa Tecnica propone i seguenti coefficienti parziali:
- γG1 = 1 per i carichi permanenti strutturali;
- γG2 = 0.8 per i carichi permanenti non strutturali;
- γQ = 0 per i carichi accidentali;
Per i carichi sfavorevoli all’equilibrio, ovvero i carichi che determinano un aumento delle sollecitazioni, valgono invece i seguenti coefficienti parziali:
- γG1 = 1.3 per i carichi permanenti strutturali;
- γG2 = 1.5 per i carichi permanenti non strutturali (1.3 se i carichi sono compiutamente definiti nell’analisi dei carichi);
- γQ = 1.5 per i carichi accidentali.

Per ottenere le combinazioni di carico a scacchiera si utilizzerà il coefficiente parziale γG1 = 1 per i carichi permanenti strutturali che contribuiscono alla riduzione delle sollecitazioni. Ai carichi permanenti non strutturali (massetto, pavimento, intonaco etc.) e ai carichi accidentali che sono a favore dell’equilibrio saranno applicati i coefficienti parziali γG2 = 0.8 e γQ = 0. Tutti gli altri carichi saranno amplificati utilizzando i fattori parziali per condizioni sfavorevoli all’equilibrio.
Esempio di combinazioni a scacchiera
Ti mostro nelle immagini di seguito un esempio di trave continua caricata a scacchiera per la massimizzazione dei momenti in campata e agli appoggi e i diagrammi del momento che ne derivano, utilizzando i coefficienti parziali di sicurezza proposti dalla Normativa Tecnica.
Momento e taglio resistente: progetto armature, fascia piena e semipiena
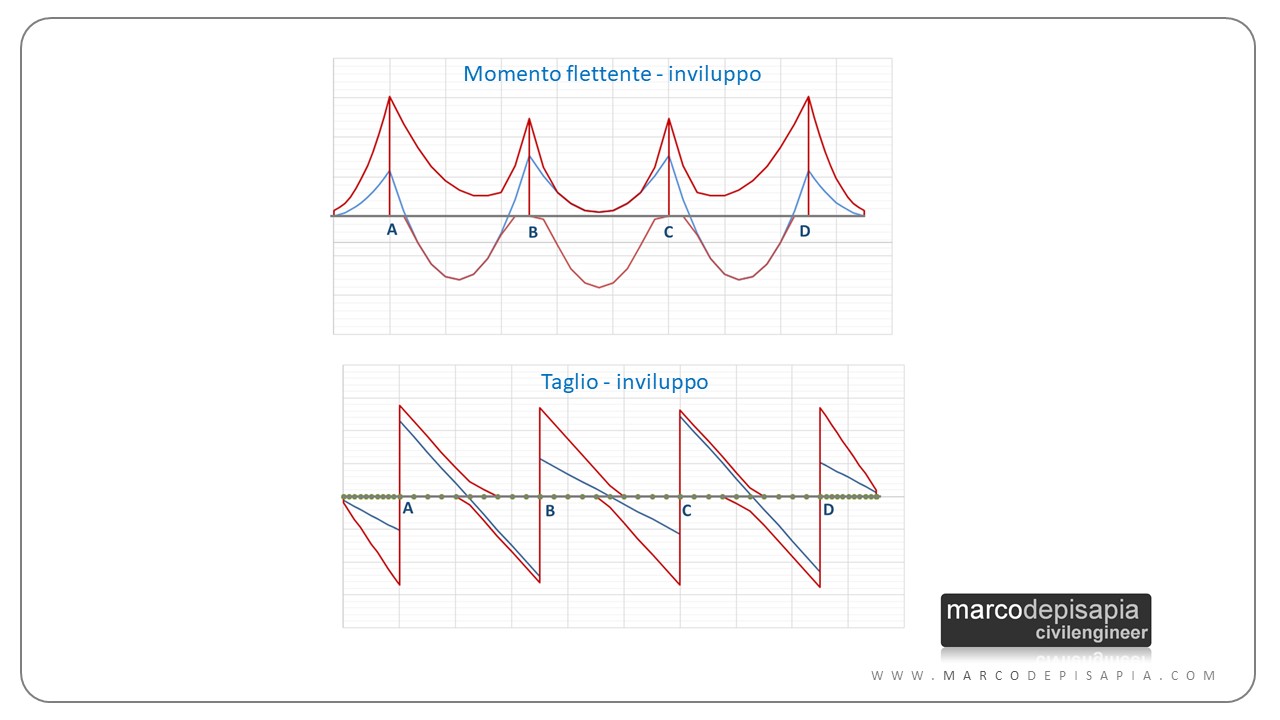
I digrammi delle sollecitazioni di momento e taglio ottenuti dalle combinazioni di carico a scacchiera vanno sovrapposti per ottenere l’inviluppo delle sollecitazioni. Una volta noto l’inviluppo delle sollecitazioni di flessione e taglio, sarà possibile progettare l’armatura longitudinale dei travetti e la fascia piena e semipiena del solaio ed eseguire le verifiche di resistenza per flessione e taglio.
Armature longitudinali: progetto e verifica
Utilizzando l’inviluppo delle sollecitazioni di momento è possibile progettare la distinta dei ferri di armatura longitudinale per i travetti del solaio. Per verificare l’armatura longitudinale dei travetti sarà sufficiente riportare nel digramma dell’inviluppo delle sollecitazioni flettenti il diagramma del momento resistente.
Fascia piena, semipiena e corrente: progetto e verifica
L’inviluppo dei diagrammi del taglio sollecitante, ci permette di progettare la lunghezza della fascia piena e semipiena del solaio in prossimità degli appoggi della trave.
Ti spiego di seguito cosa si intende per fascia piena e semipiena del solaio:
- fascia piena: vengono rimosse le pignatte fra i travetti creando di fatto una sezione rettangolare piena in calcestruzzo armato;
- fascia semipiena: vengono poste in opera le pignatte in modo alternato in modo da avere una sezione del solaio semipiena;
- fascia corrente: è la normale sezione del solaio composta da due travetti, dalle pignatte e dalla soletta.
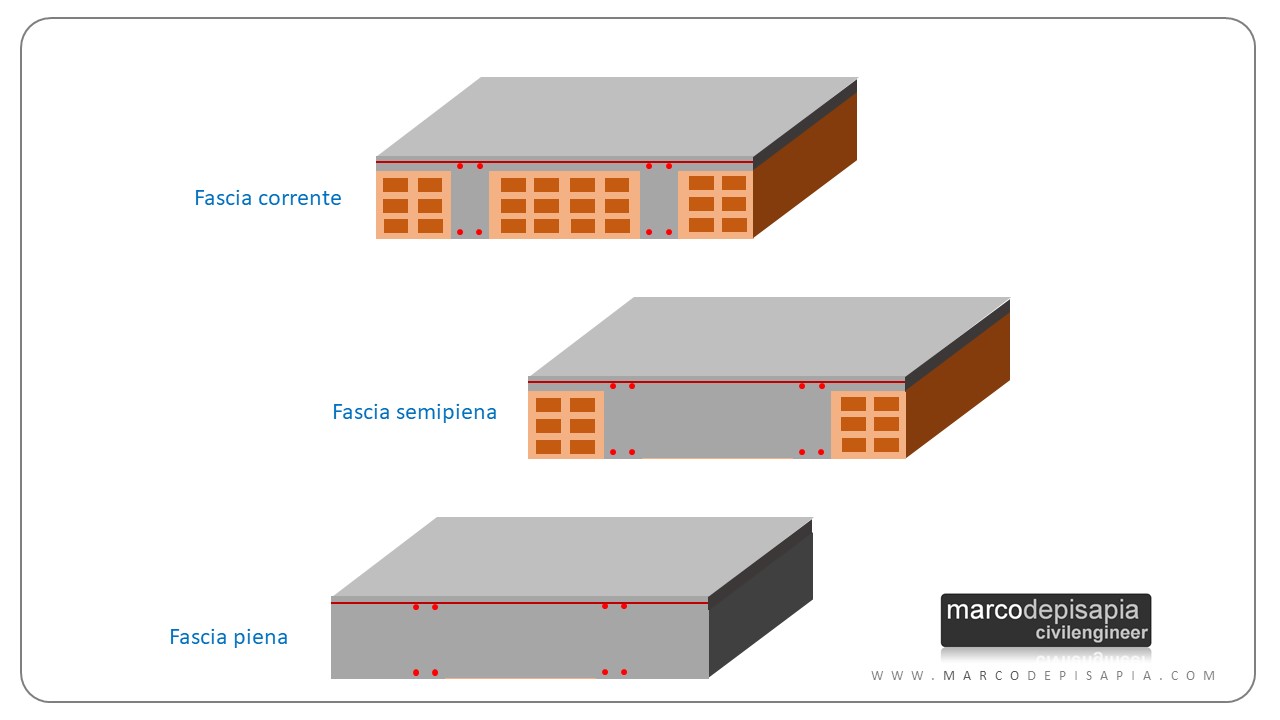
L’utilizzo della fascia piena o semipiena consente di incrementare il taglio resistente della sezione del solaio. In corrispondenza degli appoggi della trave continua si avranno i valori massimi del taglio sollecitante. In tali zone è possibile ricorrere all’utilizzo della fascia piena e semipiena per soddisfare la verifica a taglio in ogni sezione della trave.
Scarica la risorsa per il calcolo del solaio in laterocemento

Le immagini dei digrammi delle sollecitazioni di quest’articolo sono estratte dalle schermate di Ver.Sez. l’applicazione del blog per la verifica di sezioni in cemento armato. L’app Ver.Sez. è dotata di un modulo interamente dedicato al calcolo dello schema di trave continua del solaio in laterocemento, sia per nuove costruzioni che per costruzioni esistenti, con la possibilità di inserire fino a 5 campate e con tutte le combinazioni di carico a scacchiera implementate in automatico.
Nel modulo dedicato alla trave continua del solaio potrai progettare l’armatura longitudinale dei travetti, dimensionare la fascia piena e semipiena ed eseguire la verifica a flessione e taglio. Potrai stampare una dettagliata relazione tecnica contenente i tabulati delle sollecitazioni per tutte le combinazioni di carico, i diagrammi e gli inviluppi del momento e del taglio sollecitante e i diagrammi del momento e taglio resistente. Puoi scaricare la versione Premium dell’app a questo link.
Per scaricare la risorsa nella versione di prova, compila i campi qui sotto. Riceverai all’istante una email contenente il link per eseguire il download.

Conclusioni
Utilizzando nel modo corretto i coefficienti parziali di sicurezza proposti dalla Normativa Tecnica è possibile ottenere le combinazioni di carico a scacchiera per l’analisi del solaio in laterocemento. Considerare le combinazioni di carico a scacchiera ti darà la certezza che il solaio oggetto del calcolo raggiunga il massimo livello di sicurezza. Spero che la risorsa allegata all’articolo ti aiuti a velocizzare la fase di calcolo, progetto e verifica dei solai in laterocemento.
Se hai trovato utili le informazioni contenute in questo post, puoi suggerirlo ai tuoi colleghi su Linkedin o ai tuoi amici su Facebook cliccando sui tasti di condivisione social che trovi in fondo alla pagina.
Al prossimo articolo.
Marco
Aggiornato il 24/11/2019. Pubblicato il 12/12/2016.

Salve,
ho scaricato il file ma non riesco a installarlo, ho excel 2007. Come posso fare?
grazie
L’app non richiede installazione. Avvia il file eseguibile .exe con un doppio click.
Nel tuo caso devi avviare la versione specifica per Excel2007.
Ciao
Marco
Buongiorno, per chiarirmi un pò le idee stavo leggendo questo interessante articolo, ma con riferimento ai coefficienti utilizzati per la realizzazione delle “scacchiere” non mi torna qualcosa. Mi spiego meglio, i coefficienti moltiplicativi dei carichi G2k, sulle campate dove questi sono considerati come “sfavorevoli” vengo presi uguali a quelli dei carichi G1k (cosa giustamente lecita se si tratta di non strutturali compiutamente definiti) ma allo stesso tempo sulle campate adiacenti, dove il carico è considerato “favorevole”, è stato utilizzato 0,8 (che invece si riferisce al caso in cui i G2k non sono compitamente definiti) anziché 1. Spero di essere stato chiaro e di non aver preso una cantonata.
Buona giornata
VM
Ciao Vito, grazie del commento. La tua osservazione è corretta. Se per i carichi sfavorevoli G2k si utilizza gammaG = 1.3, per i carichi favorevoli G2k si dovrà utilizzare gammaG = 1, in analogia con i coefficienti parziali validi per i carichi G1k. Ciao. Marco