Diagramma momento-curvatura di sezioni in calcestruzzo armato: esempi numerici in Microsoft Excel (.xls)

In quest’articolo vedremo come calcolare il diagramma momento-curvatura di una sezione in calcestruzzo armato, da quali parametri geometrici e meccanici dipende la forma di tale diagramma e perché il legame momento-curvatura di una sezione è così importante per la progettazione strutturale in presenza dell’azione sismica.

Nel seguito dell’articolo vedremo degli esempi numerici in cui sono stati ricavati i legami momento-curvatura per sezioni in calcestruzzo armato di diverse dimensioni e con diversi quantitativi di armatura. Analizzando casi concreti, vedremo da quali parametri dipende la forma del legame momento-curvatura, la duttilità della sezione inflessa o presso-inflessa e il valore della curvatura ultima che determina il collasso della sezione.

Nel corso dell’articolo potrai scaricare gratuitamente Ver.Sez., l’app implementata in Microsoft Excel grazie alla quale potrai calcolare il diagramma momento-curvatura di una sezione in calcestruzzo armato e potrai visualizzare per ogni step di calcolo le deformazioni e le tensioni agenti nel calcestruzzo e nell’acciaio di armatura. Gli esempi numerici mostrati nel seguito dell’articolo sono stati calcolati utilizzando l’app Ver.Sez. Buona lettura!

---

Scarica l’app Ver.Sez. per il calcolo del legame momento curvatura di una sezione in calcestruzzo armato

---

Diagramma momento-curvatura: un breve richiamo sul concetto di curvatura

Prima di affrontare il tema della costruzione del diagramma momento-curvatura di una sezione in calcestruzzo armato, occorre chiarire un concetto di base: cos’è la curvatura della deformata di una trave in un suo generico punto lungo l’asse. Per capire cos’è la curvatura ti propongo un semplice esempio: il classico schema di trave appoggiata-appoggiata con un carico uniformemente distribuito. Ti riporto uno schema di seguito.

Se consideriamo la configurazione deformata della trave, in ogni punto dell’asse della trave possiamo individuare la rotazione che subisce la sezione rispetto alla configurazione indeformata in un riferimento globale. Ogni punto della configurazione deformata dell’asse della trave sarà caratterizzato da un certo valore φ della rotazione della sezione. 

Due punti sull’asse della trave, posti ad una distanza ΔX, esibiranno due diverse rotazioni (φ₁ e φ₂) della sezione. La curvatura sarà data dalla differenza fra queste due rotazioni, rapportata alla distanza ΔX che le separa. 

χ  = (φ₁ – φ₂) / ΔX = Δφ / ΔX

• χ = curvatura
• φ = rotazione della sezione
• ΔX = distanza fra le due sezioni considerate

Formula discretizzata della curvatura

Il valore della curvatura è dunque dato dal rapporto fra la differenza degli angoli di rotazione (espressi in radianti) di due sezioni della configurazione deformata e la distanza che le separa. La dimensione della curvatura sarà pari all’inverso di una distanza e si esprimerà, per esempio, in [1/mm] se le lunghezze saranno espresse in mm. Riducendo la distanza ΔX fino a farla tendere a zero, otterremo il valore della curvatura in un punto dell’asse della trave.

Per approfondire il concetto di curvatura e le formule analitiche che la descrivono puoi consultare questo post del blog in cui ho affrontato l’argomento proponendo degli esempi numerici e una risorsa interattiva implementata in Microsoft Excel.

Interpretazione geometrica della curvatura

E’ possibile dare un’interpretazione geometrica al valore della curvatura: la curvatura é pari all’inverso del raggio del cerchio osculatore della deformata nel punto considerato. Pertanto, maggiore sarà il raggio del cerchio osculatore, minore sarà la curvatura. Per raggio del cerchio osculatore tendente ad infinito, la curvatura tenderà a zero, ovvero l’asse della trave sarà rettilineo e quindi indeformato.

La curvatura può anche essere calcolata tramite l’analisi di una singola sezione in calcestruzzo armato, individuando la posizione dell’asse neutro che determina l’equilibrio fra tensioni interne e sollecitazioni esterne. Per una sezione in calcestruzzo armato inflessa il valore della curvatura sarà dato dal rapporto fra la deformazione massima nel calcestruzzo compresso e la distanza dell’asse neutro dal bordo compresso ella sezione.

---

Legame momento-curvatura: esempi numerici per sezioni in calcestruzzo armato

Ora che ti è chiaro cos’è la curvatura, possiamo analizzare il diagramma momento-curvatura di una sezione in calcestruzzo armato e individuare i 3 parametri che definiscono la sua forma, influendo sul valore della curvatura al limite elastico e della curvatura ultima.

Definita una sezione in calcestruzzo armato (dimensioni geometriche, quantità di armature e proprietà meccaniche dei materiali), a ciascun valore della curvatura corrisponderà un valore del momento resistente. Di seguito ti riporto un diagramma momento curvatura di esempio valido per una sezione rettangolare in calcestruzzo armato e calcolato con l’app Ver.Sez.

Mediante il legame momento-curvatura di una sezione in calcestruzzo armato è possibile calcolare la duttilità in termini di curvatura, individuando nel diagramma la curvatura al limite elastico (linea verticale viola nel grafico sopra) e la curvatura ultima (linea rossa tratteggiata nel grafico sopra), cui corrisponderà la rottura della sezione. 

La capacità di una struttura di dissipare energia in presenza di un evento sismico è di fondamentale importanza per la sicurezza strutturale di un edificio. A questo scopo gioca un ruolo fondamentale la duttilità degli elementi strutturali che la compongono.

Il modulo dell’app Ver.Sez. dedicato al calcolo del legame momento-curvatura ti permetterà di visualizzare, per ogni valore della curvatura, il diagramma delle deformazioni e delle tensioni di compressione nel calcestruzzo per la sezione analizzata e la profondità dell’asse neutro. Ti riporto un’immagine di esempio qui sotto.

La forma del diagramma momento-curvatura di una sezione in calcestruzzo armato è influenzato da tre parametri:

• quantità di armatura;
• entità dello sforzo normale;
• dimensioni della sezione.

Nel seguito del post vedremo in che modo ciascuno dei tre parametri elencati influisce sulla forma del diagramma momento curvatura.

Esempio numerico sul diagramma momento curvatura: variazione della quantità di armatura

Nell’esempio di seguito puoi vedere un confronto del legame momento-curvatura calcolato per tre sezioni aventi le stesse  dimensioni (30×60 cm) ma diverse quantità di armatura, pari a: 

• 4 φ16 superiori + 4 φ16 inferiori;
• 4 φ16 superiori + 6 φ16 inferiori;
• 4 φ16 superiori + 8 φ16 inferiori.

Come hai potuto vedere è stata incrementata solo l’armatura inferiore. In seguito all’incremento di armatura inferiore, il valore del momento resistente è aumentato passando da un valore minimo di circa 170 kNm (curva blu) ad un massimo di 340 kNm (curva arancione). Parallelamente però è diminuita la curvatura ultima della sezione. Il valore della curvatura ultima si è ridotto a meno della metà passando da una valore di 8.5∙10^-5 ad un valore di circa 4∙10^-5. Di conseguenza la duttilità della sezione si è più che dimezzata.

Da quest’esempio risulta evidente che disponendo una quantità di armatura eccessiva rispetto a quella strettamente necessaria per il superamento della verifica di resistenza, aumenteremo la resistenza della sezione, ma ridurremo notevolmente la sua duttilità.

---

Esempio numerico sul diagramma momento curvatura: variazione dello sforzo normale

In questo secondo esempio è stata considerata una sezione di dimensioni 40×70 armata con 4 φ16 superiori e 4 φ16 inferiori. Questa volta è stato variato lo sforzo normale agente. Sono stati analizzati i seguenti tre casi:

• sforzo normale N = 0;
• sforzo normale N = 500 kN;
• Sforzo normale N = 1000 kN.

Come puoi vedere, all’aumentare dello sforzo normale agente, aumenterà il valore del momento resistente (da 200 kNm a 450 kNm). Di pari passo però diminuirà drasticamente la curvatura ultima, passando da 8.5∙10^-5 per N=0 a 1.2∙10^-5 per N=1000 kN. Questo accade perché la distanza dell’asse neutro dal bordo compresso della sezione aumenta sempre più al crescere dello sforzo normale. Di conseguenza diminuirà la curvatura ultima in quanto essa è pari al rapporto fra la deformazione ultima nel calcestruzzo e la distanza dell’asse neutro dal bordo compresso della sezione.

Per questo motivo le sezioni delle travi (sforzo normale nullo) avranno una duttilità maggiore rispetto a quelle dei pilastri (presenza di sforzo normale) e la corretta progettazione di una struttura vuole che, in presenza di un evento sismico, le cerniere plastiche si formino nelle travi e non nei pilastri.

Esempio numerico sul diagramma momento curvatura: trave a spessore ed emergente

Nell’ultimo esempio di questo post, ti mostro la differenza fra una trave a spessore e una trave emergente, aventi la stessa identica armatura, ma dimensioni geometriche diverse:

• trave a spessore 100×20 con 4φ16 + 4φ16;
• trave emergente 30×60 con 4φ16 + 4φ16.

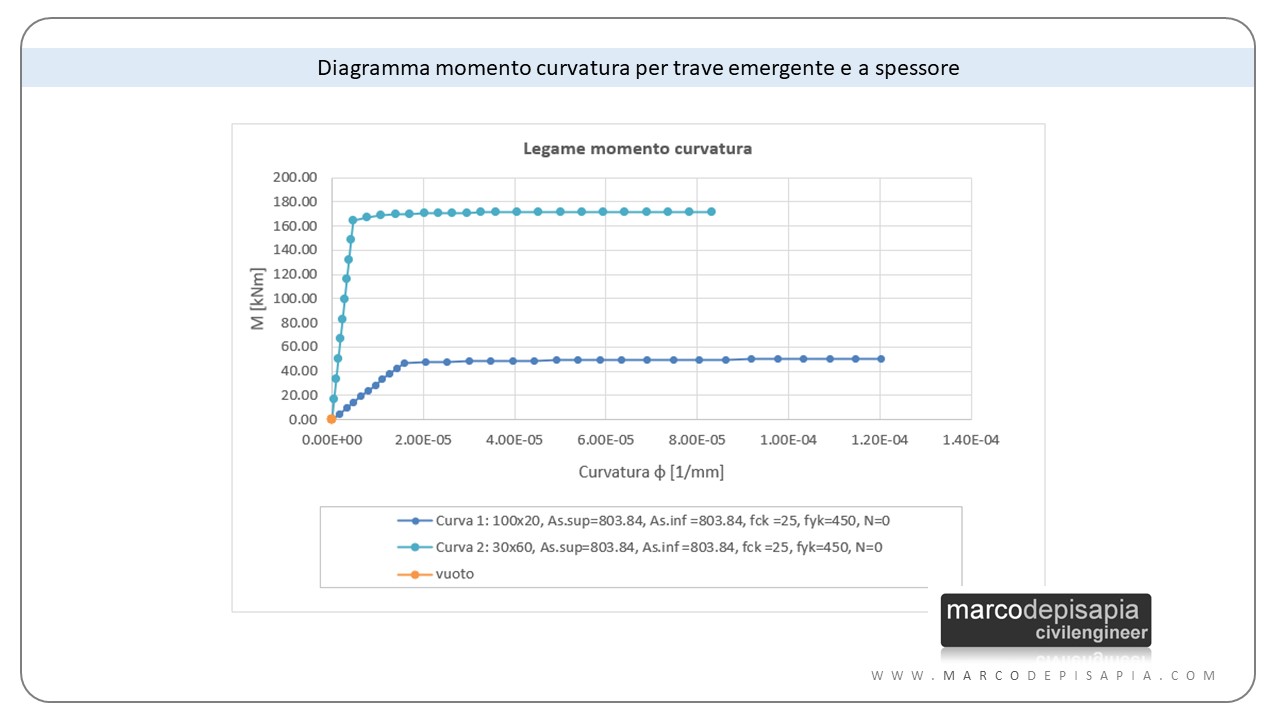
Come puoi vedere dal confronto fra le curve ottenute, passando da una trave a spessore ad una trave emergente il valore del momento resistente aumenta notevolmente (da 50 kNm a 170 kNm), mentre la curvatura ultima subisce una leggera diminuzione (da 1.2∙10^-4 a 8.3∙10^-5). Ti ricordo che, se progettiamo una struttura in Classe di Duttilità Alta, non sarà possibile inserire delle travi a spessore nei telai sismo-resistenti, ma sarà consentito solo l’uso di travi emergenti.

---

Scarica l’app Ver.Sez. per il calcolo del diagramma momento curvatura

I grafici e le immagini che ti ho mostrato in questo post sono state ottenute utilizzando l’app Ver.Sez. che condivido gratuitamente con gli iscritti al blog. Grazie a questa risorsa potrai calcolare il diagramma momento-curvatura per una qualsiasi sezione rettangolare in calcestruzzo armato, definendo le dimensioni della sezione, l’armatura e le proprietà dei materiali. Per scaricare la risorsa compila i campi qui sotto. Riceverai all’istante un’email contenente il link per eseguire il download.

---

Conclusioni

Le verifiche di resistenza allo Stato Limite Ultimo si eseguono confrontando il momento resistente in corrispondenza della curvatura ultima della sezione (punto finale del grafico momento-curvatura) con il momento sollecitante. La verifica di resistenza non tiene conto però della duttilità della sezione.

Nel caso in cui sia stata disposta un’armatura eccessiva, la verifica di resistenza sarà comunque soddisfatta, ma la duttilità della sezione non sarà adeguata all’entità di energia da dissipare in caso di sisma. Ecco perché la Normativa Tecnica prescrive di rispettare dei limiti sulle quantità di armatura da disporre in funzione della classe di duttilità con cui scegliamo di progettare la struttura (classe di duttilità Alta o Bassa) e, in determinati casi, l’esecuzione della verifica sulla duttilità di curvatura.

Il post di oggi finisce qui. Spero ti sia stato utile per approfondire questi importanti aspetti della progettazione strutturale. Se l’hai trovato utile puoi suggerirlo ai  tuoi amici su Facebook o ai tuoi colleghi su LinkedIn cliccando sui tasti di condivisione che trovi in fondo alla pagina.

Al prossimo post.

Marco

---

Ultimo aggiornamento in data 22/5/2024. Pubblicato il 29/1/2018. Codice articolo: 220.

---