Quando progettiamo una nuova costruzione in zona sismica nella maggior parte dei casi eseguiremo un’analisi modale con spettro di risposta. Lo spettro di risposta ci dice quale sarà l‘accelerazione massima a cui sarà sottoposta la struttura durante un evento sismico con una data probabilità di accadimento. In quest’articolo ti spiego come sono stati ottenuti gli spettri di risposta elastici che utilizziamo ogni qual volta eseguiamo la progettazione e verifica di una costruzione in zona sismica.

Alla fine dell’articolo potrai scaricare gratuitamente una risorsa interattiva che ti permetterà di calcolare la risposta di un oscillatore semplice sottoposto alle accelerazioni di un accelerogramma storico registrato durante un evento sismico.
Scarica EarthQuake: la guida pratica per l’analisi sismica delle strutture

EarthQuake è la guida in formato cartaceo e digitale sull’analisi sismica delle strutture, organizzata in aree tematiche secondo un percorso chiaro e preciso. Grazie alla guida EarthQuake potrai approfondire le tematiche dell’analisi sismica delle costruzioni con un approccio pratico e dal taglio divulgativo.
Compila i campi qui sotto per scaricare l’estratto gratuito. Riceverai all’istante una mail contenente il link per eseguire il download.

Cosa sono gli spettri di risposta (e come si calcolano)
Lo spettro di risposta elastico in termini di accelerazione è un grafico che riporta, in funzione del periodo naturale di vibrazione di una costruzione ipotizzata a comportamento indefinitamente elastico, l’accelerazione massima che subirà quando sarà investita da un evento sismico con una data probabilità di accadimento.
Lo spettro di risposta è uno strumento molto potente per la progettazione strutturale in zona sismica. Conoscendo solo il periodo di vibrazione della costruzione e le masse degli impalcati, ci permetterà di valutare l’azione sismica massima che la struttura dovrà essere in grado di sopportare.
Spettri di risposta elastici: i parametri in gioco
La forma dello spettro di risposta e i valori delle accelerazioni sismiche dipendono dai seguenti parametri:
- la pericolosità del sito, calcolata in funzione delle sue coordinate geografiche (latitudine e longitudine). Tutti i dati sulla pericolosità sismica del sito sono contenuti negli allegati A e B delle vecchie NTC2008, riferiti ad un reticolo composto da ben 10751 punti che ricopre tutto il territorio nazionale;
- la categoria di sottosuolo (la Normativa Tecnica ne prevede 5 denominate: A, B, C, D ed E);
- le condizioni topografiche (superficie pianeggiante o presenza di rilievi);
- la probabilità di accadimento dell’evento sismico in funzione dello stato limite considerato (per Stato Limite di Salvaguardia della Vita il periodo di ritorno vale 475 anni );
- la vita nominale dell’opera;
- la classe d’uso dell’opera (opere con normali affollamenti, opere con funzioni pubbliche strategiche etc.)
- il valore dello smorzamento della costruzione (in genere si assume convenzionalmente uno smorzamento pari al 5% per le costruzioni).
Una volta noti tutti i parametri elencati sopra è possibile utilizzare le formule proposte dalla Normativa Tecnica per calcolare lo spettro di riposta elastico. Ti riporto qui sotto, a scopo di esempio, un’immagine che raffigura gli spettri di risposta elastici conformi alle prescrizioni delle NTC2018 e corrispondenti ad un dato sito geografico, per le diverse categorie di sottosuolo.
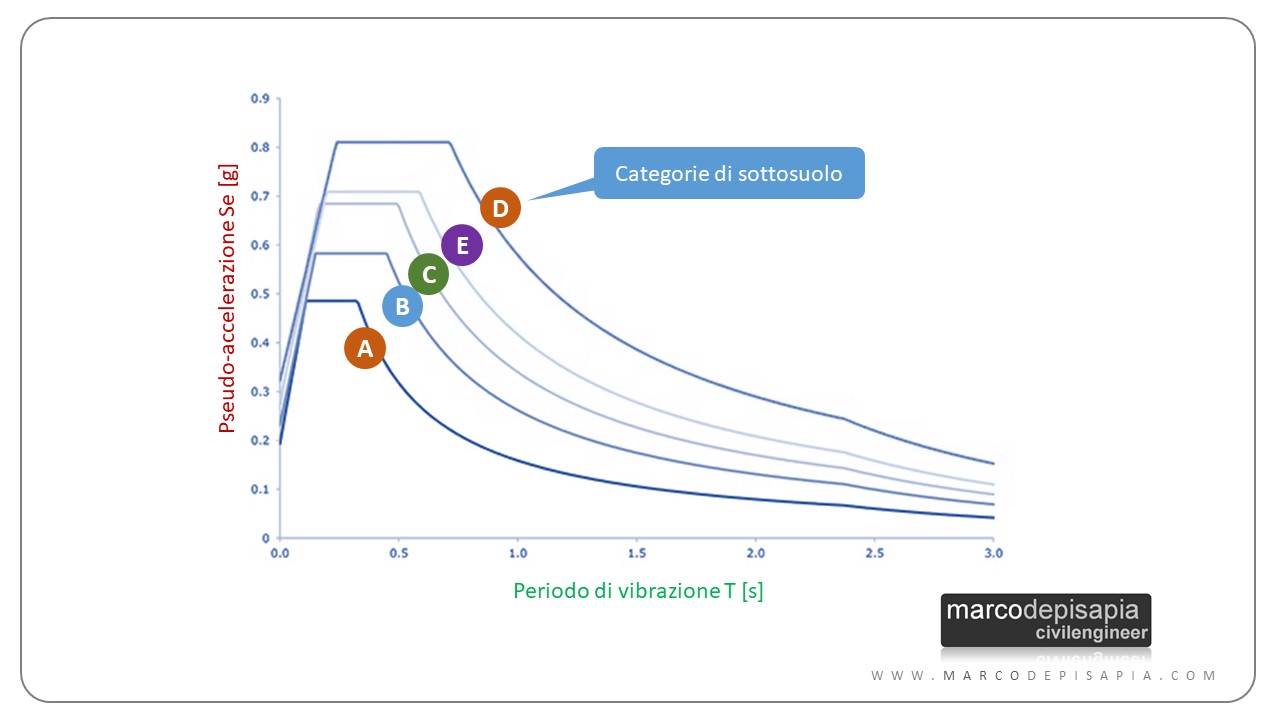
L’entità dell’azione sismica che solleciterà una costruzione, oltre a dipendere da tutti i parametri elencati sopra, dipenderà da un’altro importantissimo fattore: il periodo naturale di vibrazione della costruzione. Il valore del periodo di vibrazione a sua volta dipende da com’è stata concepita la struttura: dalle sezioni e lunghezze dei pilastri, delle travi e dei setti, dalla loro disposizione in pianta, dalla massa degli impalcati. In sintesi il periodo naturale di vibrazione di una costruzione dipende dalla rigidezza traslante della struttura e dalla massa dell’edificio.
Ora che sai come ottenere gli spettri di risposta applicando le prescrizioni della Normativa Tecnica, veniamo al punto chiave di questo post: come sono state ottenute le forme spettrali che la Normativa propone di utilizzare per la valutazione dell’azione sismica agente su una struttura? Continua a leggere per scoprirlo.
Spettri di risposta elastici: tutto inizia da un lollipop
Il procedimento che ha portato alla valutazione degli spettri di risposta elastici parte da un sistema fisico molto semplice: un oscillatore ad un solo grado di libertà, meglio noto come oscillatore semplice. Quest’oggetto può essere schematizzato in diversi modi:
- una massa che scorre su un piano orizzontale senza attrito, collegata ad una molla;
- un telaio piano ad una campata e ad un livello con traverso rigido;
- una colonna di rigidezza k con una massa concentrata alla sommità.
L’ultima schematizzazione dell’elenco è molto frequente nell’analisi dinamica delle strutture. La sua forma ricorda molto quella di un lollipop (ovvero un lecca-lecca) e di fatto alcuni testi scientifici, per esempio il testo di Alan Williams, definiscono questo modello come lollipop structure, ovvero struttura a lollipop.
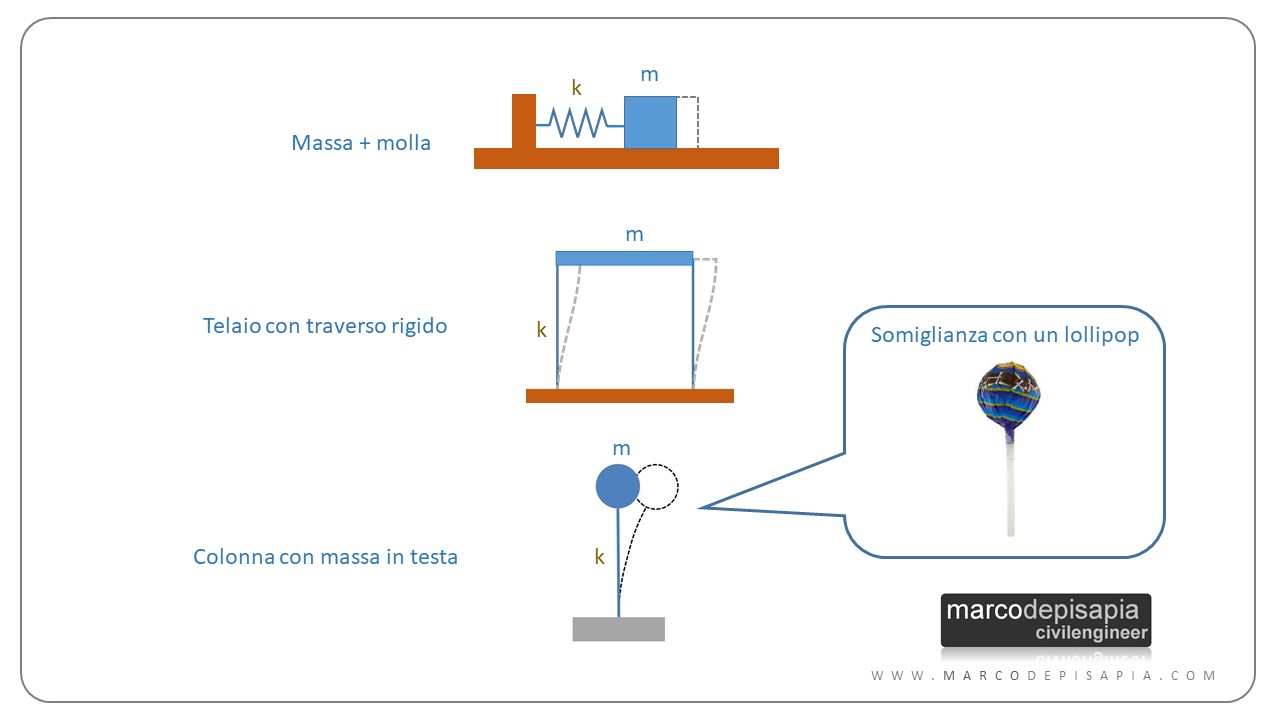
Le caratteristiche di un oscillatore semplice sono tre:
- la massa concentrata alla sommità;
- la rigidezza traslante dell’asta che dipende dalla sua lunghezza e dalla sua sezione;
- lo smorzamento viscoso che determina la progressiva riduzione dell’ampiezza delle oscillazioni nel tempo a causa delle proprietà viscose dei materiali.
Il periodo naturale di vibrazione dell’oscillatore semplice è una caratteristica che dipende dalla massa e rigidezza del sistema e può essere calcolato mediante la seguente formula:
T = 2 ⋅ π √ (m / k)
- m = massa del sistema;
- k = rigidezza del sistema.
Formula del periodo naturale di vibrazione di un oscillatore semplice
Per una struttura a lollipop è molto semplice far variare il periodo di vibrazione: basterà variare l’entità della massa concentrata alla sommità oppure la lunghezza della colonna. All’aumentare della massa aumenterà il periodo di vibrazione, a parità di rigidezza. A parità di massa, all’aumentare della lunghezza della colonna diminuirà la rigidezza del sistema e di conseguenza aumenterà il suo periodo di vibrazione. Per far variare il periodo di vibrazione di un oscillatore semplice schematizzato come un lollipop possiamo scegliere di intervenire solo sulla massa, solo sulla lunghezza della colonna, oppure su entrambi i parametri.
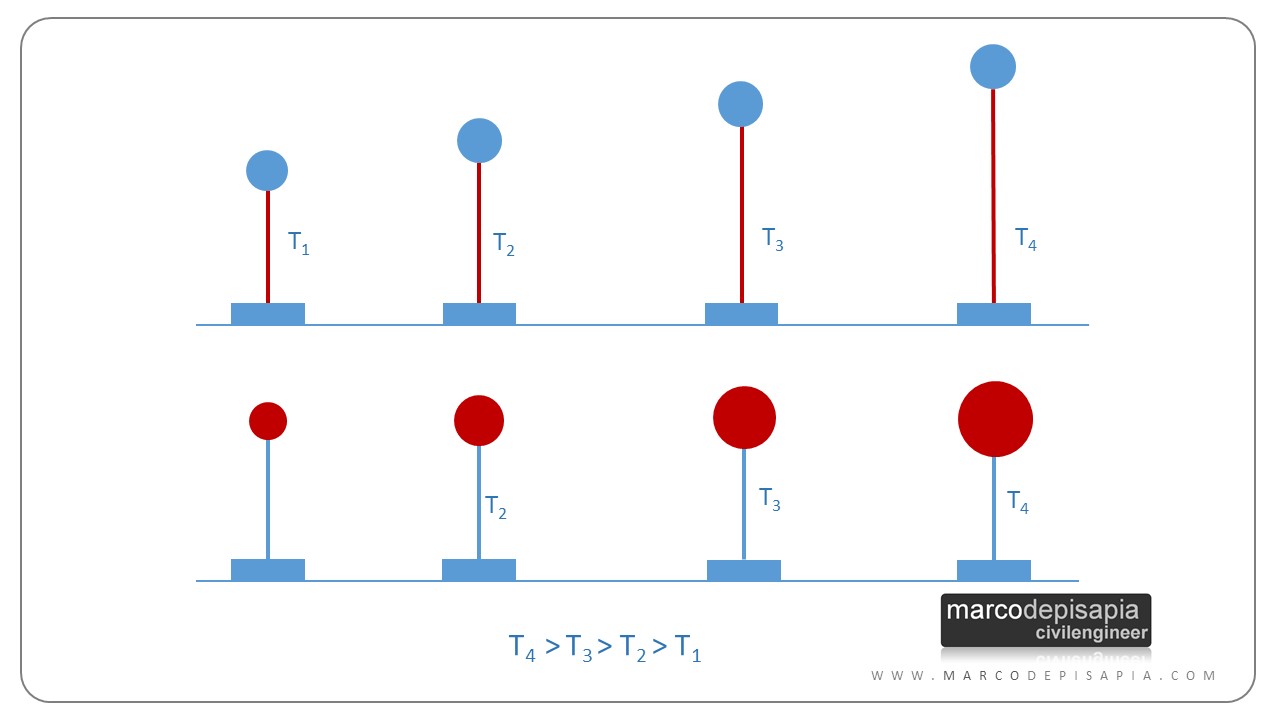
I 4 step per il calcolo degli spettri di risposta elastici
Nel seguito del post ti illustro i 4 step del procedimento necessario per ottenere gli spettri di risposta elastici che tutti i progettisti di strutture utilizzano per le analisi in combinazione sismica.
1. Selezione degli accelerogrammi da fornire in input
Per ottenere uno spettro di risposta il primo passo da compiere è reperire gli accelerogrammi storici di eventi sismici caratterizzati dalla stessa probabilità di accadimento. Un accelerogramma è la registrazione istante per istante dell’accelerazione che manifesta il suolo durante un evento sismico. Queste registrazioni vengono effettuate da apposite stazioni sismiche.
In Italia le registrazioni degli eventi sismici venivano in origine effettuate dalla rete Enea-Enel, creata nel 1973, i cui sismografi erano collocati nelle cabine di trasformazione elettrica Enel. Oggi tale rete è stata ampliata fino ad arrivare a 580 postazioni permanenti e temporanee distribuite su tutto il territorio nazionale, dando vita alla RAN (rete accelerometrica nazionale).
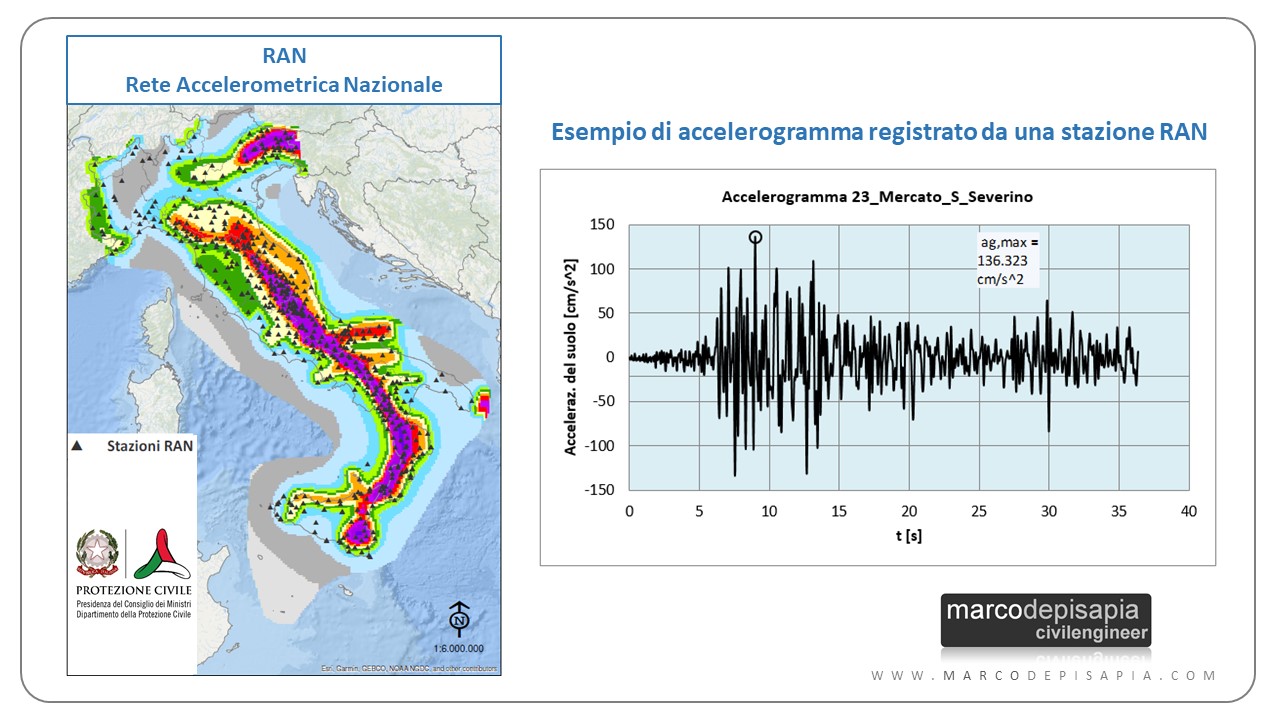
2. Valutazione della risposta dell’oscillatore semplice
Le accelerazioni degli accelerogrammi storici selezionati vengono applicate alla base della struttura a lollipop per studiare la risposta del sistema in termini di spostamento relativo, accelerazione e velocità. Per “risposta” si intende la conoscenza istante per istante delle grandezze citate sopra.
Per ottenere la risposta dell’oscillatore bisogna risolvere le equazioni differenziali del moto dell’oscillatore semplice mediante un’analisi al passo, utilizzando un metodo di integrazione numerica come per esempio il metodo di Newmark. La risposta massima in termini di accelerazione verrà riportata nel grafico dello spettro di risposta in corrispondenza del periodo naturale di vibrazione dell’oscillatore analizzato.

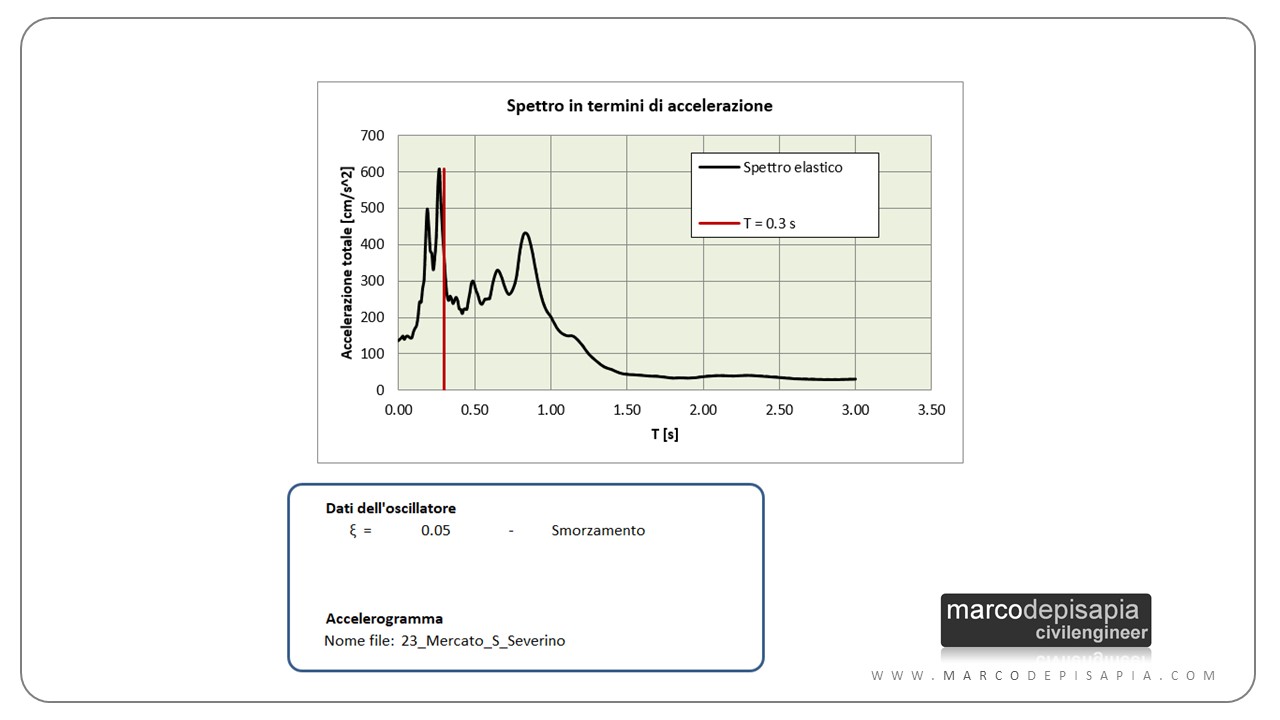
Nell’immagine sopra puoi vedere la risposta di un oscillatore con periodo di vibrazione T = 0.3 s e smorzamento ξ pari a 0.05 ad un accelerogramma storico. La risposta è stata ottenuta utilizzando la risorsa utility interattiva che potrai scaricare tra poco.
3. Valutazione dello spettro di risposta in termini di accelerazione
Ai fini del progetto e verifica di una struttura in zona sismica non è necessario conoscere la risposta istante per istante ad un evento sismico. Quello che interessa ad un progettista è la risposta massima che manifesta la struttura, in particolare l’accelerazione massima. Per questo motivo si ricorre alla costruzione degli spettri di risposta.
Lo step 2 viene ripetuto per valori crescenti del periodo di vibrazione dell’oscillatore semplice per ricoprire il range di periodi di vibrazione delle costruzioni: da zero a quattro secondi circa. Riportando le accelerazioni massime ottenute in funzione dei periodi di vibrazione degli oscillatori analizzati si costruirà lo spettro di risposta corrispondente all’accelerogramma utilizzato in input.
Nell’immagine sotto puoi vedere lo spettro di risposta relativo ad un solo accelerogramma. Per ottenerlo sono stati analizzati 52 oscillatori semplici con periodo crescente da 0.02 secondi a 3 secondi.
4. Iterazione del procedimento e inviluppo degli spettri
Utilizzare lo spettro di risposta all’accelerogramma di un singolo evento sismico non consente di raggiungere un livello di sicurezza adeguato. Lo step 3 viene ripetuto per un adeguato numero di accelerogrammi di eventi sismici caratterizzati da una prefissata probabilità di accadimento. Sovrapponendo gli spettri di risposta ottenuti si ricava l’inviluppo delle accelerazioni massime che gli oscillatori semplici analizzati subiscono in risposta a tutti gli accelerogrammi selezionati. Puoi vedere nell’immagine qui sotto cosa si ottiene sovrapponendo gli spettri in termini di accelerazione, ciascuno corrispondente ad un diverso accelerogramma.
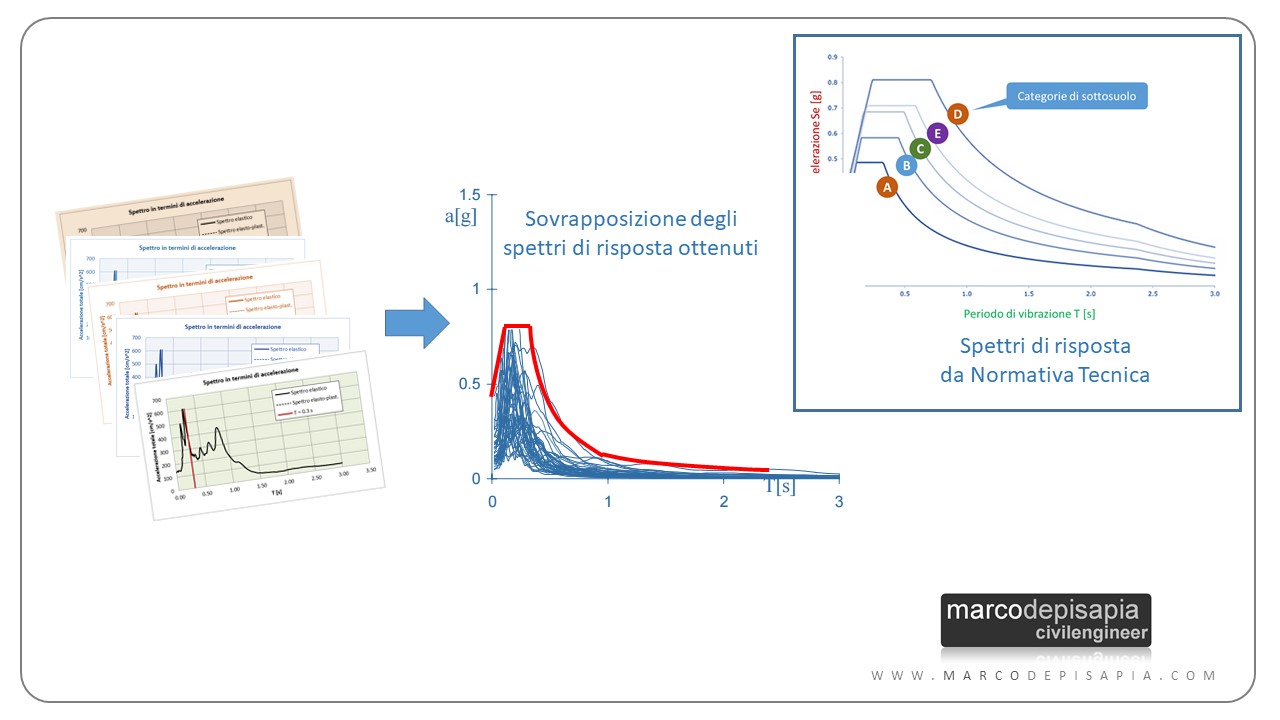
Ti ricorda qualcosa la forma dell’inviluppo degli spettri di risposta? Prova a confrontarlo con la forma degli spettri di risposta elastici forniti dalla Normativa Tecnica. Gli spettri di risposta proposti dalla Normativa Tecnica non sono altro che l’inviluppo degli spettri di risposta in termini di accelerazione di una famiglia di oscillatori semplici con periodo di vibrazione crescente sottoposti ad accelerogrammi di eventi sismici rappresentativi.
Spettri di risposta elastici: il procedimento in sintesi
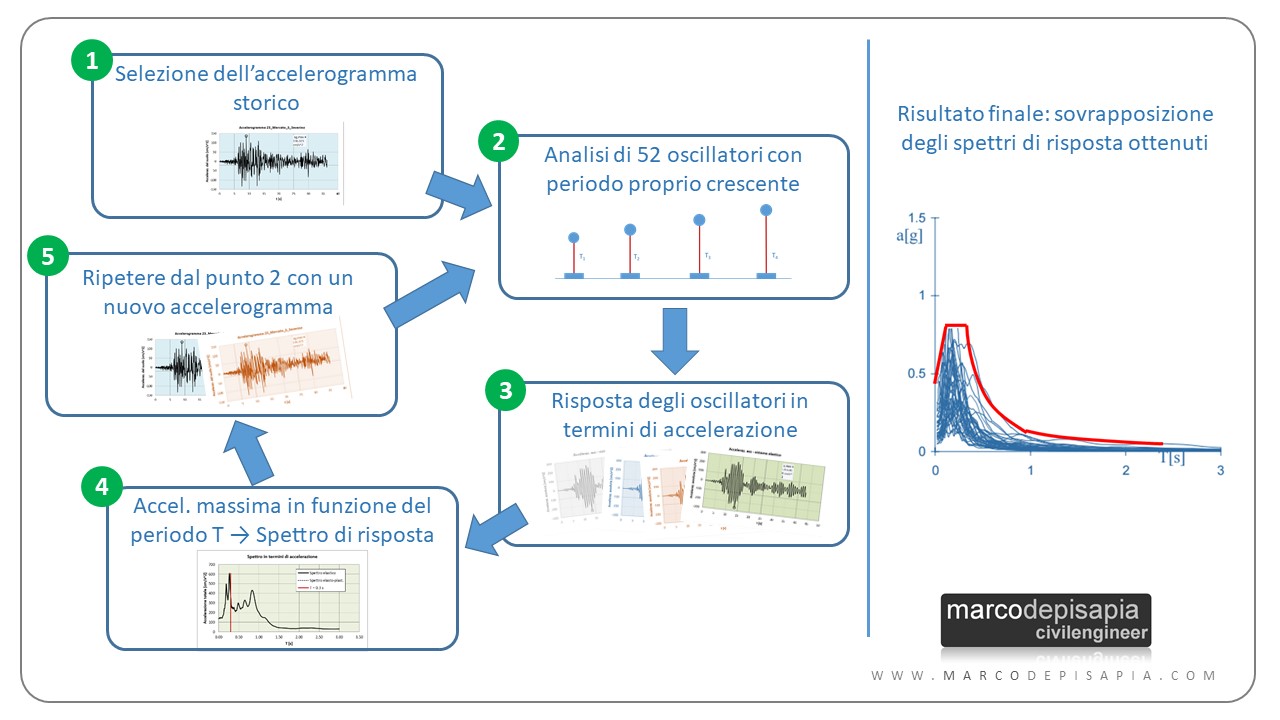
Nell’immagine qui sotto ti riporto in sintesi il procedimento utilizzato per ottenere gli spettri di risposta.
Scarica la risorsa per il calcolo della risposta di un oscillatore semplice
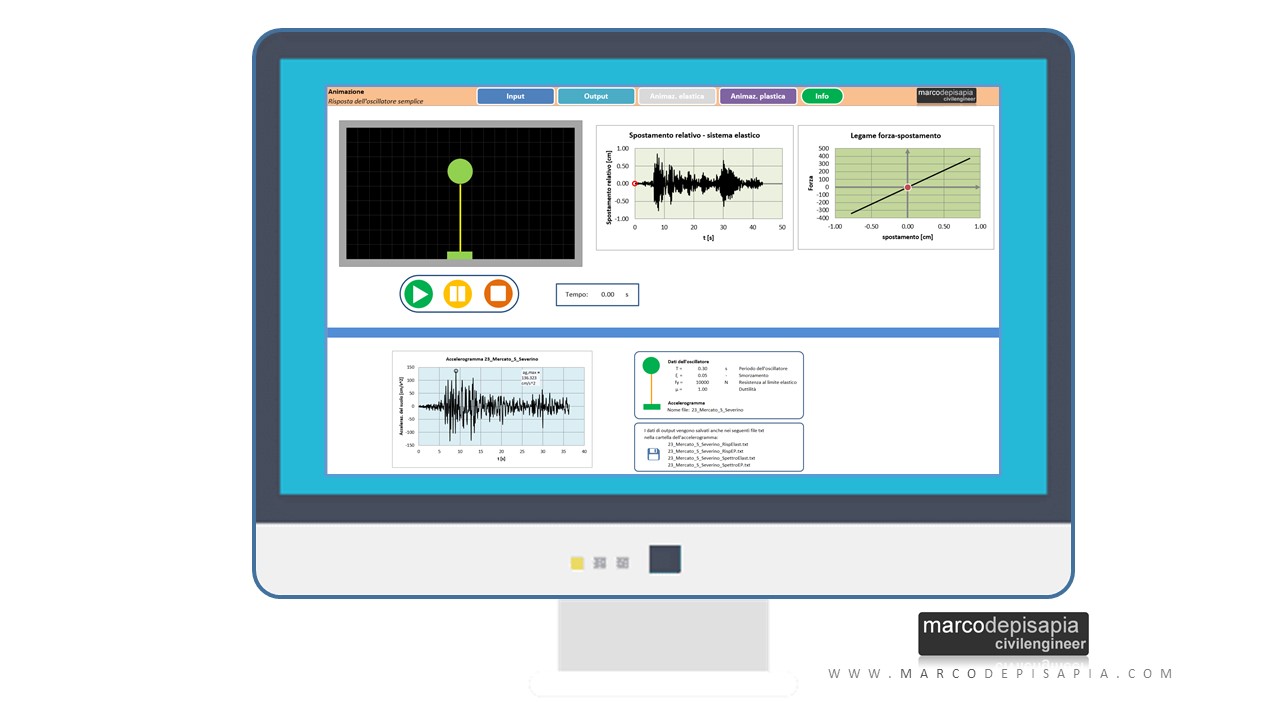
Le immagini di quest’articolo sono state ottenute utilizzando la risorsa utility che puoi scaricare di seguito. Potrai valutare la risposta di un oscillatore semplice ad un accelerogramma storico di input. Potrai ottenere la risposta in termini di spostamento relativo, accelerazione e velocità, sia per comportamento elastico che elasto-plastico. In allegato alla risorsa troverai una selezione di 30 accelerogrammi storici da utilizzare come input. Per scaricare la risorsa compila i campi qui sotto, riceverai all’istante una mail contenente il link per eseguire il download.

Nota: l’algoritmo di risoluzione che implementa l’analisi al passo con il metodo di Newmark contenuto nella risorsa utility è stato sviluppato dal Prof. Aurelio Ghersi dell’Università di Catania. L’algoritmo è reperibile in un cd-rom allegato al libro di testo Edifici anitisismici in cemento armato (libro che ti consiglio vivamente di leggere se ti interessa la progettazione di edifici in zona sismica).
Guarda il video sugli spettri di risposta elastici
Conclusioni
Gli spettri di risposta sono un potente strumento in grado di fornire l’accelerazione massima che un edificio può subire in funzione del suo periodo di vibrazione, del sito geografico e del tipo di sottosuolo.
Come hai potuto vedere, dietro il semplice grafico di uno spettro di risposta c’è un bel po’ di lavoro. Se non esistessero gli spettri di risposta, per ottenere la risposta massima di una costruzione in zona sismica bisognerebbe reperire gli accelerogrammi di eventi sismici rappresentativi della zona di interesse e analizzare la struttura con un’analisi dinamica al passo, lineare o non lineare, con un notevole onere computazionale. Per fortuna c’è chi ha già fatto questo lavoro per noi, analizzando un oggetto molto semplice: un lollipop.
Se sei arrivato fin qui la progettazione in zona sismica è sicuramente un argomento di interesse per la tua professione o per il tuo percorso di studi. Conoscevi già il procedimento usato per ottenere gli spettri di risposta? Puoi farmelo sapere lasciando un commento in fondo alla pagina. Se l’articolo ti è piaciuto che ne dici di suggerirlo ai tuoi colleghi su Linkedin o ai tuoi amici su Facebook cliccando sui tasti di condivisione social qui sotto? Te ne sarei grato :).
Ci leggiamo al prossimo articolo.
Marco
Risorsa consigliata
Libro di testo: Edifici anitisismici in cemento armato di Aurelio Ghersi.
Aggiornato il 17/11/2019. Pubblicato il 23/5/2016


Ciao, sono una studentessa di ingegneria. Sto studiando dinamica delle strutture e nella parte relativa agli spettri di risposta ho un pò di dubbi che spero con il tempo di riuscire a sciogliere. Leggendo il tuo articolo mi sembra tutto chiaro, ma studiando il mio prof parla non tanto di “sovrapposizione” degli spettri di risposta. Anzi quello che capisco è che lo spettro di risposta in accelerazione è il luogo dei punti che ad ogni periodo associa il massimo in valore assoluto dell’accelerazione massima assoluta. (scusa il gioco di parole),
nella pratica però è conveniente risalire semplicemente alla PSA(T), che serve perchè con essa (e al variare di essa), posso sfruttare il calcolo probabilistico di pericolosità sismica per ottenere la curva di pericolosità la quale mette in relazione una misura di intensità (PSA) e il tasso medio annuo di terremoti che superano una certa soglia (l’ INGV ha costruito queste curve per ogni sito in italia per diversi periodi da 0 a 2s). Da questa curva, entrando con un certo tasso e/o periodo di ritorno ottengo, al variare del periodo strutturale, tante pseudoaccelerazioni che vanno poi a definire lo spettro di pericolosità uniforme. Ora per evitare tutto il casino, sfruttiamo i dati INGV fissando Tr, otteniamo ag ( e altri 2 parametri) tali da poter definire autonomamente questo spettro che altrimenti andrebbe valutato considerando tutte le curve di pericolosità del sito (quindi si tratta di ripetere tutta l’analisi di pericolosità sismica ). la forma dello spettro da normativa sarebbe equiparabile allo spettro a pericolosità uniforme . O non ho capito niente?
Ciao Marlena, ti suggerisco una serie di articoli che possono aiutarti a chiarire le idee:
https://www.marcodepisapia.com/spettri-elastici-il-laborioso-processo-che-li-ha-generati-video/
https://www.marcodepisapia.com/analisi-modale-con-spettro-di-risposta-resa-facile-e-interessante-video/
https://www.marcodepisapia.com/azione-sismica-ntc2018-excel/
Articolo semplice e chiaro, come sempre del resto. Solo una domanda: per le strutture che non possono essere schematizzare come lollipop (oscillatori ad un grado di libertà), lo spettro si utilizza dopo la determinazione dei modi di vibrare (cioè dopo l’analisi modale)?
Ciao Giuseppe, lo spettro di risposta si utilizza per eseguire l’Analisi modale con Spettro di risposta, quindi dopo aver determinato i modi di vibrare della struttura. Trovi una spiegazione in questo video: https://www.marcodepisapia.com/analisi-modale-con-spettro-di-risposta-resa-facile-e-interessante-video/
Bravo, dopo Nakamura (30 anni fa), sei il primo in Italia che sa esprimersi con competenza su un argomento da molti ignorato o non compreso. Se non obbligatorie delle analisi geologiche, tanti, ne farebbero a meno. Molti, li usano per fare volume cartaceo. Nelle Università c’è chi insegna ancora che le strutture si “devono lesionare”. Continua così bravo, l’ingegneria edile da noi ne ha di bisogno. Non si lesionano i microscopici circuiti elettronici e le strutture di apparati militari ed aerospaziali a dimostrazione di come si possano realizzare manufatti capaci di resistere, ed ottimamente, ad eccezionali stress sia termici che dinamici per cui vergognoso rimane l’effetto rovinoso, specie in vite umane, di terremoti altrove iniqui. Un ottavo grado in Patagonia, trema; da noi, un sesto e la strage è assicurata.
Grazie del commento 😉