Quando esegui un calcolo strutturale con il tuo software di calcolo sei sicuro che venga tenuto correttamente in conto il momento torcente sollecitante? C’è un caso in cui il tuo software potrebbe commettere un errore, trascurandolo.

Ciò accade in particolare nell’analisi di strutture in acciaio realizzate con profili sottili aventi sezioni non doppiamente simmetriche (ovvero sezioni che hanno un solo asse di simmetria oppure nessuno, per esempio sezioni ad L o a C). In tal caso il tuo software di calcolo potrebbe commettere un errore trascurando un elemento importante per questo tipo di sezione: la posizione del centro di taglio.
Ma andiamo con ordine. Nel post di oggi ti spiego cos’è il centro di taglio, gli effetti che produce in termini di sollecitazioni e come tenerne conto nel modo corretto nel tuo software di calcolo strutturale. Fra pochi minuti ti sarà tutto più chiaro.
Che cos’è il Centro di Taglio
Se segui da un po’ di tempo questo blog saprai che mi piace dare un taglio molto pratico agli argomenti che affronto nei diversi post. Pertanto non mi sognerei mai di riportarti le equazioni differenziali alle derivate parziali e gli integrali del lavoro mutuo tra tensioni e deformazioni che entrano in gioco per calcolare il centro di taglio di una sezione.
Voglio mostrarti invece cos’è il centro di taglio di una sezione usando solo tre immagini. Scommettiamo che saranno sufficienti per chiarirti una volta per tutte cos’è il centro di taglio e perchè è così importante? Continua a leggere.
Le immagini riguardano un esperimento pratico, molto semplice da riprodurre volendo. Sono necessari un profilo con sezione a C in PVC (lo trovi in qualsiasi negozio di bricolage), una vite filettata, due bulloni ed un pezzo di fil di ferro (puoi usare anche dello spago).
Nell’esperimento che ti propongo, il modellino creato riproduce lo schema di una trave a mensola con un carico concentrato all’estremità. Facendo scorrere il bullone lungo la vite, avvitandolo o svitandolo, è possibile applicare il carico in diverse posizioni lungo l’asse di simmetria orizzontale della sezione.
Partiamo subito con la prima immagine:

Come puoi vedere dall’immagine sopra, la forza applicata all’estremità del profilo genera un abbassamento, ma anche una rotazione della sezione. Ciò accade perchè la forza non è applicata nel Centro di Taglio.
Possiamo intuitivamente già farci un’idea di cosa sia il centro di taglio. Il centro di taglio è quel particolare punto della sezione in cui se applico una forza concentrata, avrò solo sollecitazioni di taglio e flessione, ma nessuna sollecitazione di torsione e di conseguenza nessuna rotazione della sezione.
Puoi ben vedere quindi che il punto di applicazione della forza visto nella prima immagine non è il centro di taglio della sezione. Proviamo a fare un altro tentativo. Passiamo alla seconda immagine. Stavolta non c’è bisogno della vite filettata per applicare il carico. Il filo di ferro è stato collegato tramite un foro praticato nell’ala inferiore del profilo.

Cosa succede? Anche stavolta si ha una rotazione della sezione oltre che un abbassamento dell’asta. Stavolta però la rotazione avviene nel verso opposto. Neanche questo punto di applicazione del carico rappresenta il centro di taglio della sezione. Ma se il punto di applicazione della prima immagine mi dà una rotazione antioraria della sezione e il secondo mi dà una rotazione oraria, vuoi vedere che forse il centro di taglio è in un punto compreso fra gli ultimi due?
Passiamo allora al terzo tentativo e quindi alla terza immagine. Eccola qui sotto.

Trovato. Per il punto di applicazione del carico mostrato nella terza immagine, si avrà solo un abbassamento dell’asta, di conseguenza nessuna rotazione della sezione e nessuna sollecitazione di torsione. Possiamo quindi dedurre che per un profilo a C, il centro di taglio si trova all’esterno della sezione, sull’asse di simmetria orizzontale, spostato leggermente a sinistra rispetto all’anima verticale.
Regole utili per determinare il centro di taglio

Come ti ho già detto non ho intenzione di riportarti tutte le equazioni alla base del calcolo del centro di taglio. Per quelle ti basta aprire un qualsiasi testo di Scienza delle Costruzioni (buona fortuna :D).
Penso sia più utile e pratico riportare due semplice regole che ti permetteranno di individuare qualitativamente dove si trova il centro di taglio di una sezione:
- Il centro di taglio si trova sempre su un asse di simmetria della sezione; se una sezione ha due assi di simmetria allora il centro di taglio sarà già noto e si troverà all’intersezione dei due assi e quindi nel baricentro della sezione;
- per una sezione con un solo asse di simmetria, il centro di taglio si troverà sull’asse di simmetria della sezione;
Se la sezione non avrà assi di simmetria, allora dovrai calcolare la posizione del centro di taglio, magari utilizzando un’applicazione per l’analisi delle sezioni.
Gli effetti del Centro di Taglio nel tuo modello di calcolo
Quando ti trovi a modellare una struttura composta da profili sottili con sezioni che non sono doppiamente simmetriche, allora dovrai porre attenzione alla posizione effettiva del centro di taglio.
Generalmente i software di calcolo modellano le aste strutturali come elementi monodimensionali rappresentati dall’asse baricentrico della sezione. L’eccentricità fra baricentro della sezione e centro di taglio fa sì che ci siano anche delle sollecitazioni di torsione sul profilo caricato. Ma se l’asta è rappresentata dall’asse baricentrico, nei risultati di calcolo del tuo modello non ci sarà traccia del momento torsionale che ne deriva. In tal caso dovrai assegnare manualmente un momento torcente pari al prodotto fra l‘intensità del carico distribuito e l’eccentricità fra baricentro e centro di taglio.
Ti mostro l’esempio di un telaio semplice avente una trave con sezione a C del tipo UPN100. Il carico distribuito applicato nel baricentro geometrico della trave, genererà anche un momento torcente sollecitante. Ti riporto sotto lo schema del telaio e i profili utilizzati.
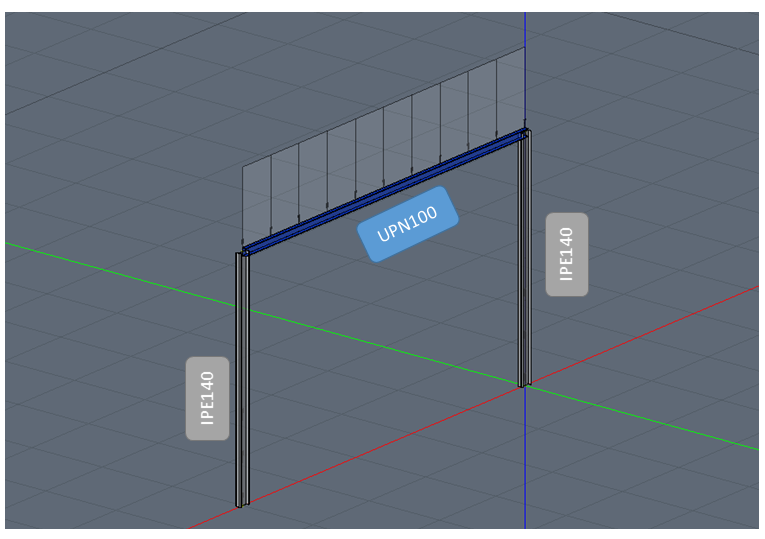
Ecco di seguito la deformazione torsionale e l’abbassamento della trave per effetto dell’eccentricità del centro di taglio:
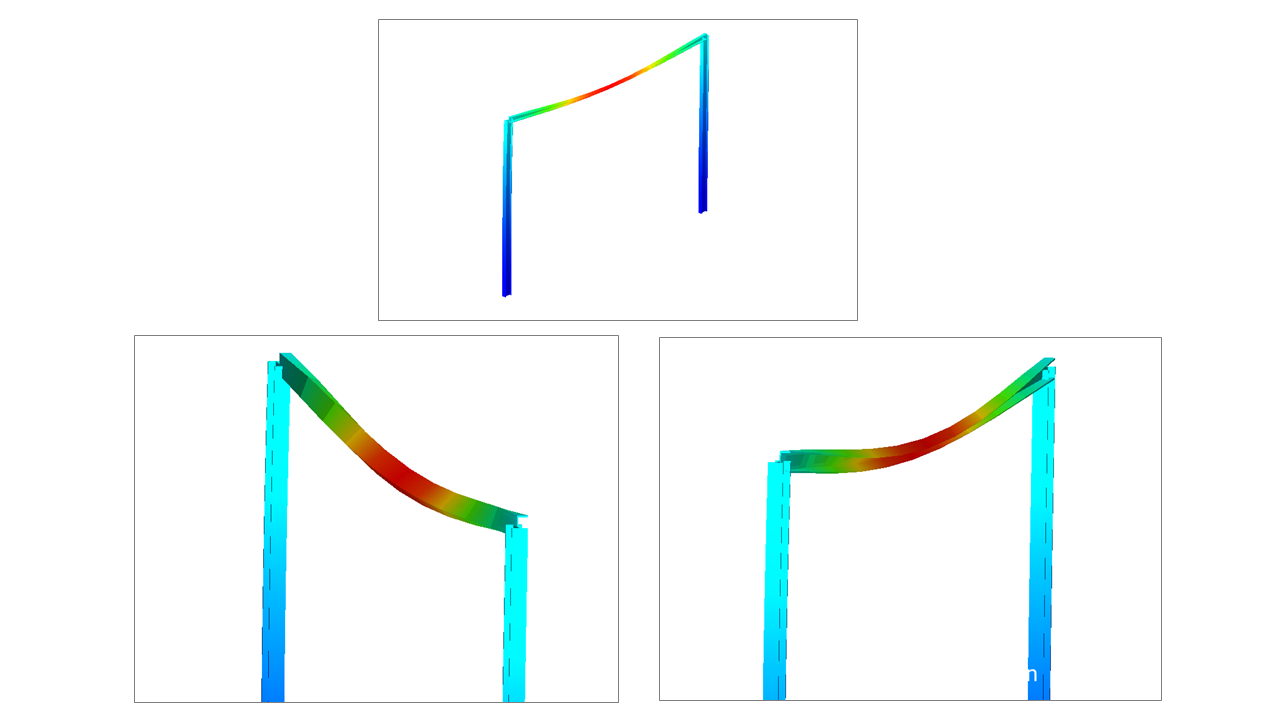
Di seguito il diagramma del momento torcente che sollecita la trave:
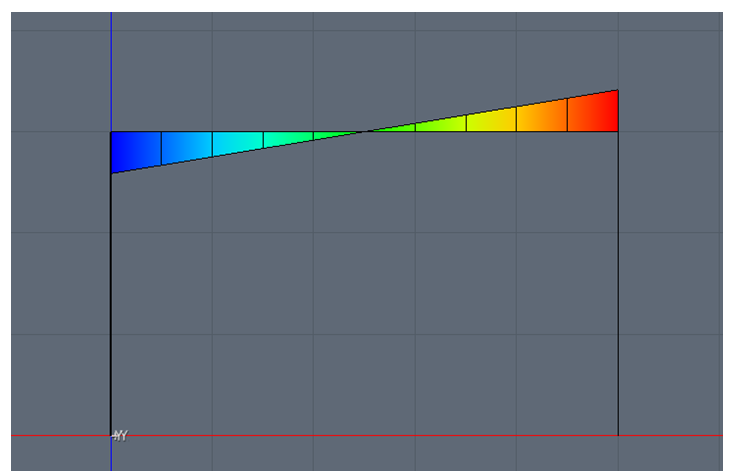
Come hai potuto vedere dalle immagini sopra, la trave si deforma sia con un abbassamento che con una rotazione della sezione. Di conseguenza ci sarà anche il diagramma del momento torcente, che nel caso di un telaio con trave avente sezione doppiamente simmetrica (rettangolare per esempio) non avrebbe modo di esistere.
Conclusioni
Come hai potuto vedere, l’eccentricità fra centro di taglio e baricentro di una sezione produrrà delle sollecitazioni torsionali che rischi di trascurare a causa di un’errata modellazione. Se il profilo ha una lunghezza considerevole, il momento torcente potrebbe raggiungere intensità tali da compromettere il superamento della verifica a torsione.
Quando ti trovi a modellare strutture con sezioni che non sono doppiamente simmetriche ricorda di tener conto del centro di taglio. Ci sono software che portano in conto automaticamente l’eccentricità fra centro di taglio e baricentro della sezione e calcolano di conseguenza il momento torcente sollecitante. Altri software invece richiedono l’inserimento manuale del momento torcente generato come carico applicato all’asta. In entrambi i casi è bene assicurarsi che il momento torcente non comprometta la sicurezza della nostra struttura.
Ti sei mai trovato in una situazione del genere? Come hai modellato l’eccentricità fra centro di taglio e baricentro? Puoi farmelo sapere in un commento all’articolo. Se hai trovato utile il post di oggi puoi consigliarlo ai tuoi amici sul tuo social preferito o ai tuoi colleghi su LinkedIn cliccando sui tasti di condivisione qui sotto.
Al prossimo articolo.
Marco.
Immagini del modellino tratte dal sito della University of Manchester

Salve, e questo effetto torcente che si ha sul traverso a C del telaio dell’esempio si tramuta anche in momento flettente per le colonne in IPE o si chiude all’interno del profilo a C stesso? Me lo domando in quanto per la IPE il carico applicato risulta passante sia per il suo baricentro che per il suo centro di taglio e nei modelli fem (anche quelli che tengono conto in automatico della differenza di posizione tra baricentro e centro di taglio) la IPE non presenta alcun momento flettente.
Grazie, saluti
Ciao Nicola, la tua osservazione è corretta. Il momento torcente nel traverso genera un momento flettente nelle colonne del telaio dell’esempio.
Ciao.
Marco
Pingback:Teoria di Jourawsky: come applicarla senza perdersi in formule [video]