La progettazione di una struttura in calcestruzzo armato solitamente parte dall’elaborazione di una pianta architettonica. E’ compito del progettista strutturale scegliere la posizione in pianta dei pilastri, scegliere l’orientamento del lato lungo e ipotizzare le tipologie di travi di collegamento scegliendo fra trave a spessore o emergente.
In quest’articolo scoprirai i criteri da utilizzare per il posizionamento in pianta dei pilastri e per la scelta dell’orientamento di piatto o di coltello nello schema del telaio. Alla fine del post potrai vedere una video-animazione sul Metodo ReC, il Metodo Ruota e Conta che sono certo ti aiuterà tantissimo nella fase di progettazione di una nuova costruzione. Buona lettura.

Nel corso dell’articolo potrai scaricare gratuitamente Ca.Tel.2D, l’app del blog, implementata in Microsoft Excel, per la risoluzione di schemi statici di qualunque configurazione. I modelli di esempio che vedrai in quest’articolo sono stati creati ed analizzati con l’app Ca.Tel.2D.
Scarica Ca.Tel.2D, l’app per la risoluzione di schemi statici piani (implementata in Microsoft Excel)

Ca.Tel.2D è l’app per la risoluzione di schemi statici piani di qualsiasi configurazione: telai, travature reticolari, capriate, ponteggi metallici etc. L’app è implementata in Microsoft Excel. Puoi scaricare la versione gratuita dell’app compilando i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download.

Posizione dei pilastri in pianta: di piatto o di coltello? Ecco cosa cambia
Sono sicuro che il più delle volte per scegliere l’orientamento di un pilastro ti lasci guidare dallo spessore della tamponatura. Orientare un pilastro di coltello, ovvero con il lato lungo parallelo al piano della parete, ne ridurrà l’ingombro, eliminando l’aggetto dalla tamponatura.
Ho indovinato? Senza dubbio questo è un criterio valido per scegliere l’orientamento di un pilastro, ma non è l’unico che puoi utilizzare. Ce ne sono altri che hanno un significato ben più importante ai fini del comportamento sismico globale di una struttura. Te li mostro di seguito. Continua a leggere.
Posizionare un pilastro di piatto o di coltello non ha effetto solo sull’ingombro in pianta. Ruotare l’orientamento di un pilastro vuol dire modificare la rigidezza traslante dell’intera pilastrata e del telaio a cui il pilastro appartiene.
La rigidezza flessionale di un pilastro dipende dal modulo elastico del materiale, dal momento di inerzia della sezione e dalla lunghezza dell’asta. Ti mostro un caso semplice: un telaio shear-type ovvero con traverso infinitamente rigido. In questo caso i nodi di estremità del pilastro possono soltanto traslare, le rotazioni dei nodi di estremità invece sono impedite. Nell’immagine seguente puoi vedere la differenza fra l’orientamento di coltello e di piatto dei pilastri.
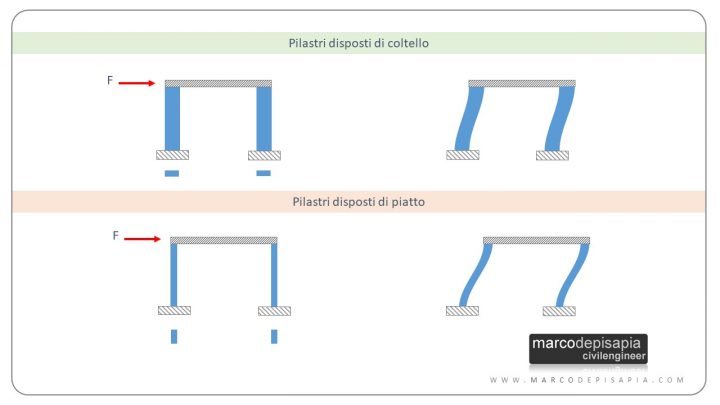
Il contributo di ciascun ritto alla rigidezza traslante del telaio è dato dalla formula seguente:
K = 12 ∙ E ∙ I / L3
- E = modulo elastico della sezione;
- I = momento d’inerzia della sezione;
- L = lunghezza dell’asta.
Cambiare l’orientamento di un pilastro, ruotando la sua sezione, equivale a cambiare il valore del momento di inerzia nella formula della rigidezza e di conseguenza modificare la rigidezza traslante del telaio cui l’asta appartiene.
Un esempio numerico:
- Pilastro 30×70, orientamento di coltello ⇒ momento d’inerzia = b ∙ h3/12 = 30 ∙ 703/12 = 857’500 cm4
- Pilastro 70×30, orientamento di piatto ⇒ momento d’inerzia = h ∙ b3/12 = 70 ∙ 303/12 = 157’500 cm4
Ruotando un pilastro di sezione 30×70, il momento d’inerzia aumenta di circa 6 volte passando da un orientamento di piatto ad un orientamento di coltello.
Lo stesso discorso fatto per i pilastri vale per le travi, a seconda che si tratti di una trave emergente o a spessore. La trave emergente avrà di conseguenza una rigidezza flessionale nettamente superiore rispetto alla trave a spessore.
Pilastri di piatto o di coltello e travi emergenti o a spessore possono essere accoppiati fra loro in diverse combinazioni. Cosa succede quando si combinano pilastri di piatto o di coltello con travi emergenti o a spessore? Te lo mostro di seguito con degli esempi pratici.
Rigidezza del telaio: pilastri di piatto o di coltello, travi emergenti o a spessore.
Per mostrarti cosa cambia nei confronti dell’azione orizzontale a seconda di come si combinano fra loro pilastri e travi, ti mostro un esempio pratico di un telaio a tre livelli e tre campate, di altezza 3 metri per ciascun livello e di luce 5 metri per ciascuna campata. I pilastri hanno tutti una sezione rettangolare 30×70.
Gli esempi che ti mostro di seguito sono stati modellati utilizzando Ca.Tel.2D, l’app del blog per la risoluzione di schemi statici piani di qualsiasi configurazione. Per valutare la rigidezza traslante nei diversi casi, il telaio è stato caricato all’ultimo livello da una forza orizzontale di 100 kN. In ogni esempio viene valutato lo spostamento orizzontale del nodo di sommità per poter valutare la rigidezza traslante del telaio.
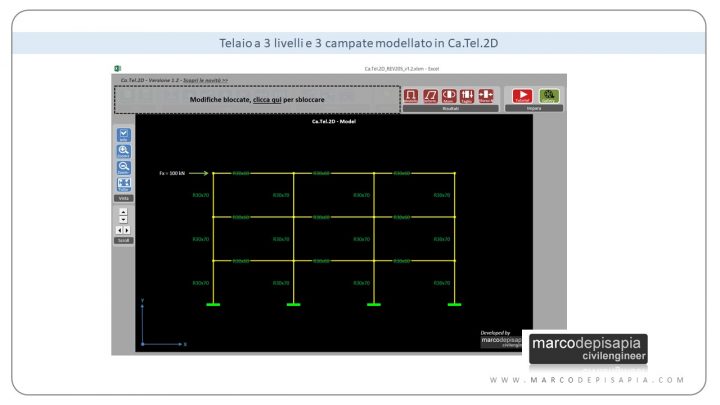
Negli esempi di seguito, è stata ruotata una pilastrata per volta, passando da un orientamento di coltello ad un orientamento di piatto. Le diverse combinazioni ottenute per l’orientamento delle pilastrate sono state ripetute una volta nel caso di travi di collegamento tutte emergenti 30×60 e poi con travi di collegamento a spessore 80×22. Seguiranno una serie di immagini delle deformate dei telai per ciascuna combinazione analizzata. Più in fondo troverai una tabella di riepilogo dei risultati ottenuti.
4 pilastri di coltello + travi emergenti
In quest’esempio tutti i pilastri 30×70 sono stati posizionati di coltello e sono collegati fra loro da travi emergenti 30×60.
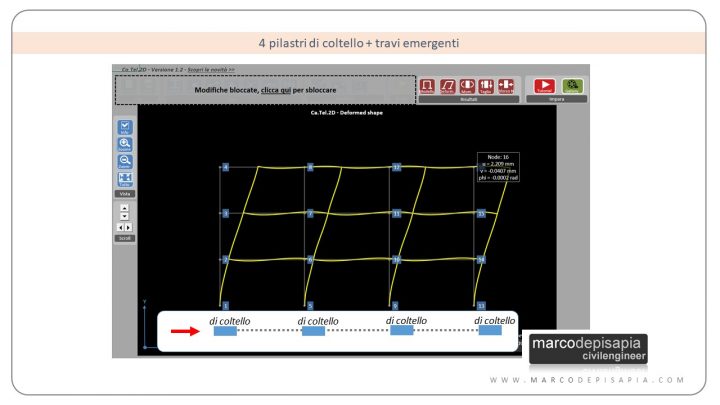
3 pilastri di coltello e 1 pilastro di piatto + travi emergenti
L’orientamento della seconda pilastrata viene variato, ruotando il pilastro e posizionandolo di piatto. Le travi continuano ad essere tutte emergenti.
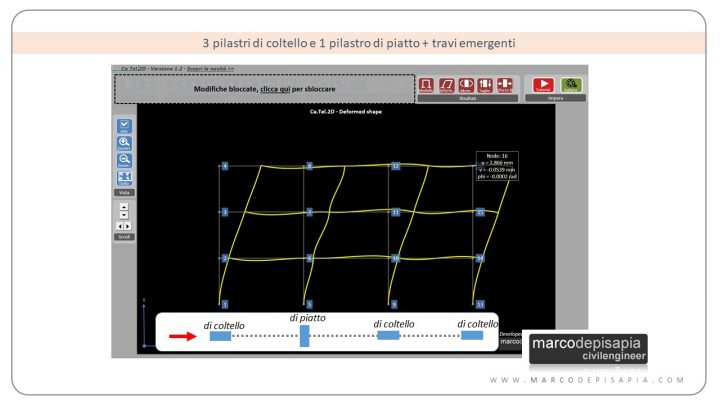
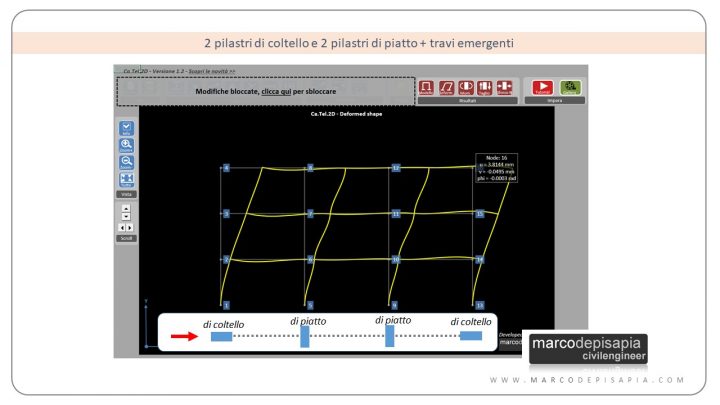
2 pilastri di coltello e 2 pilastri di piatto + travi emergenti
Le due pilastrate centrali sono state orientate di piatto.
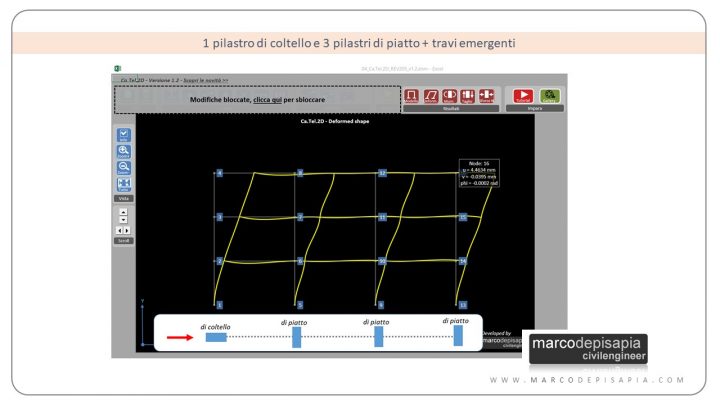
1 pilastro di coltello e 3 pilastri di piatto + travi emergenti
3 pilastrate su 4 sono orientate di piatto.
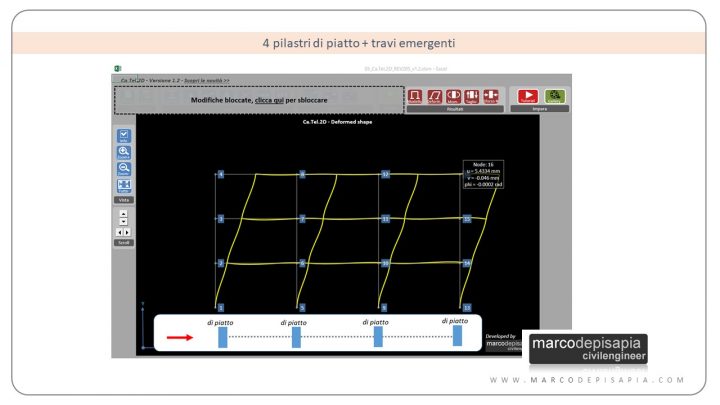
4 pilastri di piatto + travi emergenti
In quest’esempio tutte le pilastrate sono orientate di piatto.
Nelle immagini seguenti vengono ripetuti i 5 casi precedenti con una differenza: le pilastrate sono collegate fra loro con travi a spessore di sezione 80×22.
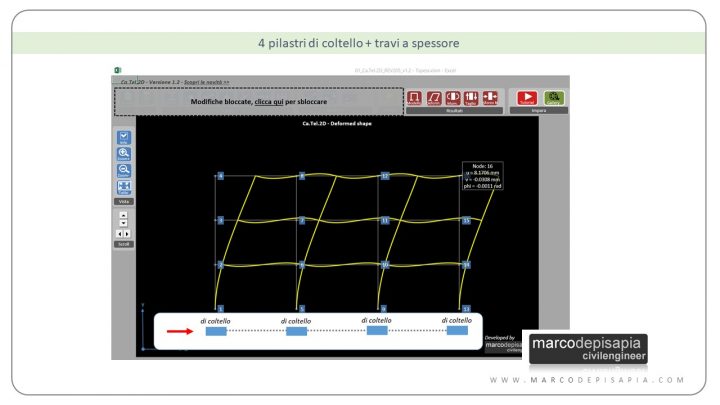
Pilastri di coltello + travi a spessore
3 pilastri di coltello e 1 pilastro di piatto + travi a spessore
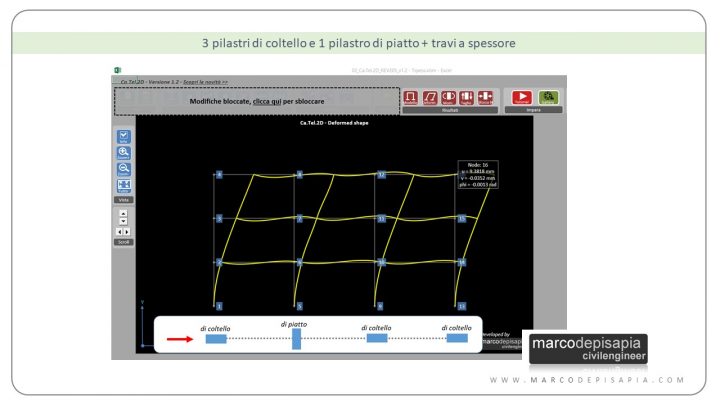
2 pilastri di coltello e 2 pilastri di piatto + travi a spessore
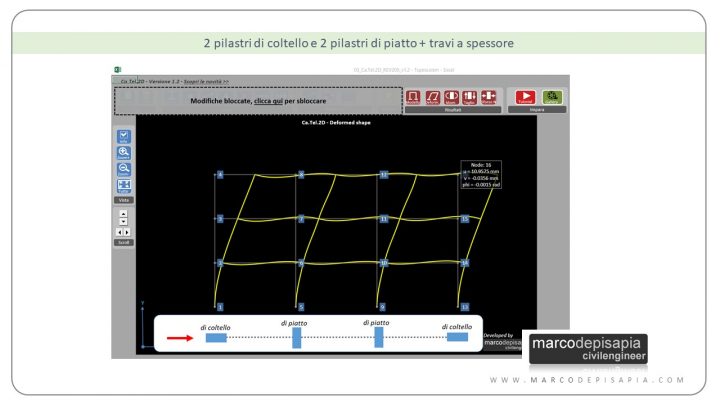
1 pilastro di coltello e 3 pilastri di piatto + travi a spessore
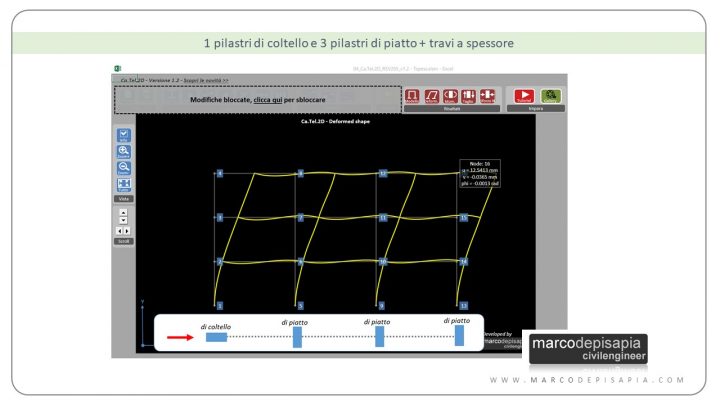
4 pilastri di piatto + travi a spessore
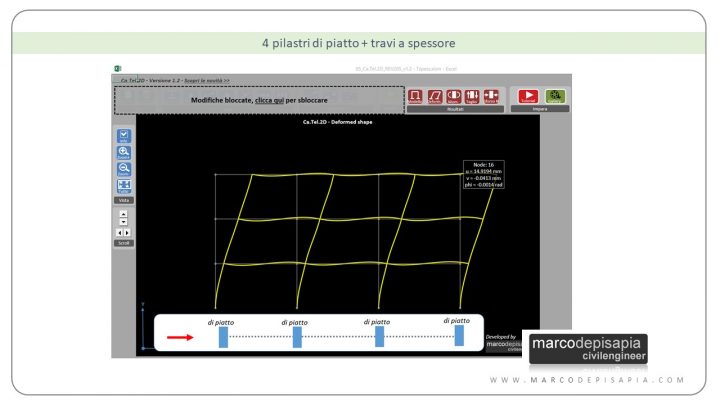
Riepilogo dei risultati
Riassumendo tutti i risultati ottenuti diventa evidente come la rigidezza del telaio sia fortemente influenzata dall’orientamento delle pilastrate e dal loro accoppiamento con travi emergenti o a spessore. Ti riporto di seguito una tabella di riepilogo con i valori degli spostamenti del nodo di sommità e delle rigidezze traslanti per ciascun caso.
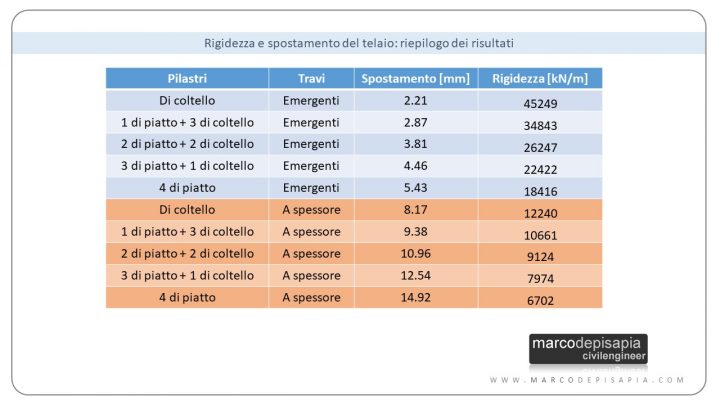
Nell’immagine che segue ti riporto un grafico a barre che riassume i valori delle rigidezze traslanti.
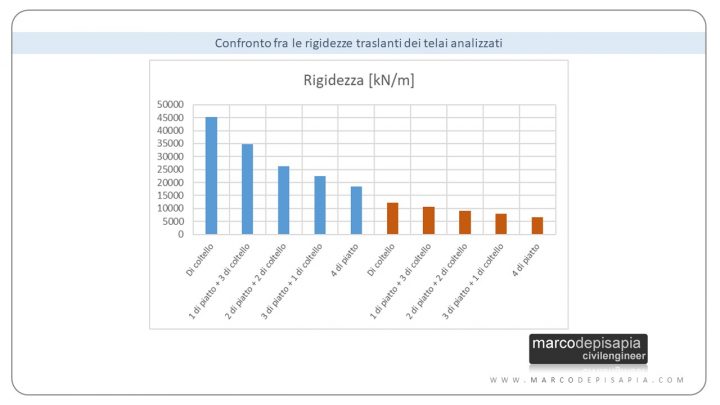
Come puoi vedere dal grafico sopra, quando le pilastrate sono collegate da travi a spessore, la rigidezza traslante si abbatte drasticamente (barre di colore arancione), riducendosi di oltre un terzo rispetto allo schema analogo con travi emergenti. Questo è uno dei motivi per cui la Normativa Tecnica prescrive di non utilizzare telai sismo-resistenti con travi a spessore nel caso in cui si progetti in classe di duttilità Alta (CD”A”).
Come hai potuto vedere, gli orientamenti dei pilastri e l’accoppiamento con travi emergenti o a spessore influiscono sulla rigidezza traslante del telaio. Nell’ambito del comportamento sismico globale di una struttura, vale la seguente regola: i telai più rigidi sono quelli che assorbono la maggiore aliquota dell’azione sismica. Se in una stessa struttura c’è un telaio con tutti i pilastri di piatto collegati da travi a spessore, mentre quello immediatamente adiacente ha tutti i pilastri di coltello collegati da travi emergenti, sarà quest’ultimo che assorbirà le sollecitazioni maggiori rispetto al precedente.
La rigidezza dei diversi telai gioca un ruolo importante anche sotto un altro aspetto: la posizione del baricentro delle rigidezze. Ti ho già parlato in quest’articolo della differenza che esiste fra il baricentro delle masse di un impalcato e il baricentro delle rigidezze e del ruolo che gioca la distanza fra questi due baricentri.
Un ultimo fattore che influisce sulla rigidezza dei telai è la luce delle campate. A parità di sezioni di pilastri e travi infatti, modificando le luci, cambierà la rigidezza del telaio. Diminuendo la luce aumenterà la rigidezza. Viceversa aumentando la luce, diminuirà la rigidezza. Questo perché la rigidezza flessionale delle travi di collegamento dipende dalla loro lunghezza. In pratica un altro elemento su cui puoi agire se vuoi modificare la rigidezza dei telai è l’interasse dei pilastri e quindi la luce delle campate.
Scarica Ca.Tel.2D l’app per la risoluzione di schemi statici piani
Ca.Tel.2D è l’app del blog per la risoluzione di schemi statici piani di qualsiasi configurazione: telai, travature reticolari, capriate, ponteggi metallici etc. I modelli di esempio riportati in quest’articolo sono stati creati e analizzati con Ca.Tel.2D. Per scaricare gratuitamente l’app, compila i campi qui sotto, riceverai all’istante una email contenente il link per eseguire il download.

Posizione dei pilastri: progetta la tua struttura con il metodo ReC – Ruota e Conta
Abbiamo visto finora come l’orientamento dei pilastri e la tipologia di trave influisce sulla rigidezza di un telaio piano. Ragionando su un singolo telaio sembra tutto abbastanza semplice, ma tenere in considerazione questi elementi durante la progettazione di una struttura è un po’ più complesso.
Per una struttura tridimensionale ciascuna pilastrata sarà orientata di piatto per un telaio e di coltello per il telaio in direzione ortogonale. Sarà l’abilità del progettista strutturale a trovare la giusta combinazione di orientamenti e accoppiamenti con le travi per garantire il migliore comportamento della struttura. Il tutto rispettando i vincoli architettonici (ingombro in pianta, necessità di travi a spessore di solaio, luci delle campate etc.).
Nella parte finale di quest’articolo voglio fornirti un metodo pratico che puoi utilizzare per bilanciare la distribuzione delle rigidezze agendo sull’orientamento dei pilastri. Si tratta del Metodo ReC: Ruota e Conta.
Questo metodo consiste nel considerare le direzioni principali X e Y e contare i pilastri di coltello in ciascuna direzione. Per ottenere una buona distribuzione di rigidezza i pilastri di coltello devono essere uguali in numero (o se non proprio uguali almeno confrontabili) nelle due direzioni X e Y e distribuiti uniformemente lungo i lati della pianta. Ti mostro un esempio del Metodo ReC nell’immagine seguente e nel video che trovi di seguito.
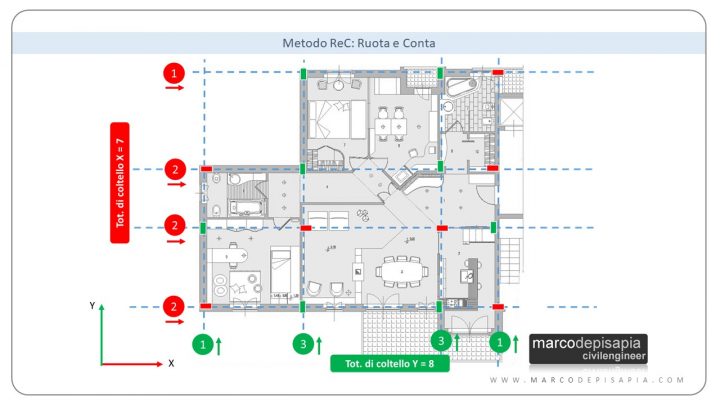
Guarda il video sull’applicazione del Metodo ReC per progettare la posizione e l’orientamento dei pilastri
In questo video ti mostro l’applicazione pratica del Metodo ReC per scegliere l’orientamento in pianta dei pilastri. Buona visione.
Posizione pilastri: conclusioni
Quest’articolo finisce qui. Spero di averti fornito delle informazioni utili da utilizzare quando progetti una struttura o magari quando devi valutare se una struttura esistente è stata ben concepita, prima ancora di mettere mano al tuo software di calcolo. Se hai trovato utile questo post, puoi suggerirlo ai tuoi colleghi su Linkedin o ai tuoi amici su Facebook cliccando sui tasti di condivisione in fondo alla pagina.
Al prossimo articolo.
Marco
Ultimo aggiornamento: 20/1/2023. Pubblicato il 16/10/2017. – Codice articolo: 216

Ciao Marco leggo spesso e con attenzione i tuoi articoli, avrei una domanda da farti relativamente a:
– nell’adeguamento di una struttura in c.a. è stato previsto di realizzare dei telai irrigidenti esterni in c.a. composti da trave di fondazione, setti verticali in corrispondenza dei pilastri esistenti e travi di collegamento fra i setti, il tutto da ancorare alla struttura esistente in c.a.
DOMANDA: trattandosi di una scuola in esercizio, e con temi limitati per l’esecuzione dei lavori, volendo limitare le lavorazioni dei setti e travi in c.a. (Setti dim. 30*70, travi 25*70 e controfondazioni a L120*50) casseformi, armature e getti, CONSIGLIERESTI la sostituzione con un telaio in acciaio più facile e più veloce nel montaggio?
grazie walter
Ciao Rizzo,
il telaio in acciaio potrebbe essere una valida alternativa per velocizzare la realizzazione a patto di garantire la stessa rigidezza del telaio in c.a., magari mediante l’utilizzo di opportuni controventi, e il soddisfacimento delle verifiche di resistenza.
Pingback:Come progettare una struttura con il Metodo ReC (Ruota e Conta) [video]