In passato, quando non esistevano computer e software di calcolo, era di fondamentale importanza per un ingegnere strutturista saper utilizzare metodi veloci e pratici per risolvere problemi ingegneristici. Uno di questi è senz’altro la costruzione del Cerchio di Mohr. Si tratta di un procedimento grafico ideato nel 1882 dall’ingegner Christian Otto Mohr.
Il cerchio di Mohr consente di rappresentare lo stato tensionale piano in un punto di un corpo e conoscere le tensioni che agiscono su una giacitura di qualsiasi inclinazione, evitando di eseguire calcoli numerici e procedendo solo per costruzioni grafiche.
In quest’articolo ti mostro come si costruisce il cerchio di Mohr e soprattutto qual è la sua utilità. Alla fine dell’articolo troverai un video esplicativo in cui potrai visualizzare, grazie a delle animazioni, tutti i passaggi della costruzione grafica. Non perdertelo.
Il piano di Mohr
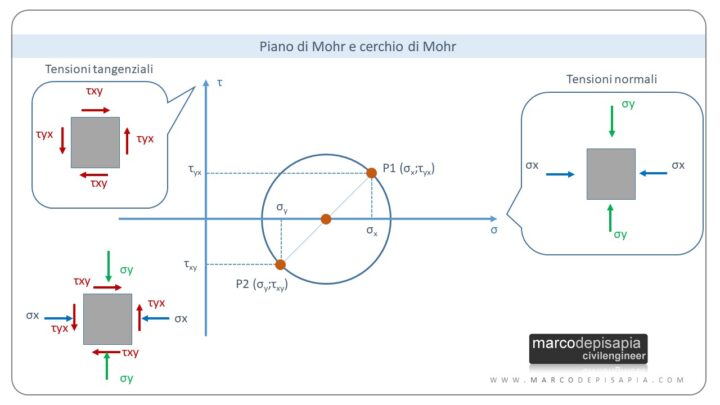
Il piano di Mohr è un piano cartesiano composto dall’asse delle ascisse su cui vengono rappresentate le tensioni normali σ e dall’asse delle ordinate su cui vengono riportate le tensioni tangenziali τ.
Il cerchio di Mohr è utilizzato per rappresentare graficamente lo stato piano di tensione interna in un punto di un corpo. Dato uno stato tensionale individuato dalle tensioni normali e tangenziali, è possibile tracciare il cerchio riportando nel piano i valori delle tensioni agenti sulla giacitura verticale e orizzontale.
Costruzione del cerchio di Mohr: caso di sole tensioni normali agenti
Per costruire il cerchio di Mohr si riportano nel piano le tensioni normali e tangenziali che agiscono sulla giacitura orizzontale e verticale.
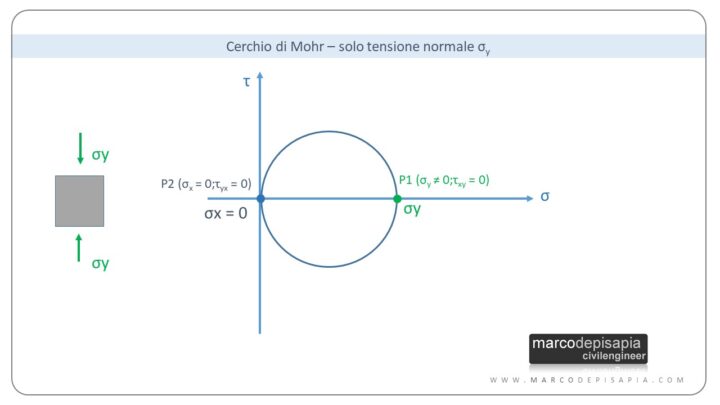
Nel caso in cui agisca la sola tensione verticale σy sulla giacitura orizzontale e le σx e le τ siano nulle, riportando nel piano di Mohr i punti P1 (σy ≠ 0; τxy = 0) per la giacitura orizzontale e P2 (σx = 0; τyx = 0) per la giacitura verticale, sarà noto il diametro e di conseguenza sarà possibile tracciare il cerchio di Mohr.
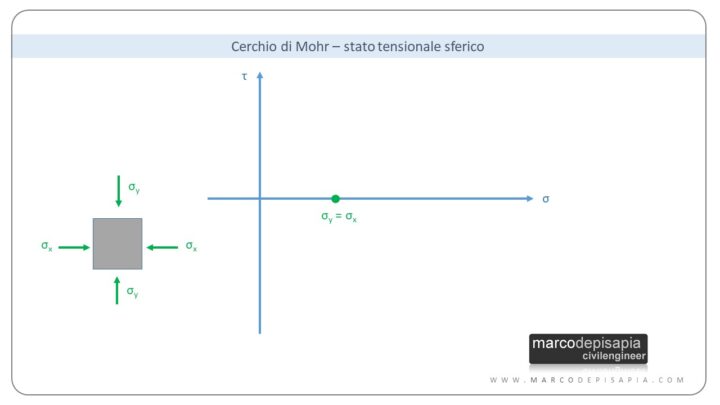
Se la σx e la σy sono coincidenti e non agirà alcuna tensione tangenziale, il cerchio di Mohr degenera in un punto. Si avrà uno stato tensionale sferico, ovvero di sole tensioni normali.
Costruzione del cerchio di Mohr: caso di sole tensioni tangenziali agenti
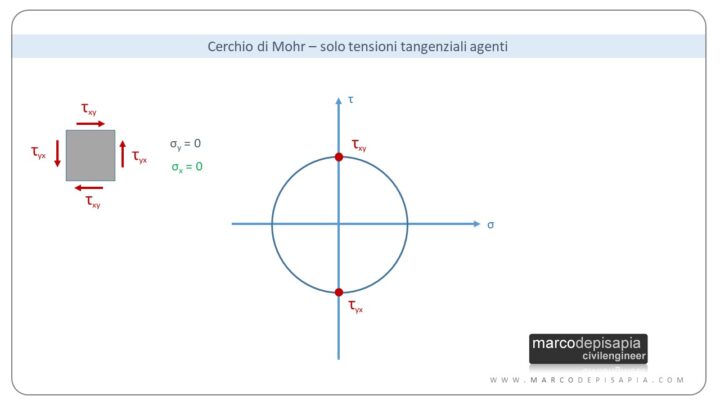
Nel caso in cui agisca la sola tensione tangenziale τ, si riportano nel piano i punti P1 (σy = 0; τxy ≠ 0) per la giacitura orizzontale e P2 (σx = 0; τyx ≠ 0) per la giacitura verticale. Il diametro sarà individuato dai due punti corrispondenti e sarà possibile tracciare il cerchio di Mohr.
Costruzione del cerchio di Mohr: tensioni normali e tangenziali agenti
Se agiscono sia le tensioni normali che tangenziali sulle giaciture orizzontali e verticali, si riportano nel piano i valori delle tensioni normali e tangenziali per ciascuna giacitura per individuare il diametro del cerchio. Pertanto si rappresenteranno nel piano di Mohr i punti P1 (σy ≠ 0; τxy ≠ 0) per la giacitura orizzontale e P2 (σx ≠ 0; τyx ≠ 0) per la giacitura verticale.
Cerchio di Mohr: individuazione del polo
Il cerchio di Mohr consente di individuare lo stato tensionale per qualsiasi orientamento della giacitura. Per poter individuare lo stato tensionale di una giacitura, bisogna individuare il polo del cerchio di Mohr. Per determinare il polo è sufficiente tracciare una retta orizzontale passante per il punto del cerchio individuato dallo stato tensionale che agisce sulla giacitura orizzontale.
Allo stesso modo si traccerà una retta verticale passante per il punto del cerchio individuato dallo stato tensionale che agisce sulla giacitura verticale. L’intersezione di queste due rette individua il polo del cerchio di Mohr.
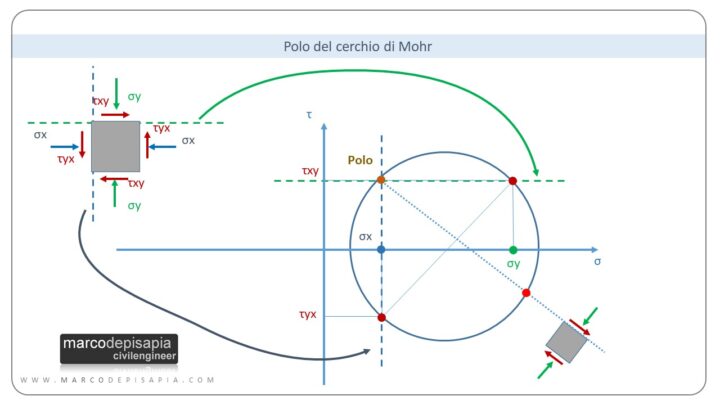
Tracciando una retta con una qualunque inclinazione a partire dal polo, possiamo conoscere lo stato tensionale agente sulla giacitura avente l’inclinazione corrispondente. Lo stato tensionale agente sulla giacitura sarà dato dall’intersezione della retta con il cerchio di Mohr.
Rappresentazione di uno stato tensionale su una qualunque giacitura
Grazie al cerchio di Mohr è possibile ricavare lo stato tensionale agente su una giacitura di qualunque inclinazione e individuare le direzioni principali di tensione, ovvero quelle giaciture su cui agiscono solo le tensioni normali, mentre le tensioni tangenziali sono nulle.
Se un materiale raggiunge la rottura per effetto della tensione tangenziale agente, come accade per esempio per il calcestruzzo, dal cerchio di Mohr possiamo determinare la massima tensione verticale che porta a rottura il materiale. La rottura avverrà sulla giacitura inclinata a 45° su cui si avrà la massima tensione tangenziale.
Il cerchio di Mohr può essere utilizzato ad esempio per comprendere l’effetto del confinamento del calcestruzzo generato da staffe e legature, in grado di incrementare la resistenza a compressione del calcestruzzo. Grazie a questa costruzione grafica possiamo renderci conto dell’effetto prodotto dalla pressione laterale di confinamento ovvero l’incremento della massima tensione verticale che porta a rottura il materiale.
Guarda il video sul cerchio di Mohr (clicca su PLAY)
Ti riporto di seguito la versione video di quest’articolo. Buona visione.
Conclusioni
Il cerchio di Mohr è un utile metodo grafico che consente di rappresentare in modo semplicissimo qualunque stato piano di tensione in un corpo. A primo impatto l’utilizzo di questo metodo grafico potrebbe sembrare complesso. Spero che quest’articolo abbia contribuito a fare chiarezza.
Se questo nuovo video ti è piaciuto, puoi suggerirlo ai tuoi colleghi su Linkedin e ai tuoi amici su Facebook cliccando sui tasti di condivisione social che trovi in fondo alla pagina.
Per ricevere gli ultimi articoli e risorse direttamente nella tua casella email iscriviti alla newsletter del blog. Se non sei ancora iscritto, puoi completare l’iscrizione compilando i campi qui sotto. Riceverai subito un’email per il download di quattro applicazioni utili per il calcolo strutturale.
Per non perderti la pubblicazione di nuovi video, iscriviti al canale YouTube al link seguente:
Iscriviti al canale YouTube >>
Al prossimo articolo.
Marco
Ultimo aggiornamento: 16/1/2022. Pubblicato il 4/6/2018.

Corpi rigidi o deformabili? Mi sono sempre chiesto se nel cerchio di
Mohr quando si tratta di tensioni si faccia o meno riferimento alla
deformabilità!
In molte applicazioni è citato un trasposto del cerchiodi Mohr, indicato come “arbelo di Mohr” (per corpi deformabili).
Si tratta di un grafico piano in cui vengono rappresentate le “tre” tensioni principali: sigma1, sigma2 e sigma3.
In sostanza ci si riferisce a uno stato triassiale: anche nella Meccanica delle Terre gli stati di sollecitazione possono essere triassiali (vedi p.e. prove TX su
campioni indisturbati).
Leggendo, poi si trova che “arbelo” dovrebbe essere una figura piana (già studiata da Archimede) delimitata da tre cerchi (o tre circonferenze).
Quindi il cerchio di Mohr (molto interessante!) di per sé finisce per offrire anche molto di più, potendosi riferire anche a “stati triassiali” …
Ignoro il motivo per cui il c.d. “arbelo” venga tirato in ballo con la “deformabilità” (in
Meccanica lo studio della deformabilità è fondamentale anche per certe
lavorazioni, dette appunto “plastiche”).
Ciao Giuseppe, grazie del commento. I tuoi spunti di riflessione sono molto interessanti. In effetti il cerchio di Mohr può essere utilizzato per rappresentare stati tensionali triassiali, ottenendo in tal modo l'”arbelo”. Ciao. Marco
Pingback:Resistenza nel piano dei maschi murari: meccanismi di rottura