Scala in cemento armato: come posizionarla in pianta per le costruzioni in zona sismica

Il posizionamento in pianta del corpo scala in cemento armato va valutato con attenzione in fase di progetto di un edificio. La struttura del corpo scala, realizzata con solette rampanti o con travi a ginocchio, altera il reticolo spaziale a maglie rettangolari delle strutture intelaiate, modificando significativamente la posizione in pianta del baricentro delle rigidezze.

In quest’articolo vedremo tutti gli elementi di irregolarità che la scala in cemento armato introduce in una struttura intelaiata, ti mostrerò in che modo la struttura della scala riduce gli spostamenti relativi di interpiano e come realizzare una scala che abbia un impatto minimo sulla regolarità strutturale utilizzando il modello proposto dall’ing. Aurelio Giliberti (da cui il nome di scala alla Giliberti).

Nel corso dell’articolo troverai dei consigli per il corretto posizionamento in pianta della scala in cemento armato per una nuova costruzione, in modo da modificare in maniera minima il comportamento dinamico della struttura in presenza dell’azione sismica. Alla fine del post potrai scaricare gratuitamente un opuscolo illustrativo sul modello di scala alla Giliberti. Buona lettura.

Scala in cemento armato: l’incremento di rigidezza del telaio

Nell’immagine seguente ti mostro una tipica configurazione di scala a soletta rampante.

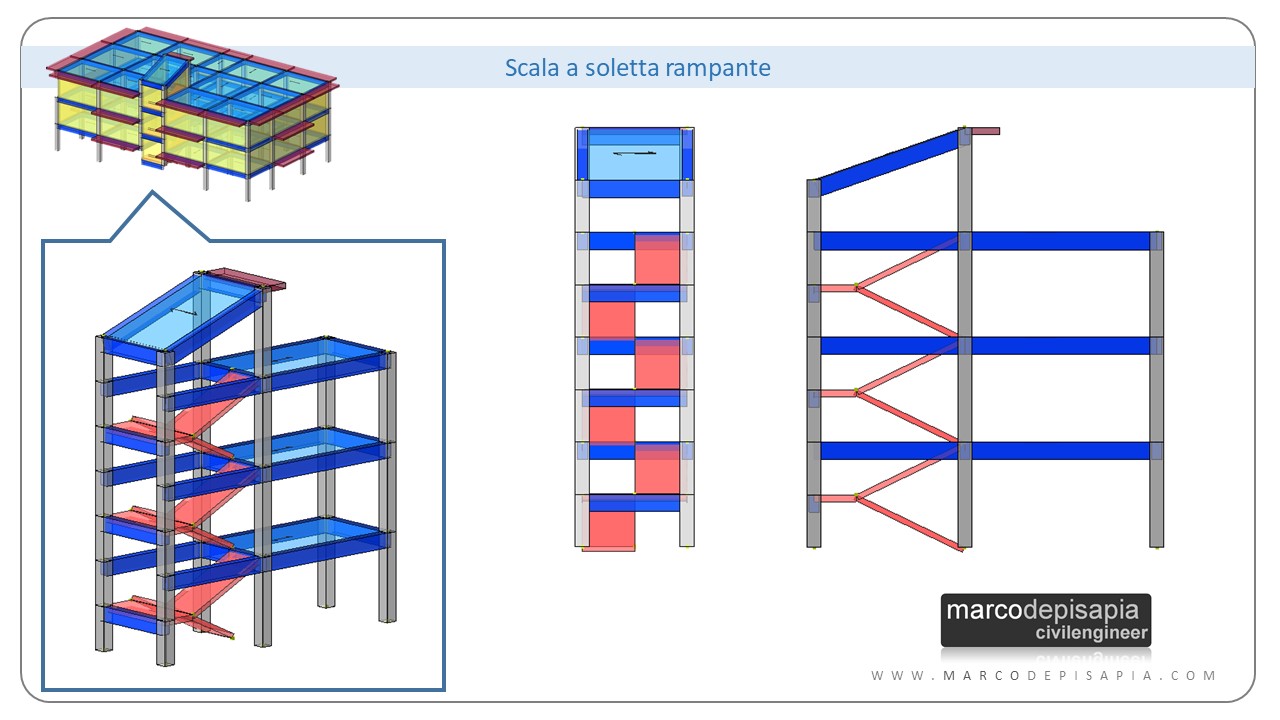
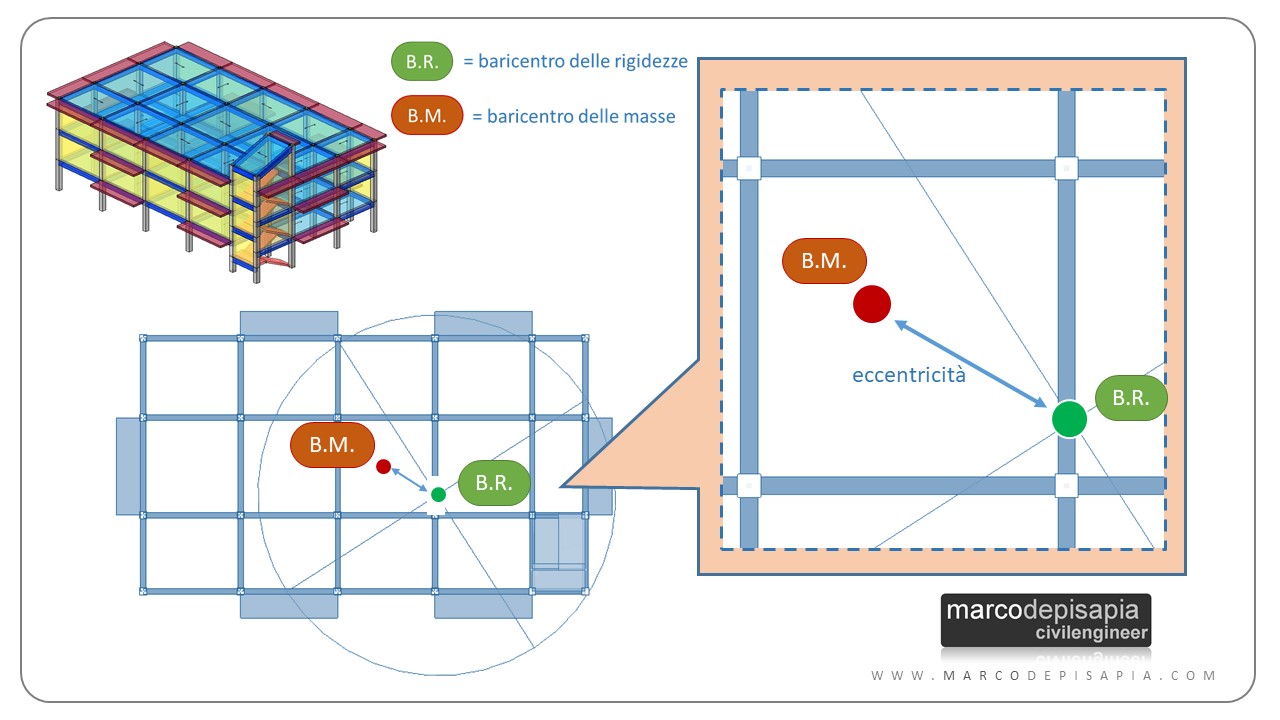
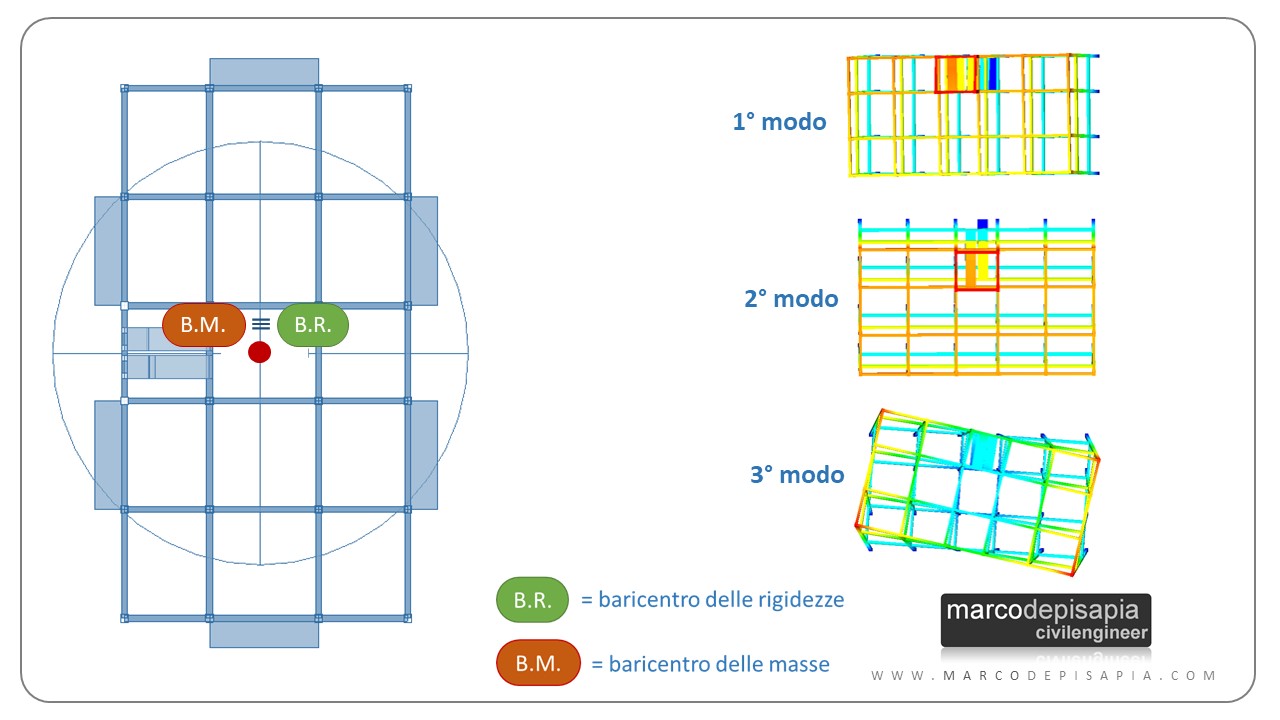
Il primo effetto della presenza della scala è lo spostamento del baricentro delle rigidezze della struttura. Il baricentro delle rigidezze si avvicinerà al corpo scala, allontanandosi dal baricentro delle masse. Nell’immagine seguente puoi vedere come, per un edificio a pianta rettangolare, il baricentro delle rigidezze sia spostato verso il corpo scala, generando eccentricità rispetto al baricentro delle masse. 

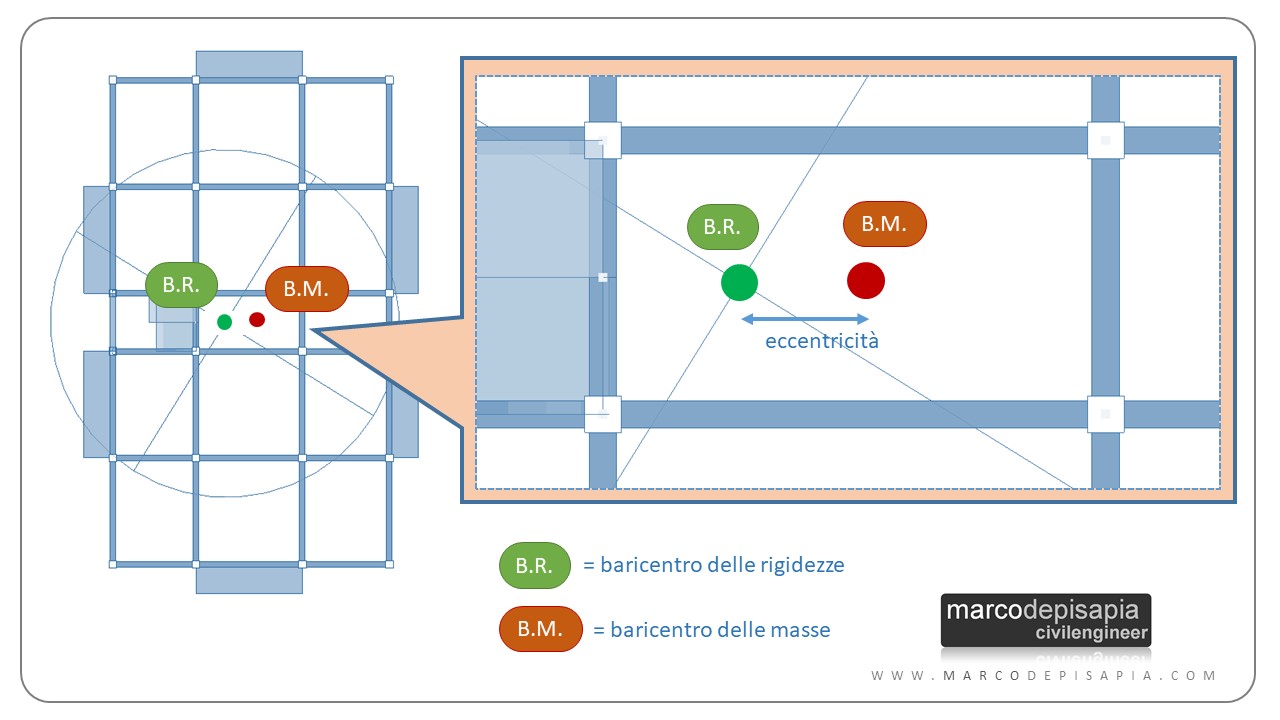
Per analizzare l’influenza del corpo scala sull’eccentricità fra baricentro delle masse e delle rigidezze, nel modello analizzato ho inserito pilastri a sezione quadrata. In tal modo l’orientamento di piatto o di coltello dei pilastri, non influisce sulla posizione del baricentro delle rigidezze. Ho inoltre trascurato l’eccentricità accidentale del 5% per il baricentro delle masse prescritta dalle NTC2018. 

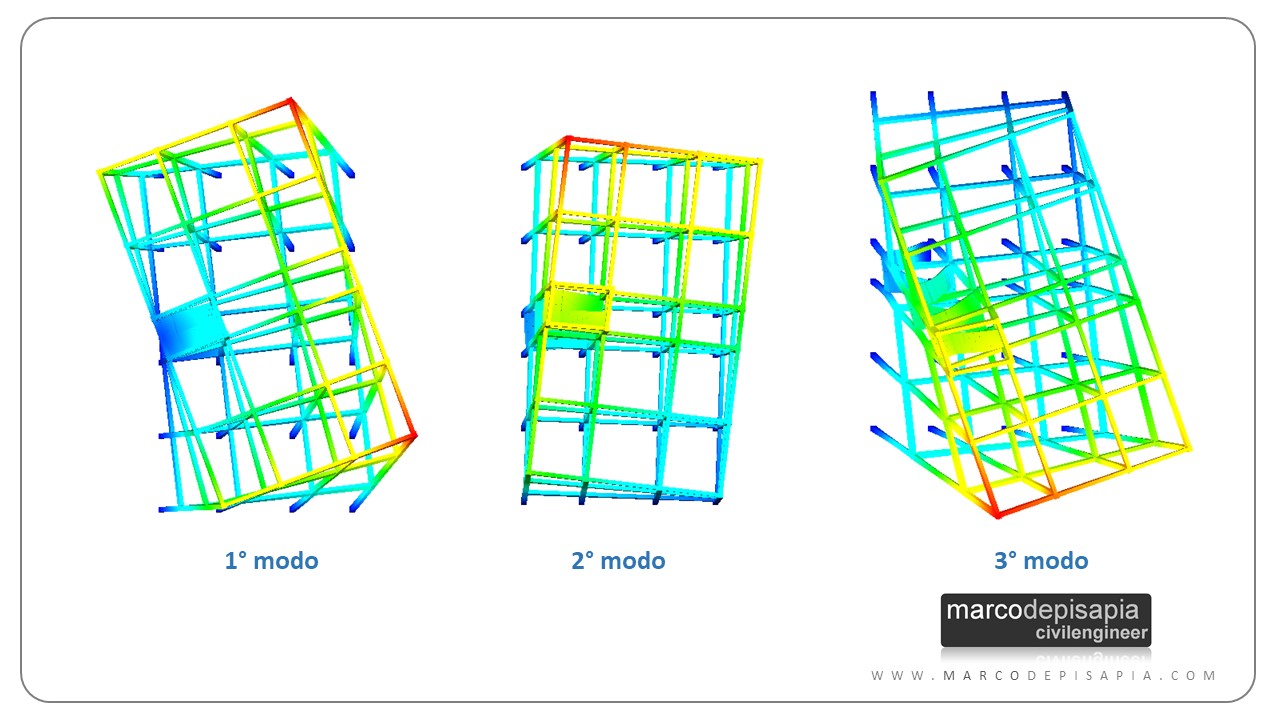
L’eccentricità fra baricentro delle masse e delle rigidezze darà vita a rotazioni torsionali degli impalcati. Lo puoi vedere dalla configurazione dei primi tre modi di vibrare nell’immagine seguente. Il primo e il secondo modo dovrebbero essere puramente traslazionali in direzione X e Y. La presenza del corpo scala genera delle componenti rotazionali nei primi due modi di vibrare.

Perché il corpo scala sposta il baricentro delle rigidezze

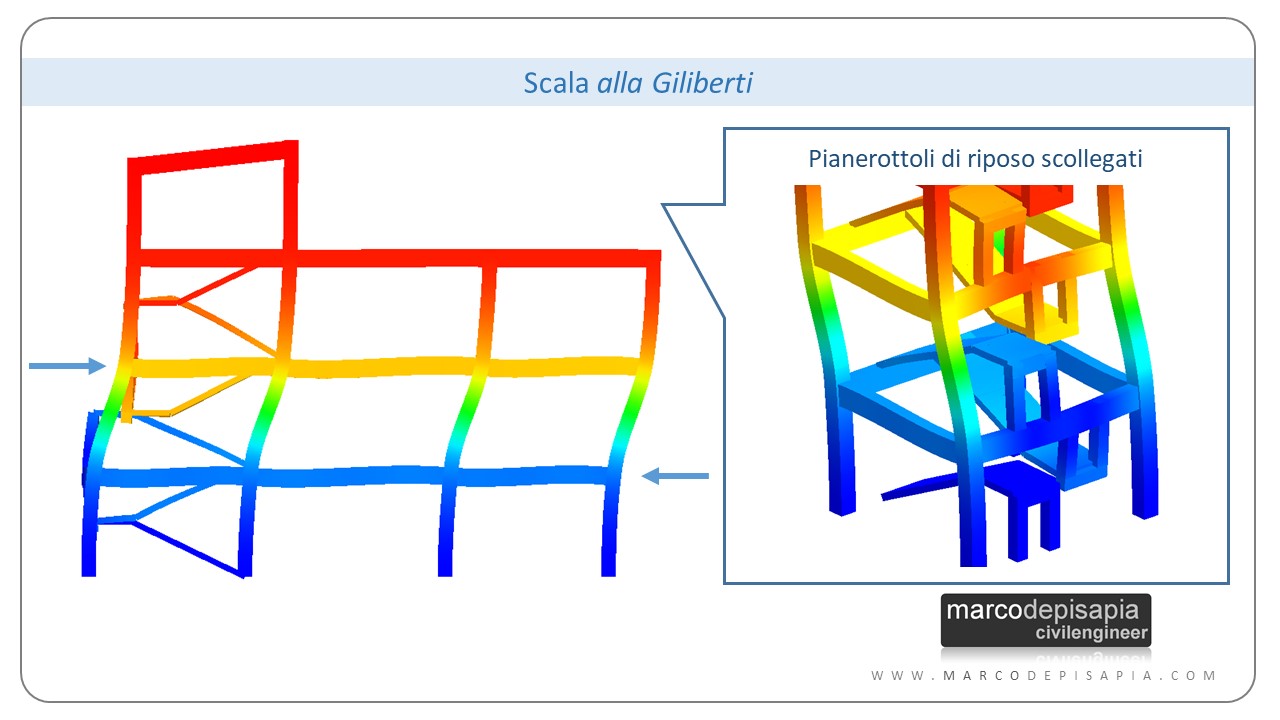
L’influenza del corpo scala sulla posizione del baricentro delle rigidezze è dovuta alla presenza delle travi dei pianerottoli di riposo. Tali travi si trovano ad una quota intermedia fra la quota dell’impalcato inferiore e superiore, dimezzando la lunghezza di libera inflessione dei pilastri a cui si collegano. 

I pilastri intercettati dalle travi dei pianerottoli di riposo saranno pilastri tozzi, con un’altezza dimezzata rispetto agli altri pilastri della struttura e pertanto con una rigidezza flessionale circa 8 volte maggiore (se si prende come riferimento un’asta incastrata-incastrata) rispetto ai restanti pilastri.

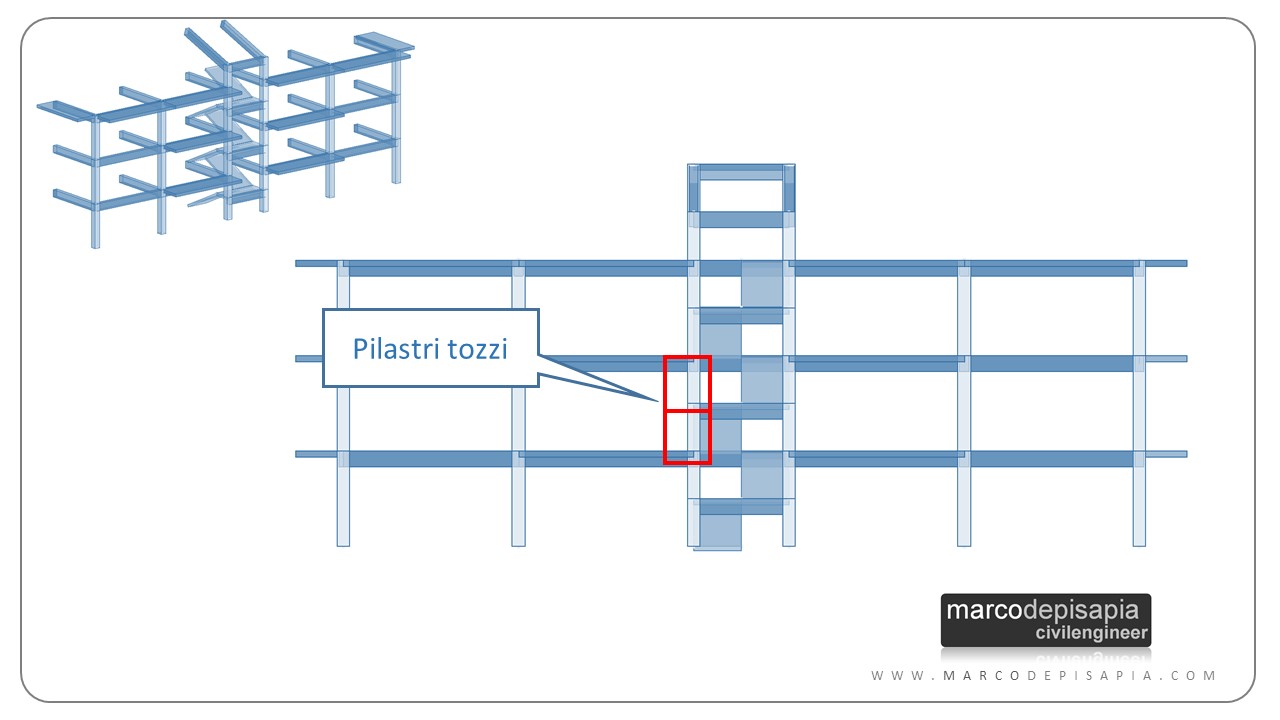
Puoi renderti conto della maggiore rigidezza del telaio che contiene le travi di pianerottolo dall’immagine seguente.  I due telai sono stati caricati con forze orizzontali di piano della stessa intensità. 

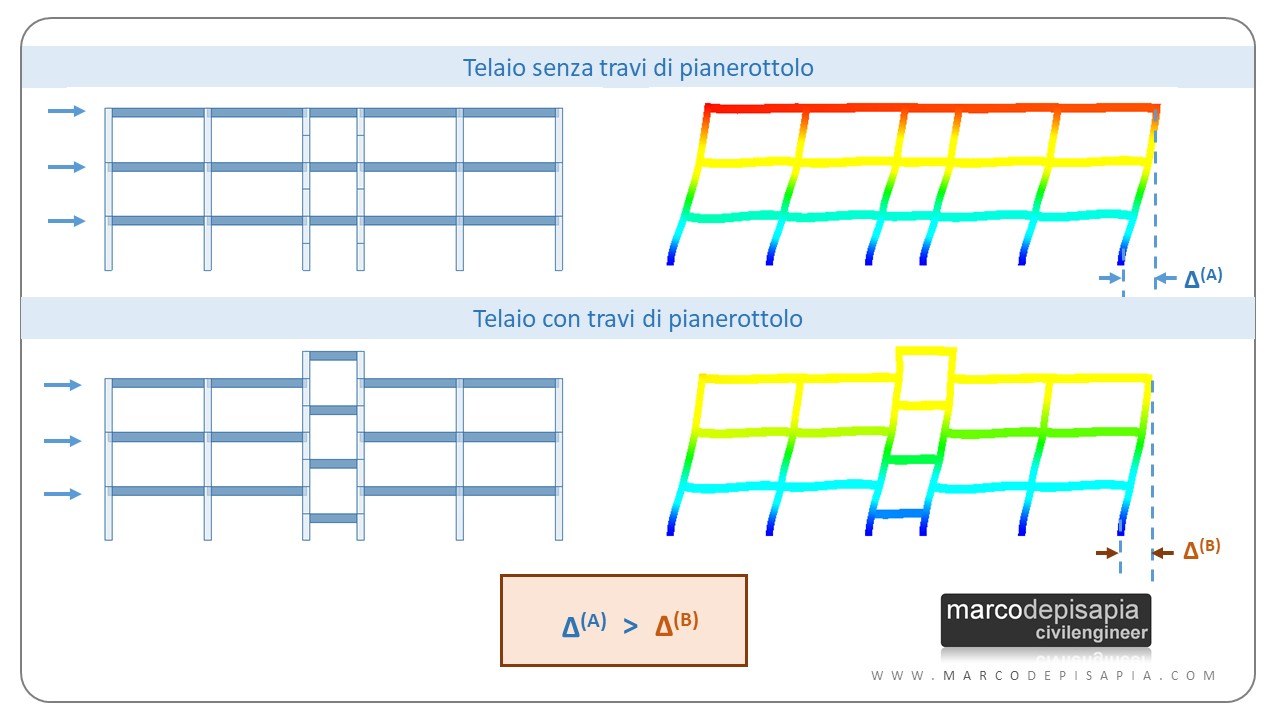
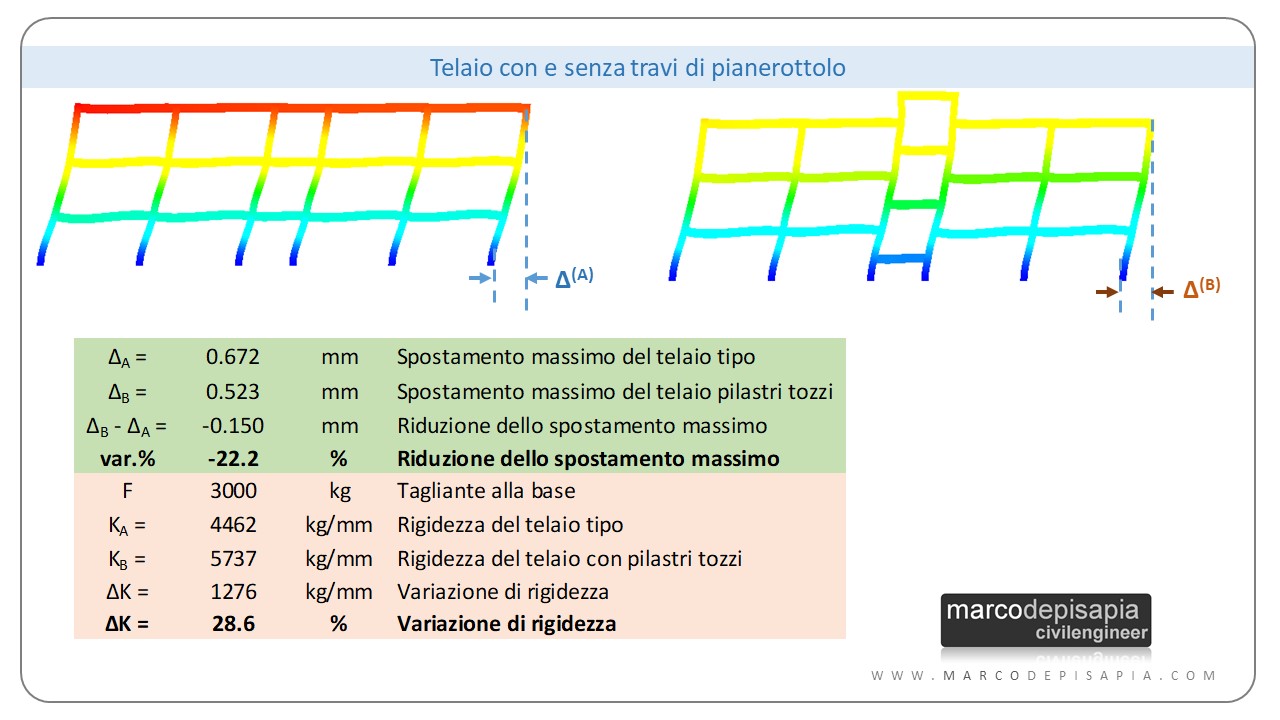
Per il telaio con le travi di pianerottolo gli spostamenti ottenuti si riducono di circa il 22% e la rigidezza aumenta del 28%, come puoi vedere dall’immagine seguente.

Scala in cemento armato: la migliore posizione in pianta (e le posizioni da evitare)

Da quanto detto finora, si può dedurre che la migliore posizione in pianta del corpo scala è una posizione quanto più baricentrica possibile, collocata su uno degli assi di simmetria della pianta dell’edificio. 

Un posizione eccentrica della scala, per esempio in uno spigolo della pianta rettangolare, crea una forte eccentricità fra il baricentro delle masse e delle rigidezze, come puoi vedere nell’immagine di seguito. 

In questa configurazione il primo modo di vibrare, che dovrebbe essere di traslazione lungo X, presenta una componente rotazionale con centro di rotazione coincidente con il corpo scala.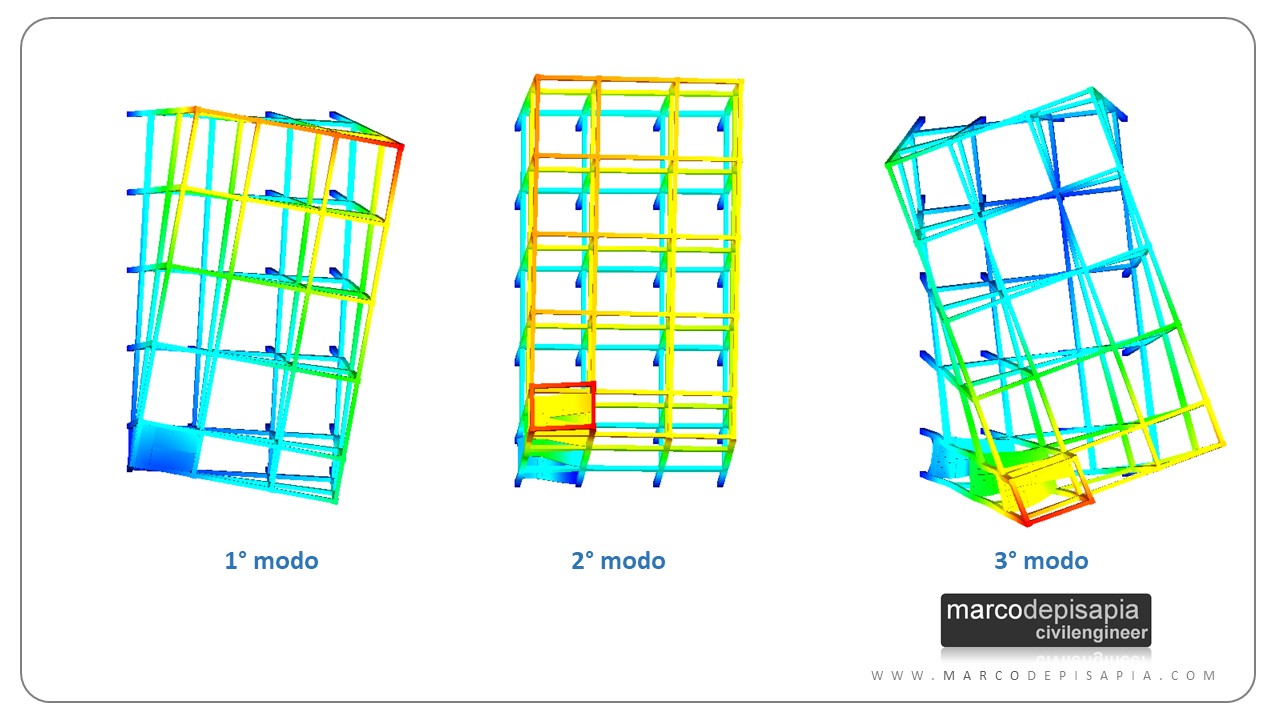

Nel caso in cui esigenze architettoniche non consentano una posizione baricentrica del corpo scala, bisognerà progettare la struttura di conseguenza, cercando di compensare l’eccentricità fra baricentro delle masse e delle rigidezze modificando l’orientamento in pianta del lato lungo dei pilastri (magari utilizzando il metodo ReC, te ne parlo in questo video), oppure in alternativa adottare il modello di scala alla Giliberti (ti spiego fra poco in cosa consiste).

Scala in cemento armato: il collegamento fra due impalcati successivi

Un altro elemento di irregolarità che la struttura del corpo scala comporta è il collegamento che crea fra gli impalcati. In assenza del corpo scala, i diversi impalcati sono collegati l’un l’altro esclusivamente tramite i pilastri. Pertanto lo spostamento relativo degli impalcati dipenderà dalla rigidezza flessionale e tagliante dei pilastri. 

In presenza del corpo scala, oltre alla rigidezza flessionale e tagliante dei pilastri, entra in gioco la rigidezza assiale delle solette delle rampe del corpo scala. Le solette del corpo scala sono elementi sub-orizzontali: il pianerottolo di riposo è orizzontale, le rampe hanno inclinazione solitamente inferiore a 30°. Pertanto gli spostamenti relativi fra due impalcati contigui chiamano in gioco le deformazioni assiali (oltre a quelle taglianti e flessionali) delle solette.

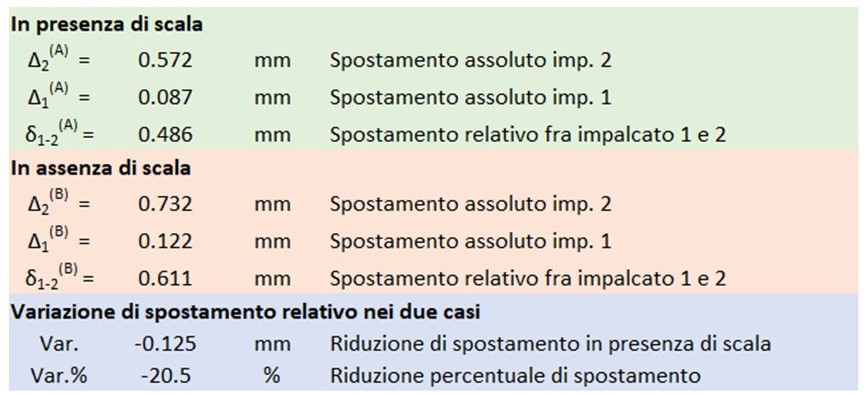
Nel’immagine seguente ti mostro gli spostamenti relativi fra l’impalcato 1 e 2 dello stesso modello analizzato in presenza e in assenza del corpo scala. Nei due casi ho caricato il modello con una distribuzione di forze orizzontali concentrate nei nodi, uguali e contrarie, al livello dell’impalcato 1 e 2, per valutare gli spostamenti relativi.

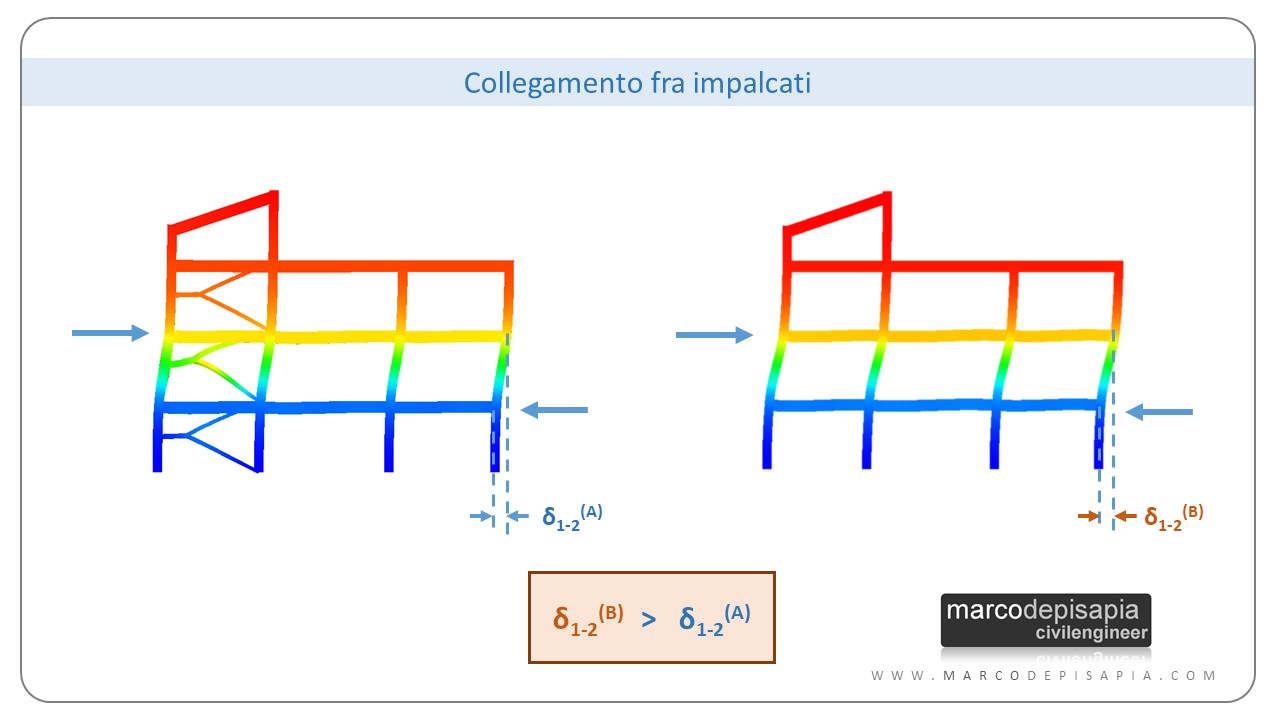
In presenza del corpo scala, lo spostamento relativo fra gli impalcati 1 e 2 si riduce del 20%.

Scala alla Giliberti: una soluzione alle irregolarità introdotte dal corpo scala

Una soluzione agli elementi di irregolarità introdotti dal corpo scala nelle strutture intelaiate fu proposta dall’ing. Aurelio Giliberti nel 1983. La sua proposta fu pubblicata nel numero 134/1983 della rivista “L’ingegnere Italiano“. 

L’obiettivo del modello di scala proposta dall’ing. Giliberti è quello di non alterare la regolarità del telaio spaziale a maglie ortogonali degli edifici in cemento armato. 

Prima di parlare dei vantaggi della scala alla Giliberti, vediamo innanzitutto le sue caratteristiche. Nella scala alla Giliberti i pianerottoli di riposo sono suddivisi in due parti indipendenti, una appartenente alla prima rampa, l’altra appartenente alla rampa di sbarco, separati  da un’idonea distanza reciproca (una sorta di giunto strutturale interno alla struttura).

Le travi di pianerottolo sono assenti, in tal modo si evita la creazione del pilastro tozzo. I pianerottoli della rampa in salita e della rampa in discesa sono collegati alla medesima trave di piano mediante dei pilastrini compressi nel primo caso e tesi nel secondo. Nell’immagine seguente puoi vedere delle immagini 3D estratte dal modello di calcolo che ho analizzato.

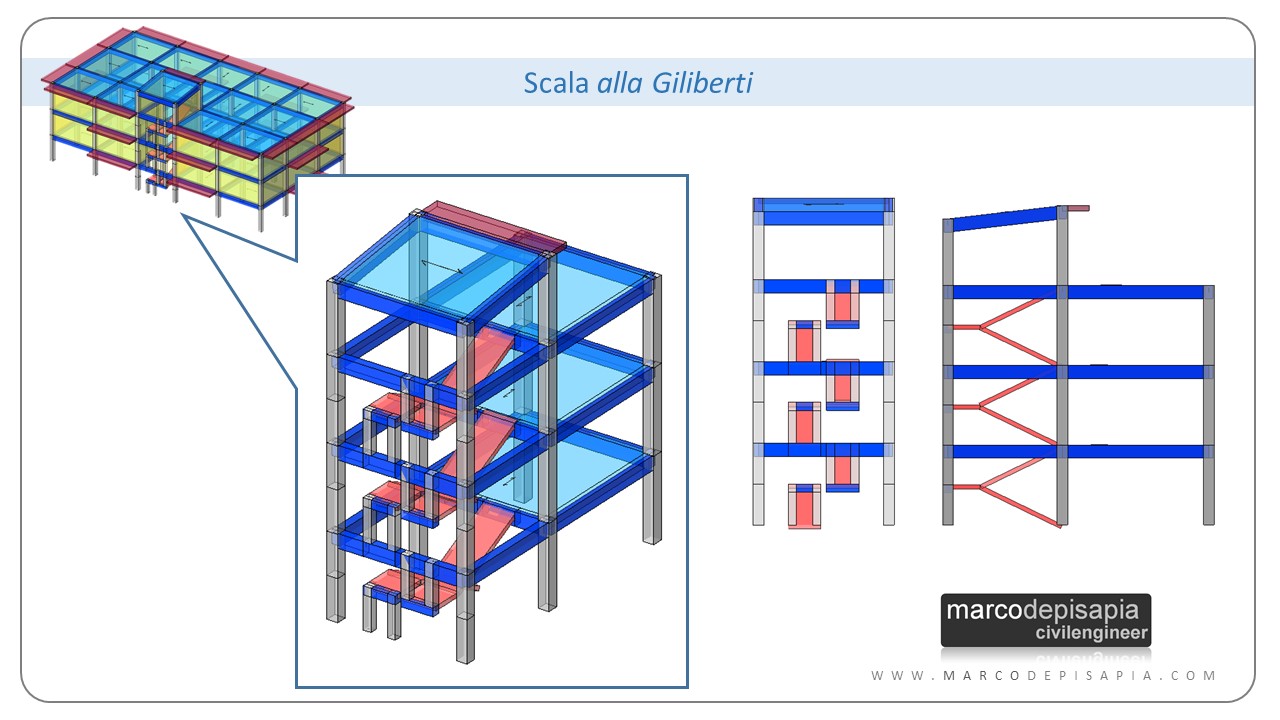
Nella scala alla Giliberti le rampe di salita e discesa appartengono ad un singolo impalcato, senza interferire in alcun modo con gli impalcati soprastante e sottostante e senza la necessità di una trave di pianerottolo per sostenere i pianerottoli di riposo.

Come puoi vedere dal’immagine seguente, caricando il primo e secondo impalcato con forze orizzontali concentrate nei nodi, uguali e contrarie, gli spostamenti relativi fra il primo e secondo impalcato non sono influenzati dalla presenza delle rampe della scala. Le due porzioni dei pianerottoli di riposo si spostano in verso opposto in maniera indipendente.

I vantaggi della scala alla Giliberti

I risultati che si ottengono realizzando una scala alla Giliberti sono i seguenti:

• assenza delle travi intermedie di pianerottolo e dei pilastri tozzi;
• nessuna modifica alla posizione del baricentro delle rigidezze;
• spostamenti relativi fra impalcati non alterati dalla presenza delle rampe della scala.

Nel modello di calcolo analizzato con scala alla Giliberti, il baricentro delle rigidezze coincide perfettamente con il baricentro delle masse (utilizzando pilastri di sezione quadrata e trascurando l’eccentricità accidentale del baricentro delle masse prescritta dalla Normativa).

I modi di vibrare sono disaccoppiati fra loro: il primo e il secondo modo sono puramente traslazionali in direzione X e Y. Il terzo modo è rotazionale attorno al baricentro delle rigidezze, la cui posizione non è stata modificata dalla presenza del corpo scala.

Scarica il Focus Analitico sulla scala alla Giliberti

La soluzione proposta dall’ing. Giliberti suscitò molta curiosità fra i tecnici del settore. Nel 1987, quattro anni dopo la prima pubblicazione del 1983, l’ing. Giliberti pubblicò un breve opuscolo di chiarimento, contenente una descrizione più dettagliata del suo modello di scala e alcuni esempi numerici.

Puoi scaricare l’opuscolo redatto dall’ing. Giliberti compilando i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download.

Nucleo scala con pareti in cemento armato: evita un errore frequente

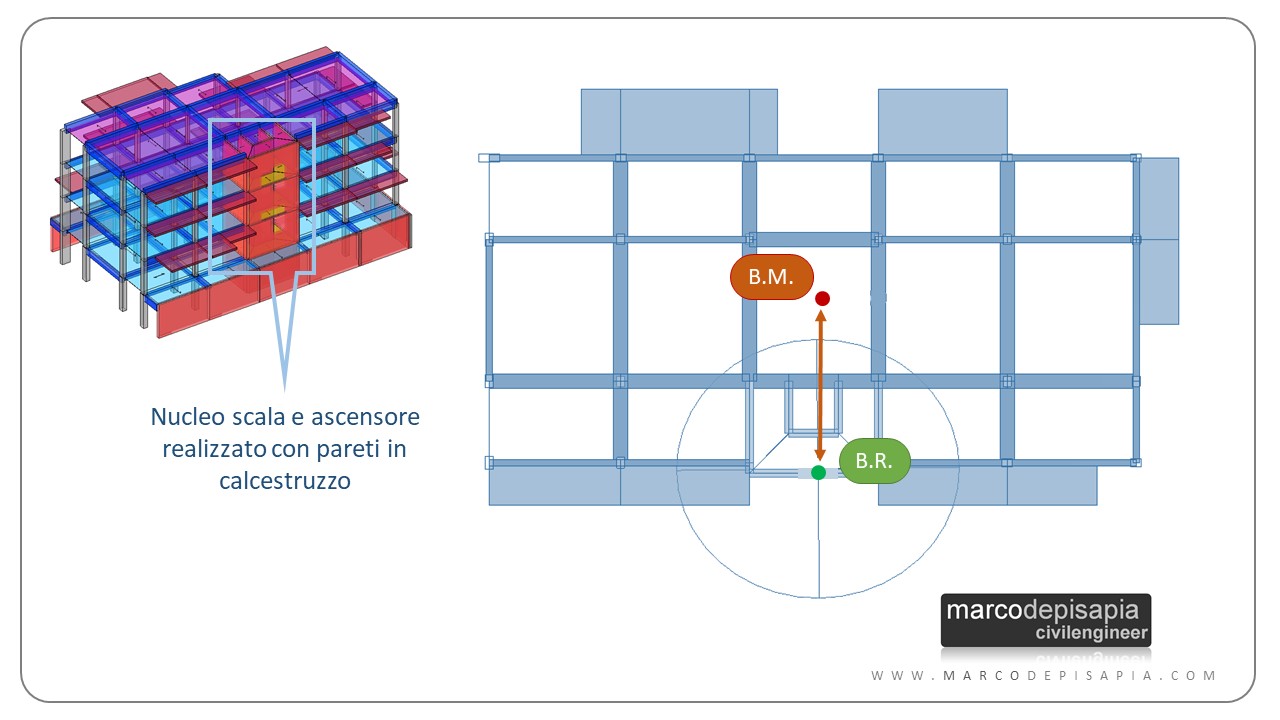
Dagli esempi visti finora dovrebbe esserti chiaro in che modo la struttura della scala alteri la regolarità delle strutture intelaiate. C’è un ultimo caso di cui vorrei parlarti: il nucleo scala e vano ascensore realizzato con pareti in calcestruzzo armato.

Se decidi di realizzare un nucleo scala realizzato con pareti in cemento armato, ti suggerisco di progettare l’intera struttura come struttura a pareti e non come struttura intelaiata.

Mi è capitato spesso di vedere un nucleo scala a pareti in una struttura intelaiata nei progetti per i quali mi è stata richiesta una consulenza tramite Calculation WEB, il servizio di calcolo strutturale dedicato esclusivamente ai professionisti del settore edile (trovi tutti i dettagli a questo link).

Inserire un nucleo scala realizzato con pareti in calcestruzzo armato in una struttura intelaiata crea un forte eccentricità fra baricentro delle masse e delle rigidezze. Il baricentro delle rigidezze risulterà posizionato sulla parete di lunghezza maggiore, in quanto molto più rigida rispetto ai pilastri.

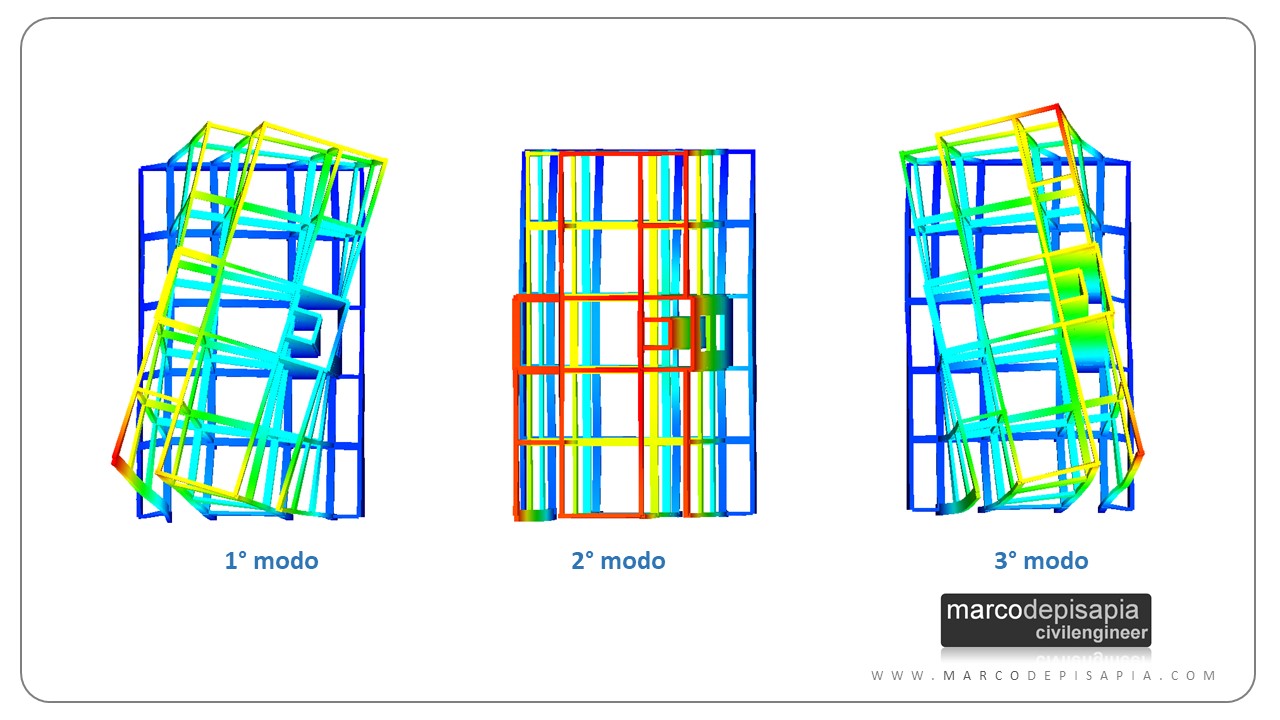
Anche i modi di vibrare della struttura ne risentiranno. Il primo modo di vibrare sarà rotazionale e il terzo modo, che in questo caso dovrebbe essere di traslazione lungo Y, sarà prevalentemente rotazionale, con centro di rotazione nel nucleo scale.

Conclusioni

La struttura del corpo scala negli edifici in calcestruzzo armato è un elemento critico che altera la regolarità delle maglie del telaio spaziale. Un corretto posizionamento in pianta della scala eviterà forti eccentricità fra il baricentro delle masse e delle rigidezza e i conseguenti effetti torsionali in presenza dell’azione sismica che aumenterebbero le sollecitazioni nei pilastri periferici. 

Il modello di scala alla Giliberti si rivela ancora oggi, a 40 anni dalla sua ideazione, attualissimo ed una valida soluzione per eliminare le irregolarità introdotte dalle scale in cemento armato. 

L’articolo di oggi finisce qui. Se l’hai trovato utile, puoi suggerirlo ai tuoi colleghi su Linkedin e ai tuoi amici su Facebook cliccando sui tasti di condivisione social in fondo alla pagina.

Al prossimo post.

Marco