Profilati in acciaio: come scegliere la giusta sezione dai sagomari (il caso pratico di un cancello)

In questo post ti mostro l’importanza della corretta scelta dei profilati in acciaio attraverso l’esposizione di un caso pratico riguardante la realizzazione di un cancello in acciaio. Alla fine dell’articolo potrai scaricare gratuitamente una raccolta di sagomari dei profilati in acciaio standard di uso più comune.

La scelta dei profilati in acciaio in fase di progettazione ha un’importanza fondamentale per il corretto comportamento statico di una costruzione. La scelta dei profilati in acciaio riguarda sia la forma della sezione trasversale (doppio T, U, L, tubolare etc.) che la dimensione della sezione a seconda del tipo di sollecitazione prevalente (compressione, flessione, torsione etc.) e dell’impegno statico dell’elemento strutturale.

Le sezioni trasversali dei profilati in acciaio rispettano delle dimensioni standard elencate in appositi sagomari, ovvero delle tabelle che riportano tutte le dimensioni della sezione e le principali proprietà geometriche come area, momento d’inerzia, modulo di resistenza, fattore di rigidezza torsionale e così via.

Profilati in acciaio: lo strano caso del cancello ballerino

Il caso pratico di cui ti parlo in quest’articolo per mostrarti l’importanza della corretta scelta dei profilati riguarda un cancello in acciaio che si comportava in modo strano all’apertura o alla chiusura.

Quando il cancello, azionato da un motore elettrico, iniziava a ruotare intorno all’asse verticale della sua cerniera, l’intera struttura metallica oscillava torsionalmente nel piano ortogonale al piano del cancello. Arrivato a fine corsa, l’oscillazione torsionale del cancello provocava un forte urto sul muro retrostante in fase di apertura o sul battente del controtelaio in fase di chiusura. Ti mostro di seguito un video dell’oscillazione torsionale esibita dal cancello.

Clicca su play per guardare il video del cancello

La struttura portante del cancello: i profilati in acciaio utilizzati

Hai visto il video precedente? Il comportamento insolito di questo cancello è dovuto alla scelta dei profilati in acciaio utilizzati per la realizzazione. La maglia strutturale del cancello è composta da tre profilati orizzontali HEA100 di lunghezza 3 metri e tre profilati verticali HEA100 di lunghezza 2.50 m.

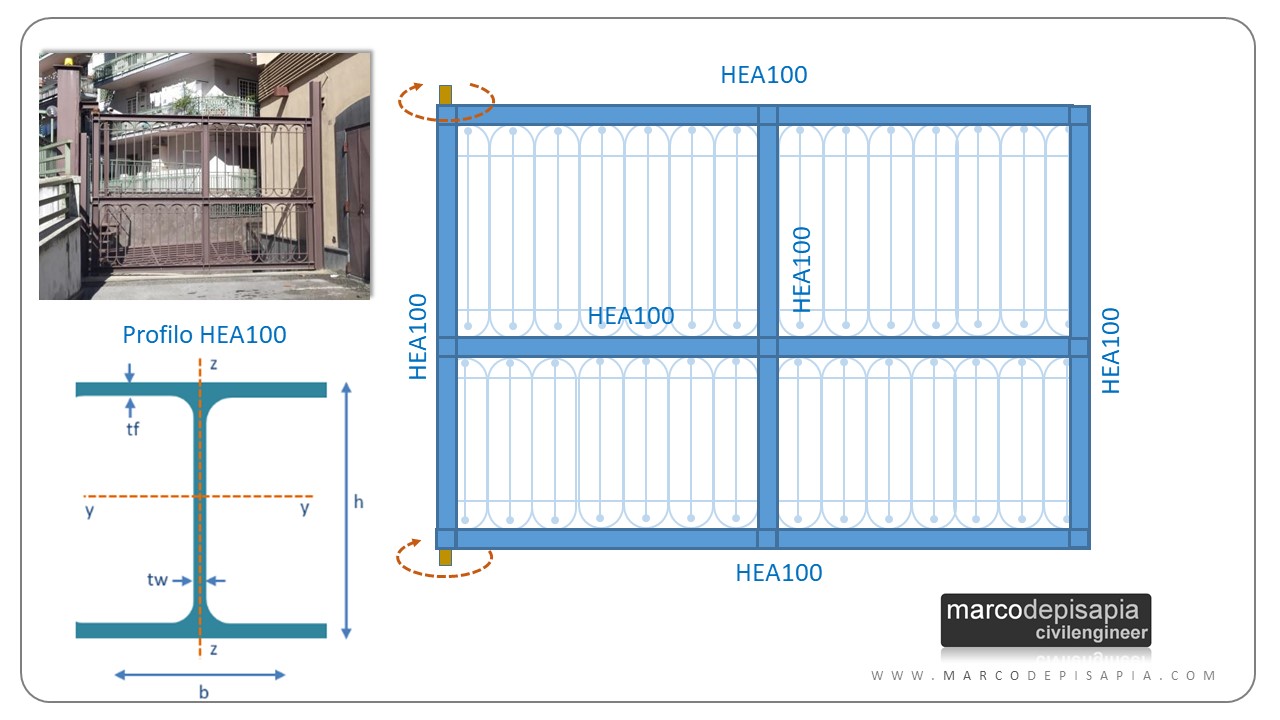
I profilati HEA sono caratterizzati da una sezione trasversale a doppio T. Questo tipo di profilati possiede un’elevata rigidezza flessionale intorno al’asse forte (asse y-y in figura), ma una bassa rigidezza torsionale e una bassa rigidezza flessionale intorno all’asse debole (asse z-z in figura). Inoltre questo tipo di profilo ha un peso considerevole di 16.7 kg/m che porta ad un peso totale della maglia strutturale del cancello di 275,5 kg.

L’origine delle oscillazioni torsionali

La bassa rigidezza torsionale del profilato centrale, accoppiata con la bassa rigidezza flessionale laterale dei profili all’estremità superiore e inferiore rendono il sistema molto flessibile, dando vita alle evidenti oscillazioni viste nel video. L’oscillazione viene innescata dall’accelerazione applicata alla struttura dal motore elettrico che lo aziona. Il braccio del motore elettrico, non perfettamente centrato rispetto al baricentro del cancello, dà vita all’oscillazione. Ti mostro un’immagine della deformazione che subisce il cancello durante un’oscillazione.

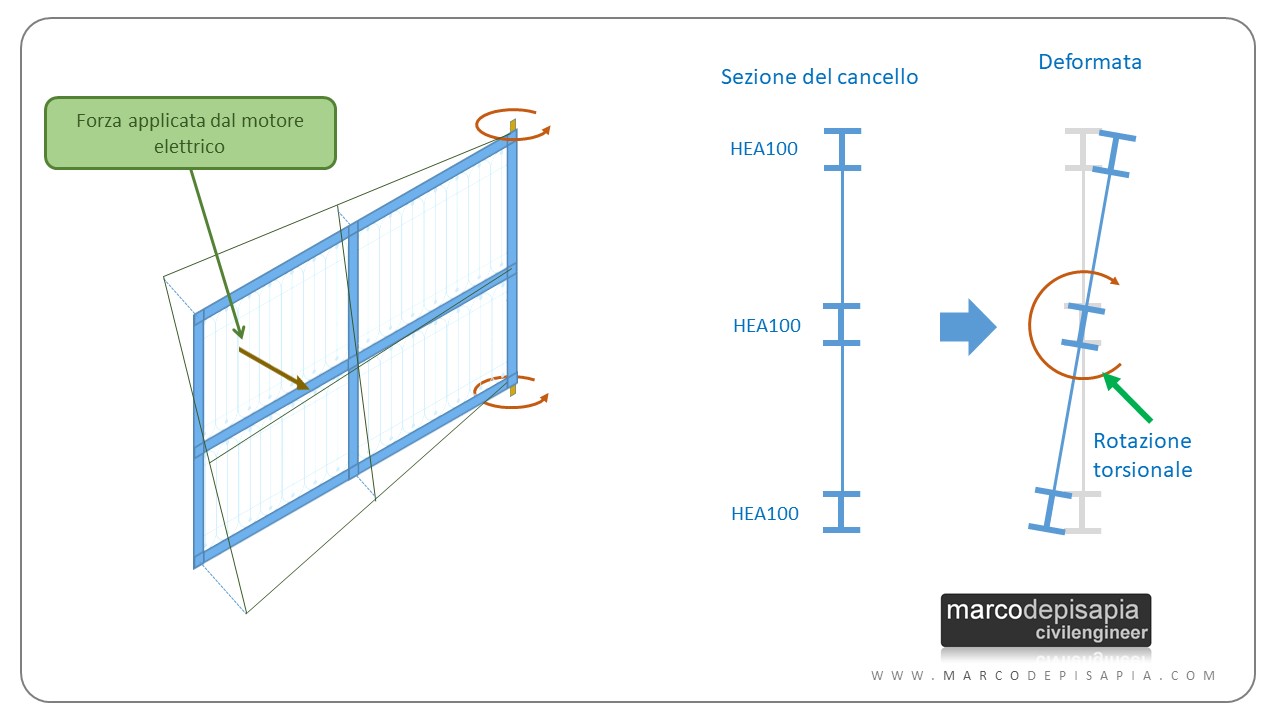
Rigidezza dei profilati in acciaio: l’influenza sul periodo di vibrazione

Trattandosi di un problema di oscillazioni, è possibile fare delle considerazioni sulle proprietà dinamiche del cancello. Ricordi la formula per il calcolo del periodo di vibrazione di un oscillatore semplice? Te la riporto di seguito:

T = 2 * π √( m / k)      “periodo di vibrazione di un oscillatore semplice”

• m = massa del sistema
• k = rigidezza del sistema

All’aumentare della massa e al diminuire della rigidezza aumenta il periodo di vibrazione del sistema. E’ proprio ciò che accade nel cancello in questione: elevata massa dovuta ai profili HEA e bassa rigidezza torsionale.

La formula che ti ho riportato sopra vale per un oscillatore semplice in cui le oscillazioni sono generata dalla traslazione di una massa nel piano. Le oscillazioni del cancello invece hanno a che fare con le rotazioni. In questo caso la formula del periodo di vibrazione è leggermente diversa:

T = 2 * π √( I / k_T)

• I = momento d’inerzia del sistema rispetto all’asse di rotazione;
• k_T = rigidezza torsionale del sistema.

La formula che ti ho riportato sopra si adatta proprio al nostro caso specifico. Il momento d’inerzia del sistema calcolato attorno all’asse del profilo centrale è elevato a causa del peso considerevole dei due profili di estremità. La rigidezza torsionale del sistema è bassa, a causa della bassa rigidezza torsionale del profilo centrale accoppiata alla basse rigidezza flessionale laterale e torsionale dei profili di estremità. Il risultato è un periodo di vibrazione elevato. 

Veniamo al punto chiave di questo post. Come si risolve il problema? Al proprietario del cancello non interesserà nulla di momenti d’inerzia e rigidezze torsionali. Vorrà soltanto una soluzione che gli permetta di avere un cancello che funzioni normalmente. Ti riporto di seguito la soluzione che è stata adottata per risolvere il problema. Continua a leggere.

Dalla teoria alla pratica: come risolvere il problema del cancello ballerino

Non è sempre necessario conoscere complesse nozioni teoriche per risolvere un problema di statica o dinamica come in questo caso. Nel caso specifico la soluzione al problema è stata trovata da un fabbro di navigata esperienza, interpellato per risolvere il problema in questione. Il fabbro, pur non sapendo nulla di rigidezze torsionali, oscillatori semplici e periodi di vibrazione, ha proposto una soluzione semplice, pratica ed economica.

Per eliminare il problema ha deciso di saldare una piastrina rettangolare in acciaio di spessore 5 mm alle estremità delle ali dei profilati orizzontali e verticali, per tutta la lunghezza e altezza del cancello. La piastra è stata saldata sui tre profili orizzontali e sui tre verticali solo dal lato interno del cancello per non appesantirlo troppo. In tal modo la sezione dei profilati è passata da una sezione a doppio T ad una sezione tubolare con due ali su un lato. Thats’it! Problema risolto. Magicamente le oscillazioni del cancello sono scomparse.

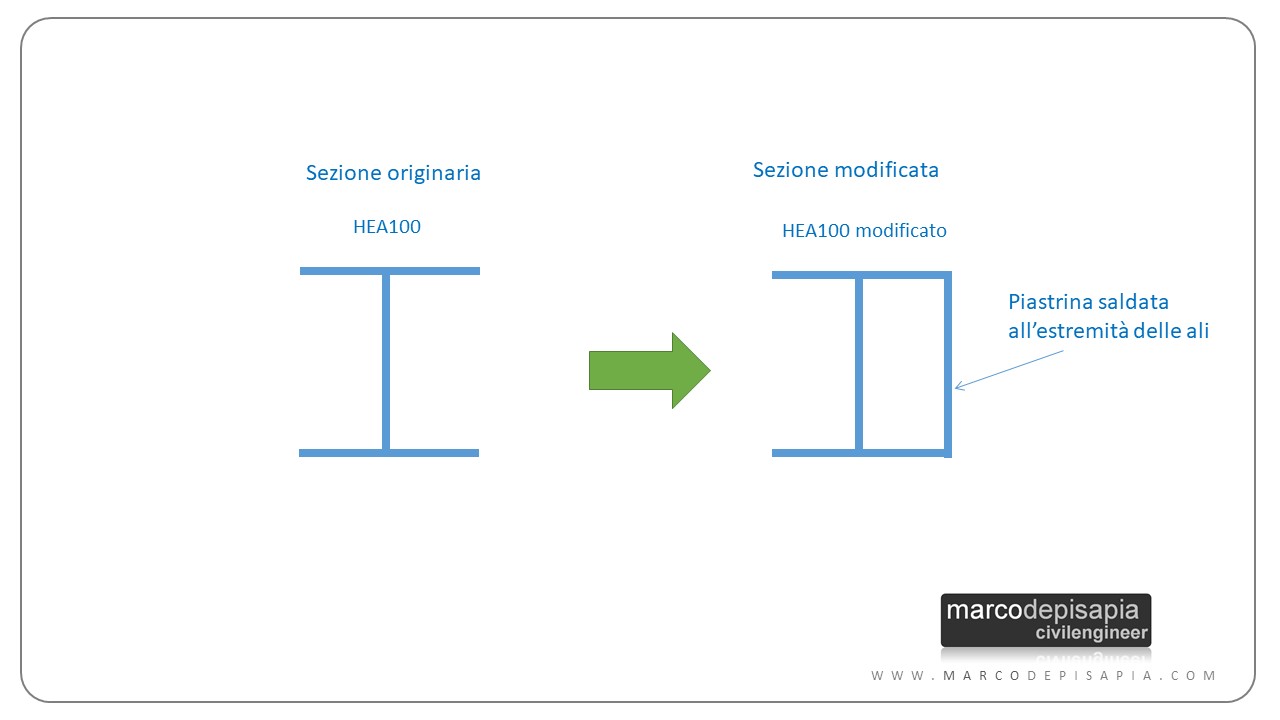
La modifica della sezione dei profilati in acciaio: perché la soluzione funziona?

Il ragionamento del fabbro, frutto della sua esperienza, è stato il seguente:

I profili a doppio T si usano per i solai, non per i cancelli. Per i cancelli si usano i profili tubolari. Se saldo una piastrina lungo il lato del profilo, trasformo un profilo ad I in un profilo tubolare.

Giovanni il fabbro

I profili tubolari hanno una rigidezza torsionale molto più elevata dei profili sottili a sezione aperta come per esempio i profili a doppio T (ti ho mostrato un confronto alla fine di quest’articolo). Aumentando la rigidezza torsionale del sistema, diminuirà il periodo di vibrazione e le oscillazioni scompariranno.

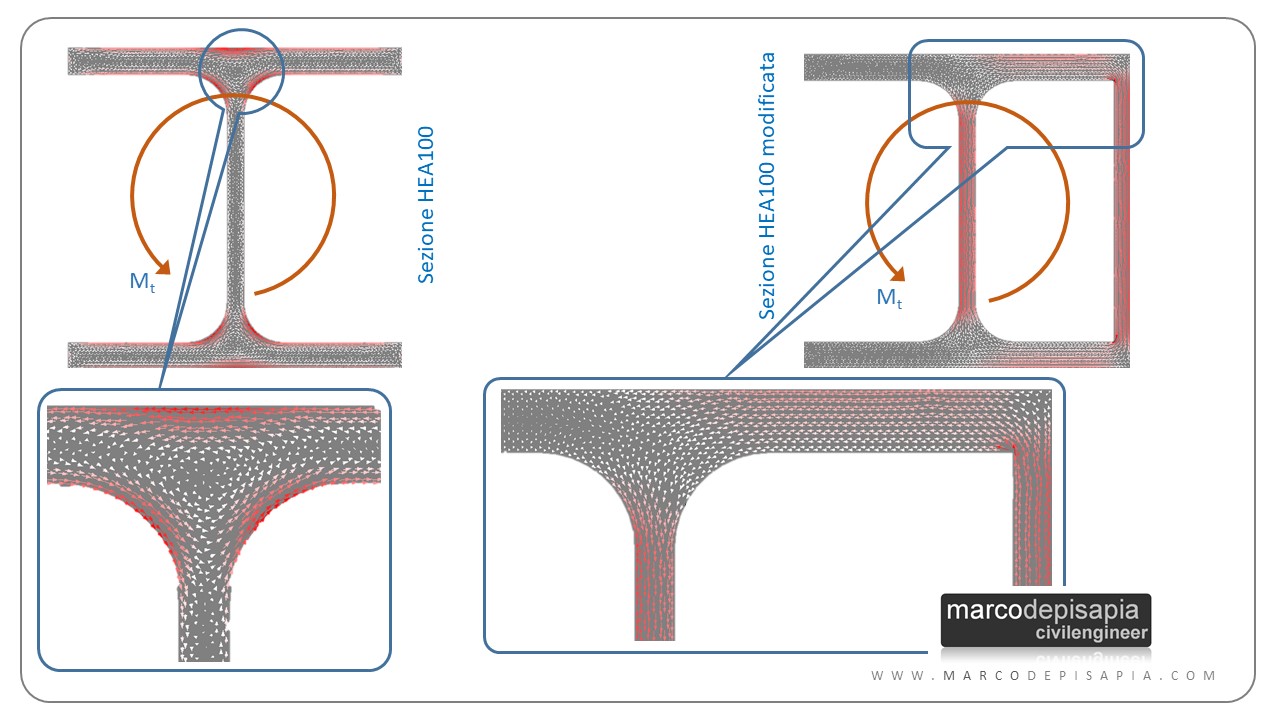
L’elevata rigidezza torsionale dei profilati tubolari è dovuta alla loro forma e alla distribuzione delle tensioni tangenziali da torsione che ne derivano. La forma chiusa del profilo genera un flusso di tensioni tangenziali che segue la forma del profilo. Nella sezione a doppio T invece il flusso delle tensioni ha un andamento diverso. Le tensioni che circuitano in verso opposto lungo la sezione del profilo sono molto ravvicinate, il valore di queste tensioni sarà molto elevato. Di conseguenza si avranno alte deformazioni del profilo.

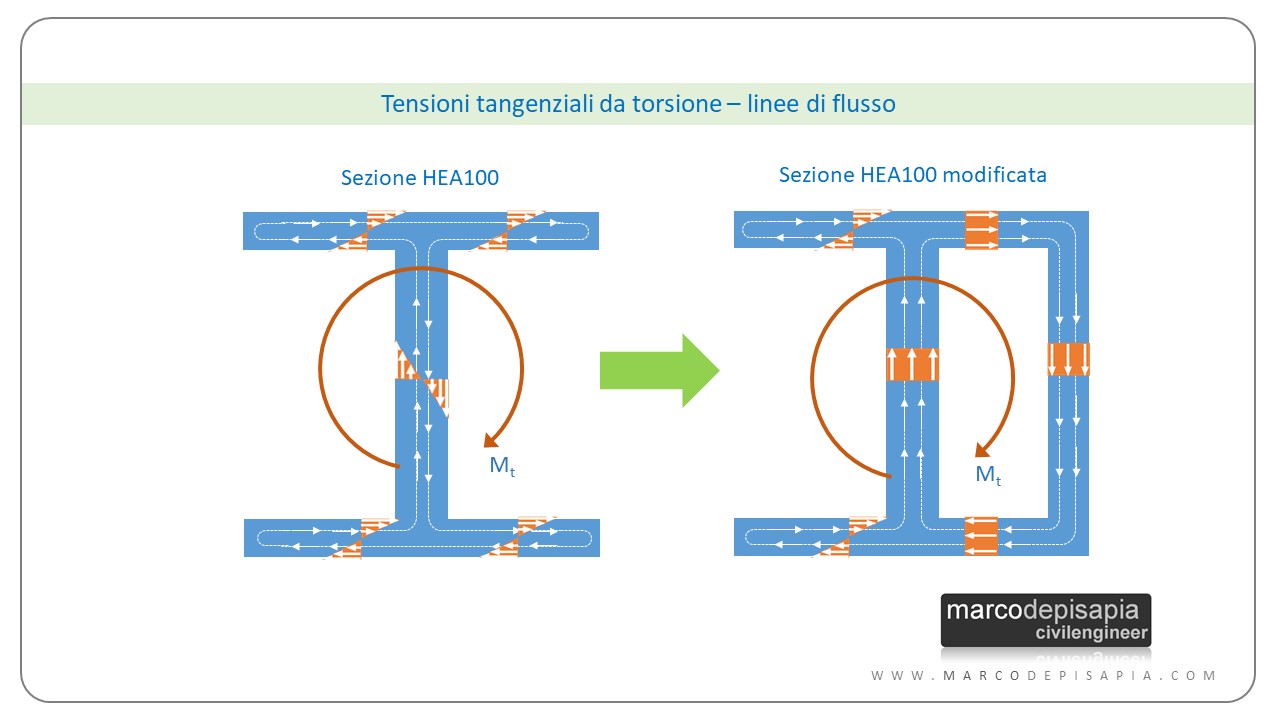
Rigidezza torsionale: confronto numerico fra le due sezioni

Proviamo a supportare quanto detto finora con qualche valutazione numerica. Ti riporto di seguito il fattore di rigidezza torsionale Jt della sezione a doppio T e della sezione modificata con l’aggiunta della piastrina su un lato. I dati sono stati ottenuti utilizzando un tool per l’analisi delle sezioni.

• profilo HEA100: fattore di rigidezza torsionale Jt =  5.23 cm⁴
• profilo HEA100 modificato: fattore di rigidezza torsionale Jt =  168.76 cm⁴

Come puoi vedere il fattore di rigidezza torsionale del profilo modificato è circa trenta volte maggiore del fattore di rigidezza torsionale del profilo HEA100. Ciò vuol dire che il profilo così modificato sarà trenta volte più rigido del profilo HEA100 originario.

Profilati in acciaio: scarica il sagomario PDF

Ho raccolto in un unico documento PDF i sagomari in formato tabellare delle sezioni in acciaio di uso più comune. Potrai utilizzare il sagomario PDF per progettare o verificare sezioni in acciaio. Scaricalo al link seguente:

Scarica Ver.Steel, l’app per il progetto e verifica di sezioni in acciaio

Per eseguire in maniera automatica il progetto e verifica delle sezioni in acciaio puoi scaricare gratuitamente Ver.Steel, l’app per l’analisi delle sezioni in acciaio. Compila i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download dell’applicazione.

Conclusioni

Siamo partiti dall’esempio pratico di un cancello, passando per le rigidezze torsionali dei profilati e per i periodi di vibrazione di un oscillatore semplice, fino ad un fabbro che risolve problemi. Ciò che devi ricordare di questo post è che la scelta dei profilati in acciaio va eseguita con consapevolezza in funzione della sollecitazione prevalente che sollecita un elemento strutturale. Ti riporto di seguito alcuni consigli sulle sezioni dei profilati da utilizzare a seconda dei casi:

• sezioni a doppio T: da preferire per sollecitazioni prevalenti di flessione (travi IPE) o pressoflessione (colonne HEA, HEB, HEM);
• sezioni tubolari: ideali per sollecitazioni prevalenti torsionali, si adattano bene anche per flessione, pressoflessione e compressione;
• angolari e UPN: peferibili per assorbire sollecitazioni di compressione, in quanto dotati di bassa resistenza flessionale e torsionale.

Questo post finisce qui. Se l’articolo ti è piaciuto puoi suggerirlo ai tuoi colleghi su Linkedin o ai tuoi amici su Facebook cliccando sui tasti di condivisione social in fondo alla pagina. E tu come avresti risolto il problema del cancello ballerino? Puoi farmelo sapere lasciando un commento al post.

Al prossimo articolo.

Marco

Aggiornato il 9/3/2020, pubblicato il 28/11/2016.