L’instabilità delle aste snelle provocata dall’applicazione di un carico di punta è un tema di fondamentale importanza per la progettazione e verifica strutturale di costruzioni in acciaio. In quest’articolo ti mostro:
- cos’è l’instabilità per carico di punta;
- cos’è il carico critico euleriano e come si calcola;
- cos’è la snellezza dell’asta e perché è così importante per valutare il carico critico euleriano.
Nel corso dell’articolo potrai scaricare un’utile applicazione per l’esecuzione della verifica di stabilità a compressione delle aste in acciaio, un Focus Analitico PDF che illustra il procedimento analitico per il calcolo del carico critico euleriano e una risorsa utility per la simulazione interattiva del fenomeno dell’instabilità per carico di punta. Non perderti le risorse allegate all’articolo.

In fase di progettazione bisogna tenere in seria considerazione l’effetto del carico di punta, in particolar modo per le strutture in acciaio, i cui elementi, per l’elevata resistenza del materiale, sono caratterizzati da sezioni ridotte ed elevata snellezza.
Scarica l’app Ver.Steel (xls di Microsoft Excel) per il progetto e verifica di sezioni in acciaio

Ver.Steel è l’app per il progetto e verifica di stabilità di aste in acciaio sottoposte a carico di punta implementata in Microsoft Excel. Puoi scaricare la versione gratuita dell’app compilando i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download.

Instabilità per carico di punta: l’esperimento dello spaghetto
L’instabilità per carico di punta si verifica quando un’asta snella, sottoposta ad un carico di compressione, manifesta un’inflessione laterale. Teoricamente un’asta sollecitata dal solo sforzo normale dovrebbe presentare soltanto deformazioni assiali senza inflettersi.
Nella realtà l’effetto combinato della snellezza dell’asta e delle imperfezioni iniziali (aste non perfettamente rettilinee) producono l’inflessione laterale per carico di punta. In corrispondenza del carico critico di stabilità l’asta presenterà due configurazioni di equilibrio: una configurazione indeformata (asta rettilinea) e una configurazione deformata (asta inflessa).
Per comprendere il fenomeno dell’instabilità di punta ti mostro un esperimento che puoi facilmente riprodurre utilizzando uno spaghetto. Uno spaghetto si presta molto bene per la riproduzione del fenomeno dell’instabilità per due motivi:
- non è mai perfettamente rettilineo, proprio come non lo sono gli elementi strutturali nella realtà;
- puoi facilmente spezzarlo in più parti per riprodurre aste di diversa lunghezza e di conseguenza di diversa snellezza.
Instabilità per carico di punta: come eseguire l’esperimento dello spaghetto
Prendi due spaghetti, lasciane uno intero, spezza l’altro a metà e spezza ancora a metà una delle due parti ottenute. Avrai quindi tre spaghetti dalle seguenti lunghezze:
- uno spaghetto lungo un quarto di quello intero;
- uno spaghetto lungo la metà di quello intero;
- uno spaghetto intero.
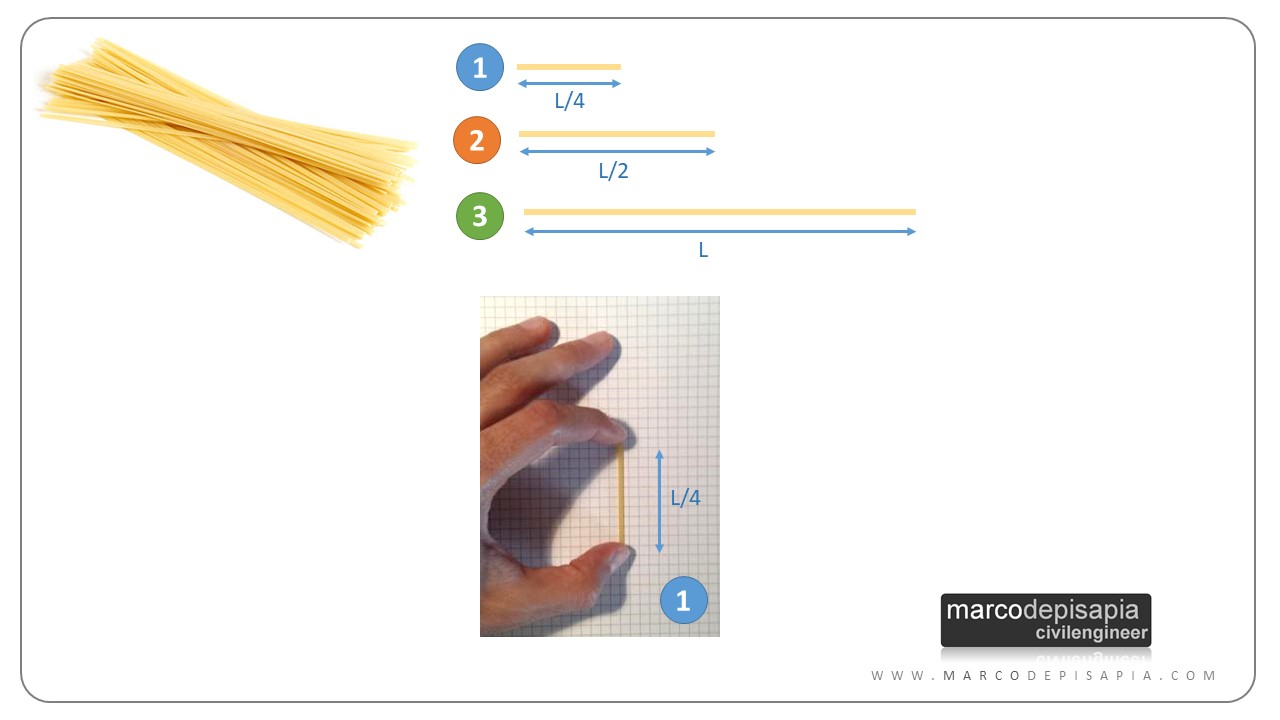
Prendi lo spaghetto lungo un quarto e comprimilo fra due dita. Lo spaghetto resisterà molto bene alla compressione. Anche applicando un’elevata pressione con le dita, lo spaghetto resterà perfettamente rettilineo.
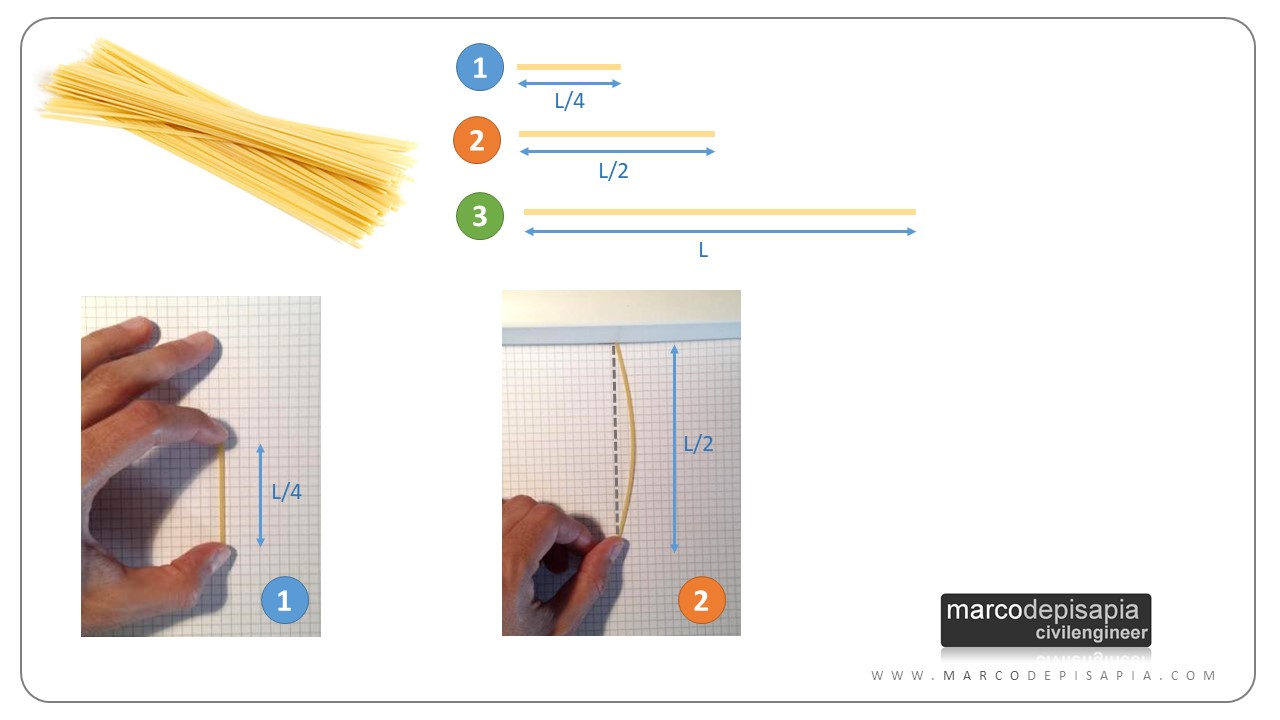
Prendi la spaghetto lungo la metà e comprimilo allo stesso modo di quello precedente. Questa volta aumentando la pressione alle estremità dello spaghetto potrai vederlo inflettersi leggermente.
Fai infine la stessa cosa con l’ultimo spaghetto, quello di lunghezza intera. Stavolta lo spaghetto si infletterà lateralmente per una pressione molto più bassa rispetto al caso visto prima. Con molta probabilità riuscirai anche a spezzare lo spaghetto, applicando una pressione molto inferiore rispetto a quella applicata sul precedente spaghetto.

Prova anche tu ad eseguire l’esperimento dello spaghetto, in poco tempo ti renderai conto del fenomeno dell’instabilità per carico di punta.
Instabilità per carico di punta: cosa possiamo dedurre da quest’esperimento?
La differenza fra i tre spaghetti dell’esperimento sta soltanto nella loro lunghezza. Il materiale di cui sono composti è sempre lo stesso. Lo spaghetto di lunghezza intera sopporta una pressione minore non perché il materiale di cui è composto (la pasta in questo caso) raggiunge la massima tensione resistente, ma perché si infletterà e non sarà in grado di resistere a sforzi di compressione maggiori.
All’aumentare della lunghezza dello spaghetto, aumenterà la snellezza e diminuirà la capacità di resistere a sforzi di compressione. Vedremo tra poco come si definisce la snellezza di un’asta. Continua a leggere.
Il carico critico euleriano
Il comportamento delle aste sottoposte al carico di punta fu studiato analiticamente per la prima volta dal matematico svizzero Leonhard Eulero intorno alla metà del 1700.
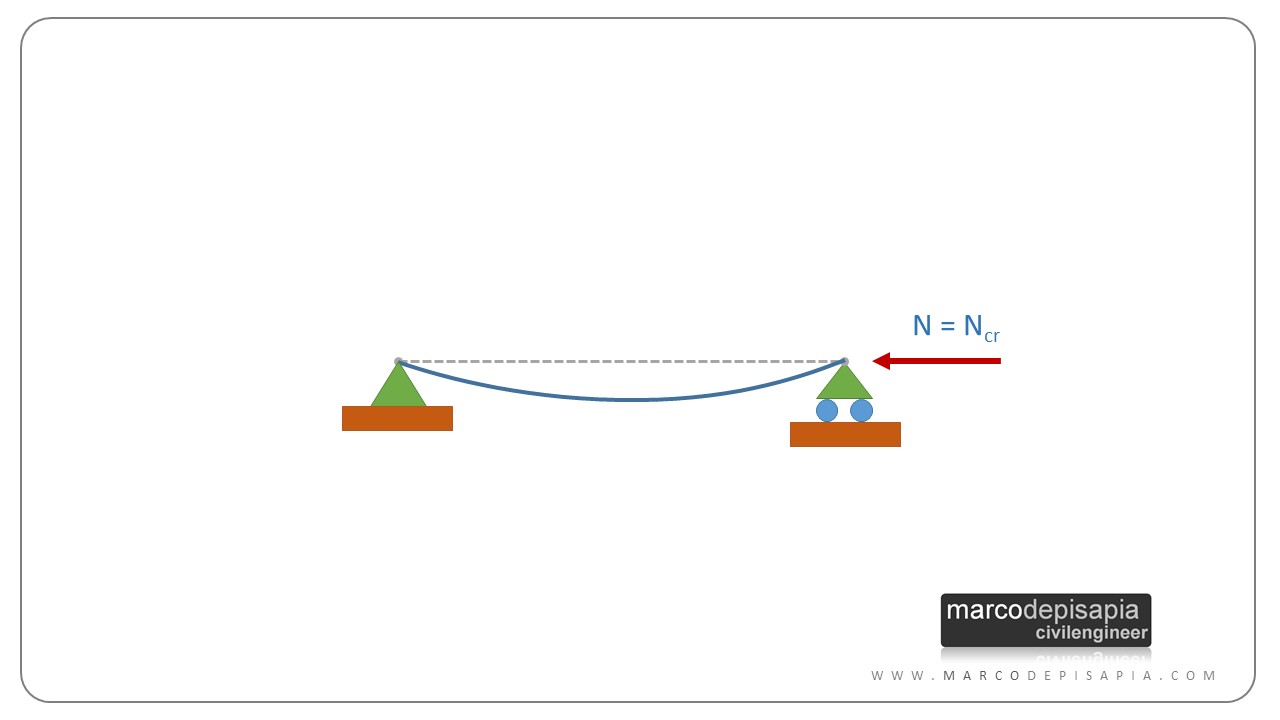
Eulero ottenne un formula per il calcolo del carico critico che mette in relazione la snellezza di un’asta con la tensione di compressione che l’asta è in grado di sopportare. Ti riporto di seguito la formula del carico critico euleriano.
Ncr = π2 E Imin / L02
- Imin = momento d’inerzia minimo della sezione;
- E = modulo elastico del materiale;
- L0 = lunghezza di libera inflessione dell’asta.
Formula del carico critico euleriano
Sostituendo il rapporto Imin / L02 = A (ρmin2 / L02) = A/λmax2 in cui
- λmax = snellezza massima dell’asta = L0/ρmin
- ρmin = raggio d’inerzia minimo della sezione
si ottiene la formula del carico critico euleriano in funzione della snellezza dell’asta:
Ncr = π2 E A / λmax2
- A = area della sezione;
- E = modulo elastico del materiale;
- λmax = snellezza massima dell’asta rispetto all’asse y e z;
Formula del carico critico euleriano in funzione della snellezza
Scarica il Focus Analitico PDF sul calcolo del carico critico euleriano

La formula del carico critico di stabilità euleriana è stata ottenuta eseguendo un’analisi del secondo ordine, ovvero un’analisi che considera l’equilibrio del sistema strutturale tenendo conto della sua configurazione deformata e portando in conto le non linearità geometriche. Trovi il procedimento analitico per il calcolo del carico critico euleriano nel Focus Analitico PDF scaricabile gratuitamente. All’interno troverai anche le prescrizioni delle NTC2018 per l’esecuzione della verifica di stabilità per carico di punta per le aste in acciaio. Clicca sul bottone qui sotto per scaricare il Focus Analitico PDF.

La curva di stabilità euleriana
E’ possibile rappresentare la tensione critica σcrit, ottenuta dal rapporto fra il carico critico euleriano e l’area della sezione, in un grafico cartesiano in funzione della snellezza. All’aumentare della snellezza, diminuirà la resistenza a compressione. Nel punto in cui la tensione σcrit uguaglia la tensione resistente di compressione dell’acciaio, si avrà la snellezza critica. Per valori della snellezza minori della snellezza critica, l’asta si dirà tozza. Per valori della snellezza maggiore della snellezza critica l’asta sarà snella.
Nell’immagine sottostante puoi vedere la curva di stabilità euleriana e le configurazioni deformate dei tre spaghetti dell’esperimento. Per ciascuno di essi è stata evidenziata la zona della curva di stabilità euleriana alla quale appartengono.
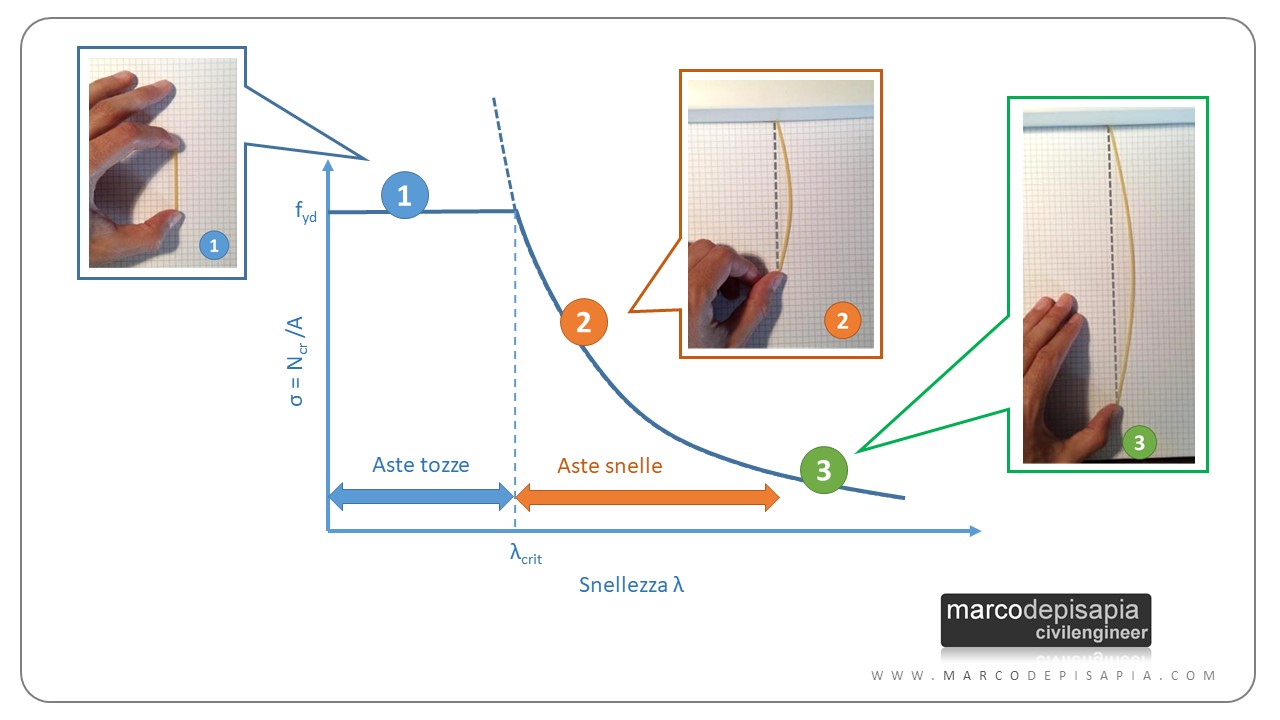
Snellezza dell’asta e lunghezza di libera inflessione
Come hai potuto vedere dalla formula del carico critico euleriano, lo sforzo di compressione che genera inflessione laterale dipende dalla snellezza. Per ottenere lo sforzo di compressione critico minimo, bisognerà inserire nella formula il valore massimo della snellezza. Ciascuna asta compressa sarà dotato di due valori della snellezza:
λy = snellezza per sbandamento intorno all’asse y;
λz = snellezza per sbandamento intorno all’asse z.
Per il calcolo del carico critico euleriano bisognerà utilizzare la snellezza massima all’interno della formula:
λmax = max( λy = L0,y / ρy ; λz = L0,z / ρz)
- L0,y = lunghezza di libera inflessione per sbandamento intorno all’asse y;
- L0,z = lunghezza di libera inflessione per sbandamento intorno all’asse z;
- ρy = √(Iy/A) = raggio d’inerzia rispetto all’asse y;
- ρz = √(Iz/A) = raggio d’inerzia rispetto all’asse z.
La Normativa Tecnica prescrive di limitare la snellezza delle aste compresse al valore di 200 per le membrature principali e 250 per le membrature secondarie.
La lunghezza di libera inflessione è pari alla distanza fra due punti di flesso della configurazione deformata e dipende dalle condizioni di vincolo all’estremità dell’asta. A ciascuna condizione di vincolo dell’asta corrisponderà un coefficiente β per il calcolo della lunghezza di libera inflessione.
L0,y = βy ⋅ L
L0,z = βz ⋅ L
- βy = coefficiente di vincolo per inflessione intorno all’asse y;
- βz = coefficiente di vincolo per inflessione intorno all’asse z;
Lunghezza di libera inflessione dell’asta compressa
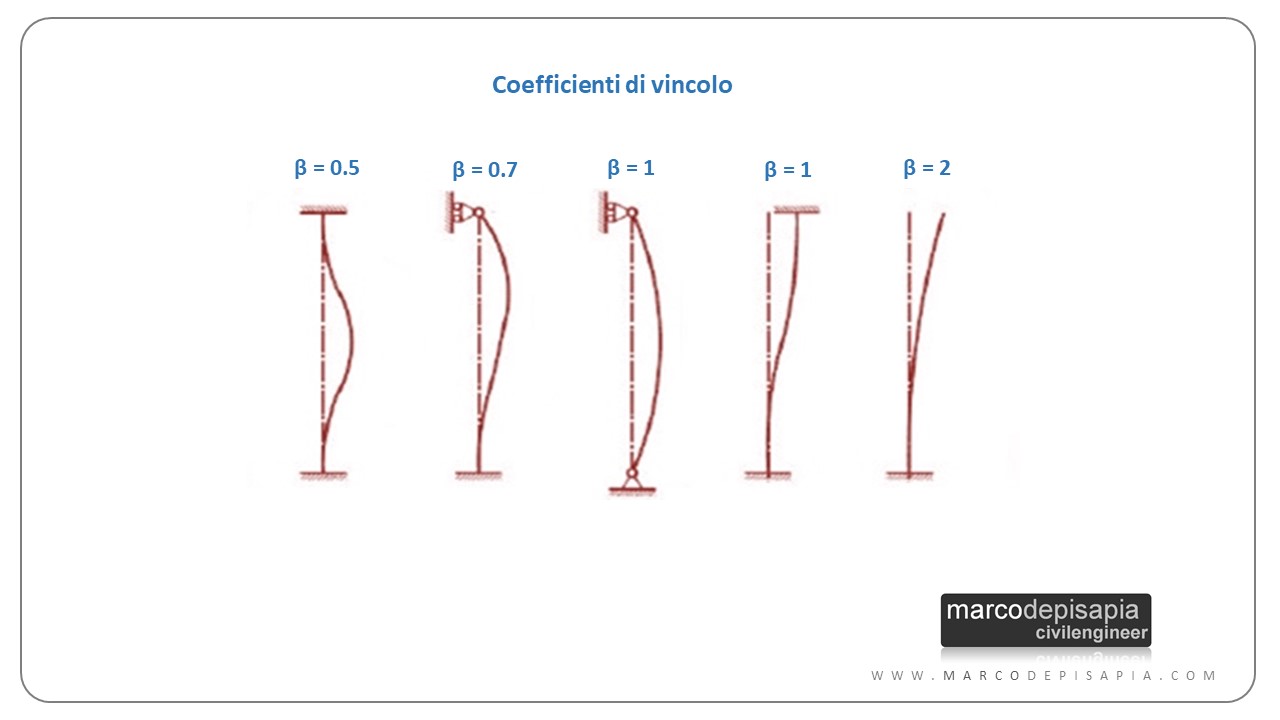
Ti riporto di seguito i valori del coefficiente β per le più comuni condizioni di vincolo:
- incastro – incastro → β = 0.5
- incastro – appoggio → β =0.7
- appoggio – appoggio → β = 1
- mensola → β = 2
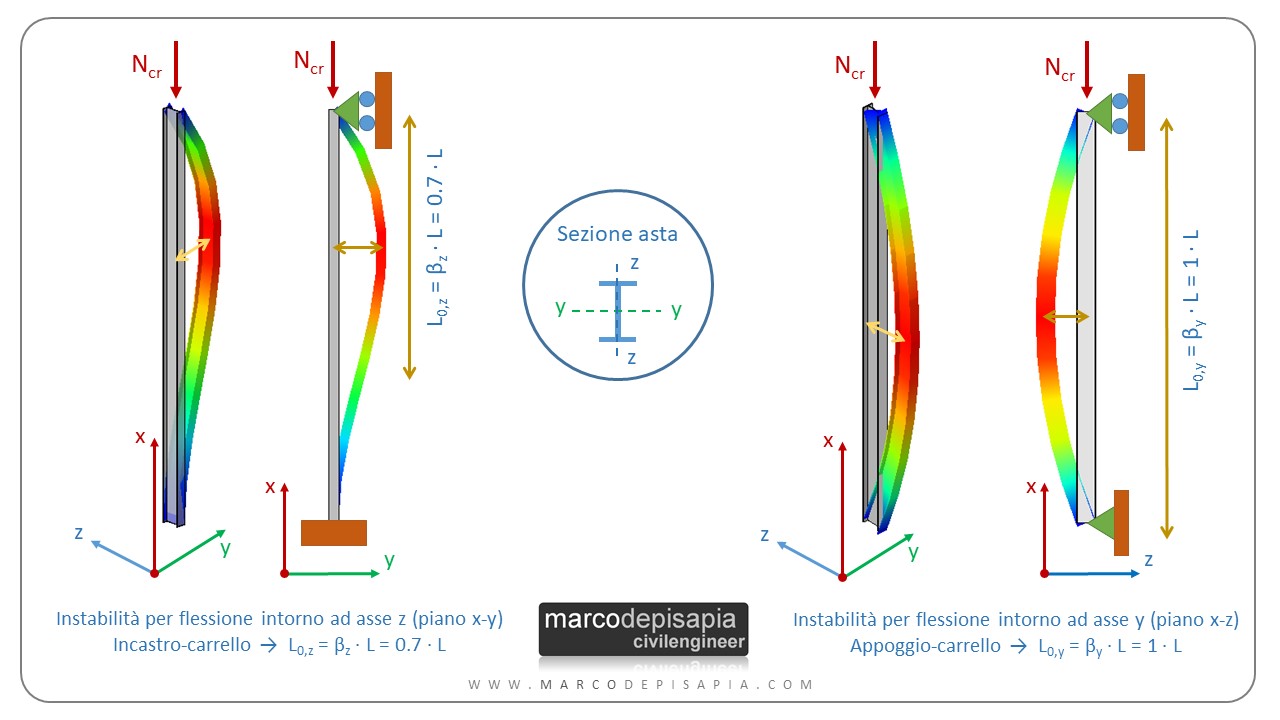
La lunghezza di libera inflessione può essere diversa nel piano x-z e nel piano x-y perché potrebbero essere diverse le condizioni vincolari in questi due piani. Ti riporto un esempio nell’immagine seguente in cui l’asta è incastrata-appoggiata nel piano x-y e appoggiata-appoggiata nel piano x-z.
Carico di punta: le curve di stabilità della Normativa Tecnica
La curva di stabilità euleriana descrive il comportamento ideale dell’asta strutturale ed è stata ottenuta attraverso una modellazione matematica del fenomeno.
Il comportamento di un asta reale differisce leggermente dall’asta di Eulero. Per ottenere le curve di stabilità di aste reali i laboratori sperimentali di strutture hanno eseguito prove di resistenza a compressione su aste in acciaio di diverse classi di resistenza, diverse tipologie di sezione e di diversa lunghezza. A ciascuna lunghezza corrisponde una snellezza e un diverso valore del carico di instabilità. Riportando in un piano cartesiano i risultati sperimentali della resistenza a compressione in funzione della snellezza per ogni tipologia di sezione e di classe di resistenza, sono state ottenute cinque differenti curve di stabilità, denominate a0, a, b, c, d, da utilizzare nella verifica strutturale di aste compresse in acciaio.
Nell’immagine sotto, insieme con la curva di stabilità euleriana ho rappresentato le cinque curve sperimentali di stabilità proposte dalla Normativa Tecnica NTC2018.
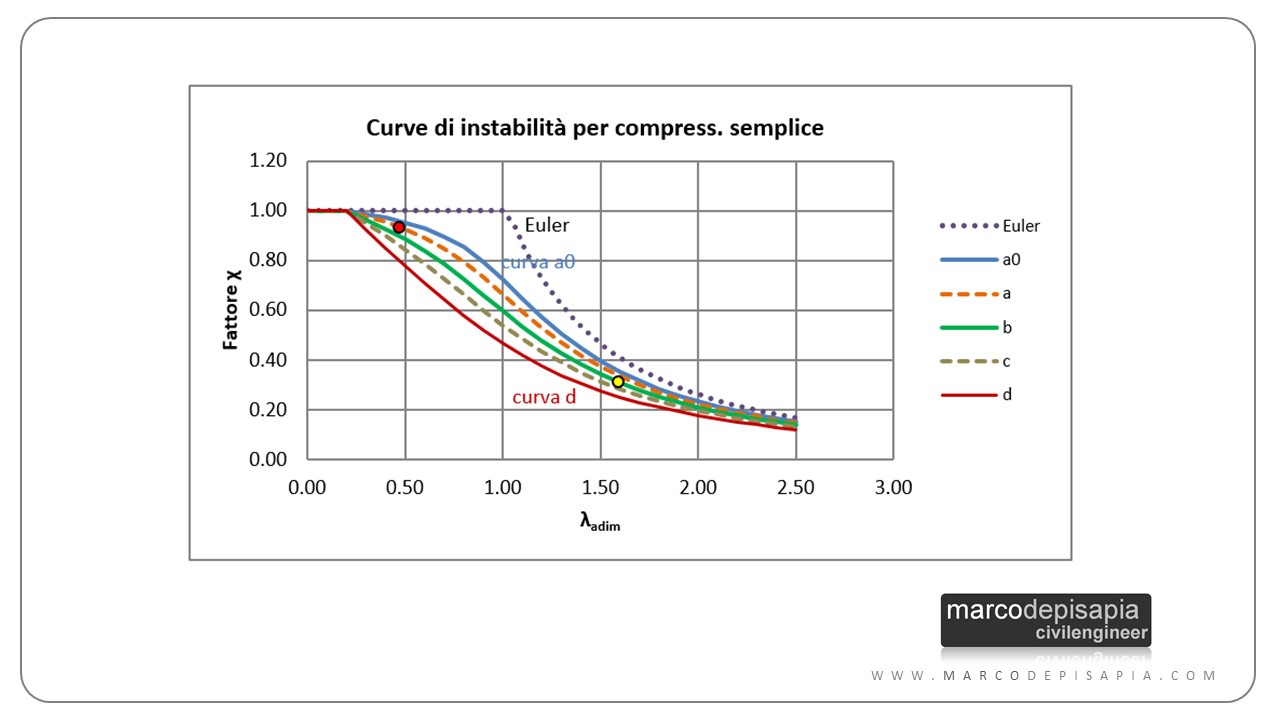
La differenza fra le curve sperimentali e la curva euleriana è dovuta al fatto che le curve sperimentali tengono conto dell’imperfezione geometrica delle aste. Come puoi vedere dal grafico, la curva euleriana è meno cautelativa rispetto alle curve di stabilità sperimentali. Ovvero per un dato valore della snellezza, la curva di stabilità euleriana fornisce un carico critico maggiore del reale carico critico ottenuto sperimentalmente.
Le curve di stabilità sperimentali proposte dalla Normativa Tecnica NTC2018 possono essere ottenute da una serie di formule matematiche in funzione dei seguenti parametri:
- il valore del carico critico euleriano;
- il fattore di imperfezioneα che a sua volta dipende da:
- classe di resistenza dell’acciaio;
- tipologia di sezione: a doppio T laminata o saldata, cava formata a freddo o a caldo, a T, a U, a L;
- limiti geometrici sullo spessore della flangia per le sezioni a doppio T;
- asse di inflessione y-y (asse forte) o z-z (asse debole).
Scarica Ver.Steel, l’app per il progetto e verifica di sezioni in acciaio

Per eseguire in maniera automatica il progetto e la verifica di stabilità delle aste in acciaio sottoposte al carico di punta ai sensi delle NTC2018 puoi scaricare gratuitamente Ver.Steel, l’app per l’analisi delle sezioni in acciaio. Compila i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download dell’applicazione.

Instabilità per carico di punta: scarica la risorsa utility per una simulazione interattiva
In questa risorsa utility puoi eseguire una simulazione interattiva del fenomeno dell’instabilità per carico di punta incrementando il carico assiale agente fino ad arrivare al carico critico di instabilità euleriana e visualizzare l’asta nella configurazione deformata.
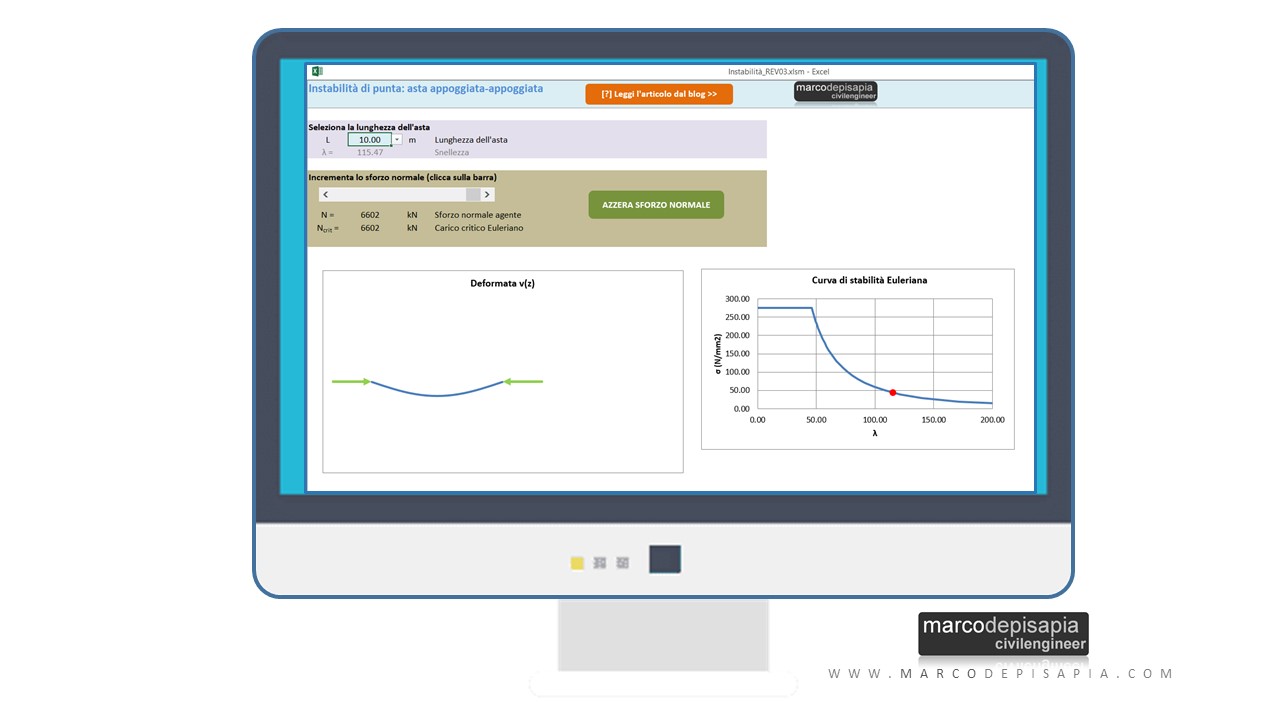
Per scaricare la risorsa utility sull’instabilità per carico di punta compila i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download.

Conclusioni
Spero che quest’articolo ti sia piaciuto e che l’esperimento dello spaghetto ti sia stato utile per comprendere l’instabilità delle aste snelle sottoposte ad un carico di punta. Se questo post ti è stato utile puoi suggerirlo ad un tuo collega su Linkedin o ad un tuo amico su Facebook cliccando sui tasti di condivisione social in fondo alla pagina. Ti è mai capitato di dover progettare una struttura in acciaio in cui l’instabilità per carico di punta era seriamente da tenere in conto? Puoi farmelo sapere lasciando un commento in basso.
Al prossimo articolo.
Marco
Aggiornato il 16/3/2020, pubblicato il 12/10/2015.

Pingback:Profili in acciaio: cosa sono le classi e come calcolarle