La verifica a torsione delle travi in acciaio richiede la determinazione del fattore di rigidezza torsionale Jt della sezione e il calcolo del valore massimo della tensione tangenziale da torsione. In quest’articolo vederemo:
- come calcolare il fattore di rigidezza torsionale Jt per le diverse tipologie di sezione;
- cos’è l’ingobbamento della sezione e perché si verifica;
- qual è la distribuzione delle tensioni tangenziali da torsione per ciascun tipo di sezione (piena, sottile, aperta o chiusa);
- come calcolare la tensione tangenziale massima di torsione.

Continua a leggere per saperne di più. Nel corso dell’articolo potrai scaricare Ver.Steel, un’utile applicazione implementata in Microsoft Excel (file xls) per il calcolo, progetto e verifica delle sezioni in acciaio.
Scarica Ver.Steel (xls di Microsoft Excel) per il progetto e verifica di sezioni in acciaio

Ver.Steel è l’app per il progetto e verifica di profili in acciaio implementata in Microsoft Excel. Puoi scaricare la versione gratuita dell’app compilando i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download.

Sezione circolare piena: fattore di rigidezza torsionale e tensione massima
La sezione circolare piena è il caso più semplice da analizzare nell’ambito della sollecitazione da torsione. Nella configurazione deformata la sezione subisce solo una rotazione nel proprio piano, senza alcuna deformazione fuori piano. La distribuzione delle tensioni tangenziali da torsione assume un andamento crescente linearmente dal centro del cerchio fino alla circonferenza.
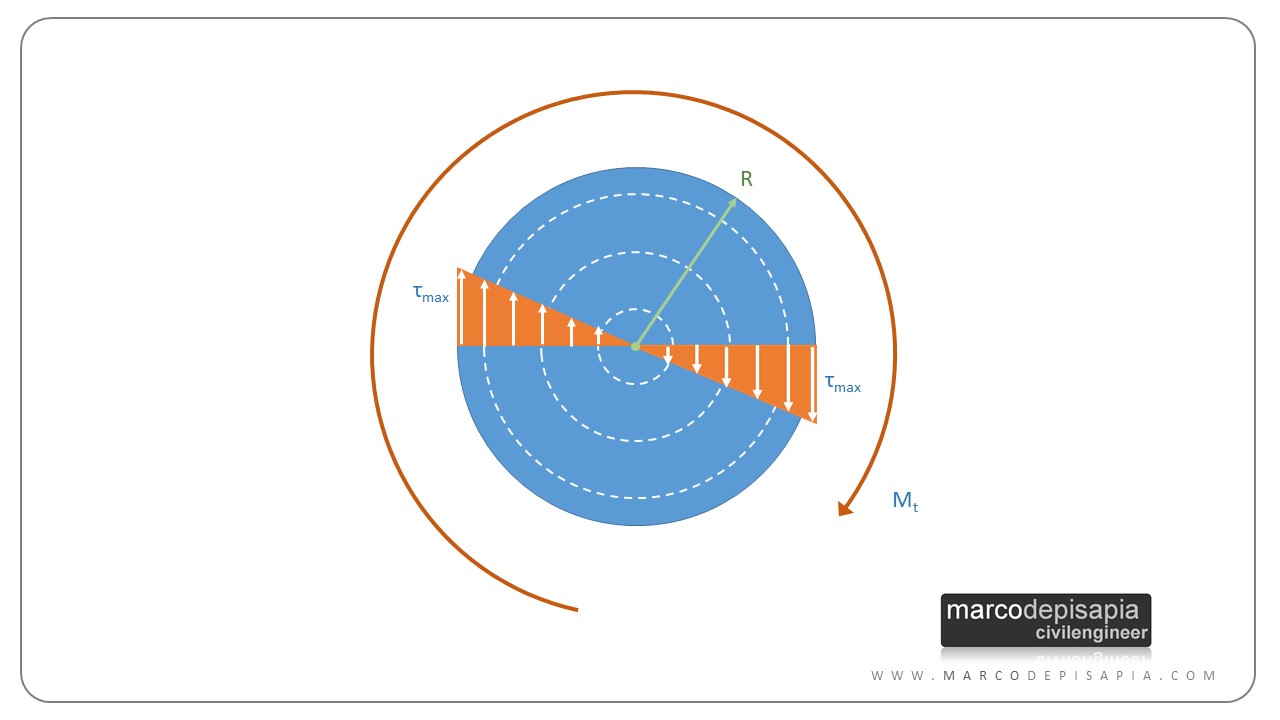
La formula per il calcolo della tensione tangenziale massima è la seguente:
τmax = (Mt / Jt) ⋅ R
- Mt = momento torcente sollecitante;
- Jt = fattore di rigidezza torsionale;
- R = raggio della sezione circolare.
Per la sezione circolare piena a causa dell’assenza del fenomeno di ingobbamento (ti spiego fra poco cos’è), il fattore di rigidezza torsionale coinciderà con il momento d’inerzia polare della sezione circolare.
Jt = Ip = π R4 /2
- Ip = momento d’inerzia polare della sezione.
Sezione circolare cava: fattore di rigidezza torsionale e tensione massima
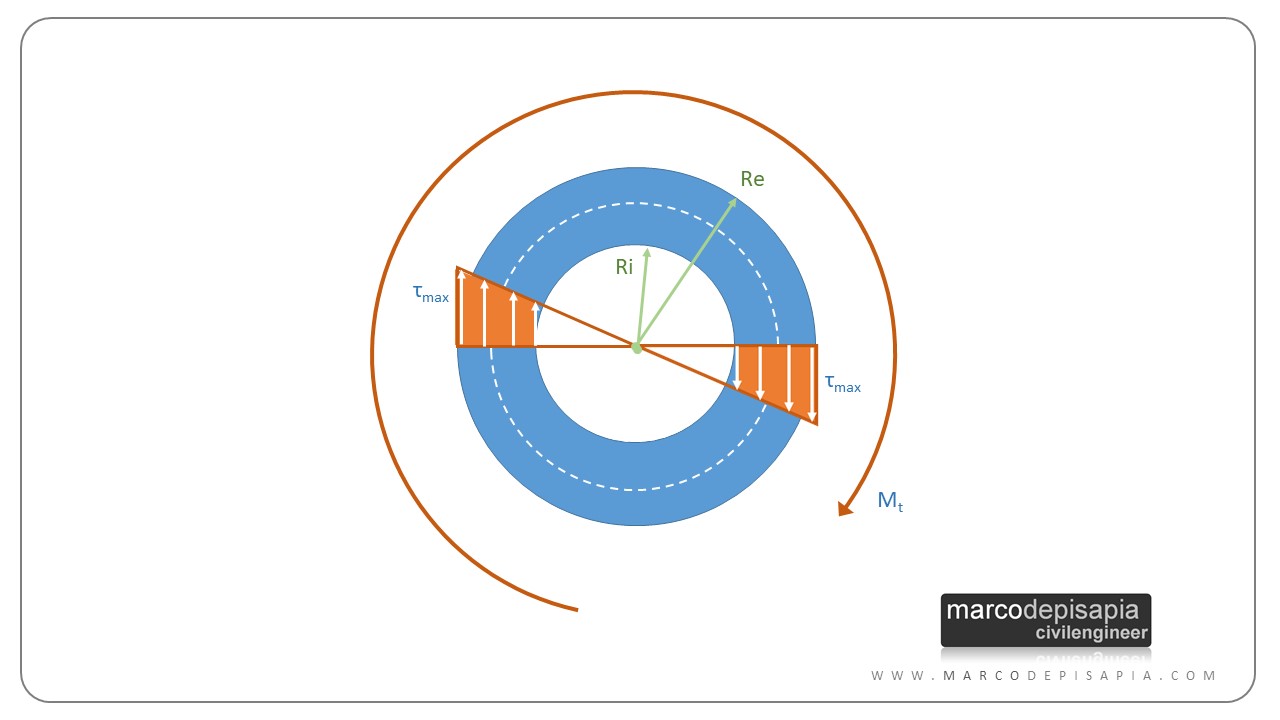
Lo stesso andamento delle tensioni tangenziali da torsione valido per la sezione circolare, lo si riscontra in maniera identica nella sezione circolare cava. In tal caso varia solo il valore del momento d’inerzia polare della sezione. La tensione tangenziale massima si avrà sempre in corrispondenza del bordo più esterno della sezione.
τmax = (Mt / Jt) ⋅ Re
Jt = Ip = π⋅(Re4 – Ri4)/2
- Re = raggio esterno della sezione
- Ri = raggio interno della sezione
Sezione rettangolare compatta: fattore di rigidezza torsionale e tensione massima
La tensione tangenziale massima da torsione si avrà sui lati lunghi, nelle zone più vicine al baricentro della sezione. Lungo le diagonali della sezione la tensione tangenziale parte da un valore nullo in corrispondenza del baricentro per poi crescere e assumere di nuovo valore nullo in corrispondenza degli spigoli della sezione. A differenza della sezione circolare in cui lungo il bordo la tensione tangenziale era sempre tangente alla circonferenza, per le sezioni rettangolari in corrispondenza degli spigoli la tensione tangenziale dovrà assumere valore nullo per non violare la condizione di tangenza lungo i bordi della sezione.
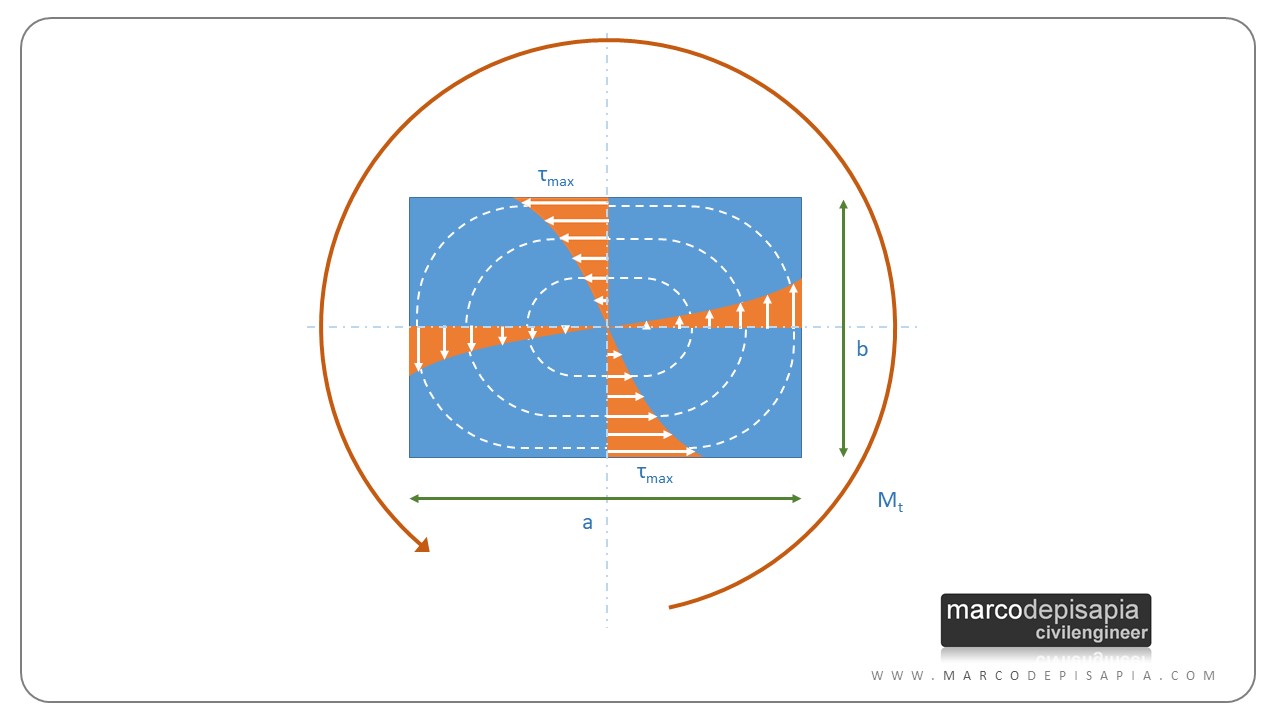
I punti della sezione rettangolare per effetto del momento torcente subiranno degli spostamenti fuori piano dando vita al fenomeno dell’ingobbamento.
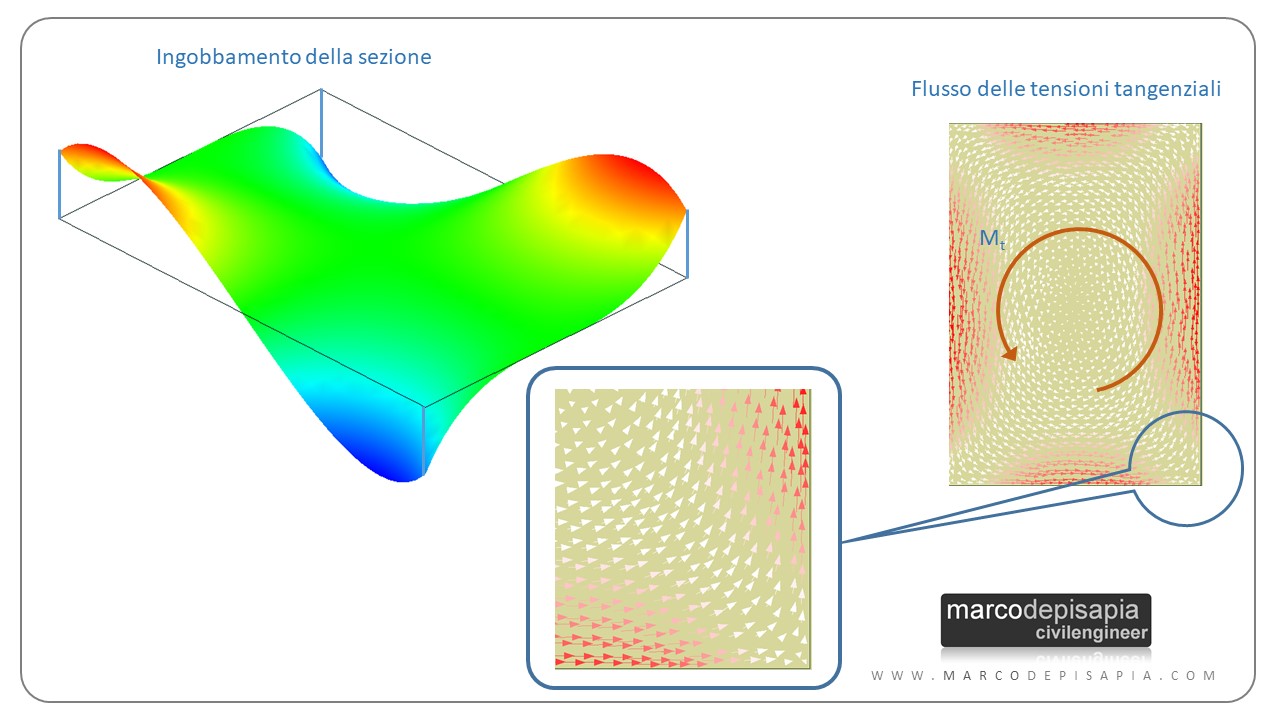
Il calcolo della tensione tangenziale massima sarà dato dalla formula seguente:
τmax = (2⋅Mt / Jt) ⋅ b/2 = (Mt / Jt) ⋅ b
- b = lato minore della sezione rettangolare.
Per le sezioni rettangolari si può utilizzare una formula semplificata per il calcolo del fattore di rigidezza torsionale Jt che utilizza il parametro α da valutare in funzione del rapporto fra i lati della sezione.
Jt = α ⋅ a ⋅ b3
- a = lato maggiore della sezione;
- b = lato minore della sezione rettangolare;
- α = coefficiente funzione del rapporto a/b.
Valori di α in funzione del rapporto a/b
| a/b | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 5 | 10 | ∞ |
| α | 0.141 | 0.166 | 0.196 | 0.229 | 0.249 | 0.263 | 0.291 | 0.312 | 0.333 |
Sezione rettangolare sottile: fattore di rigidezza torsionale e tensione massima
Per le sezioni rettangolari sottili caratterizzate da una dimensione prevalente rispetto all’altra la teoria della torsione è la stessa valida per le sezioni rettangolare compatte, ma con una differenza. Le linee di flusso delle tensioni tangenziali da torsione avranno andamento rettilineo e parallelo al lato lungo della sezione, ad eccezione delle due piccole parti terminali della sezione in cui le tensioni tangenziali non saranno più parallele al lato lungo.
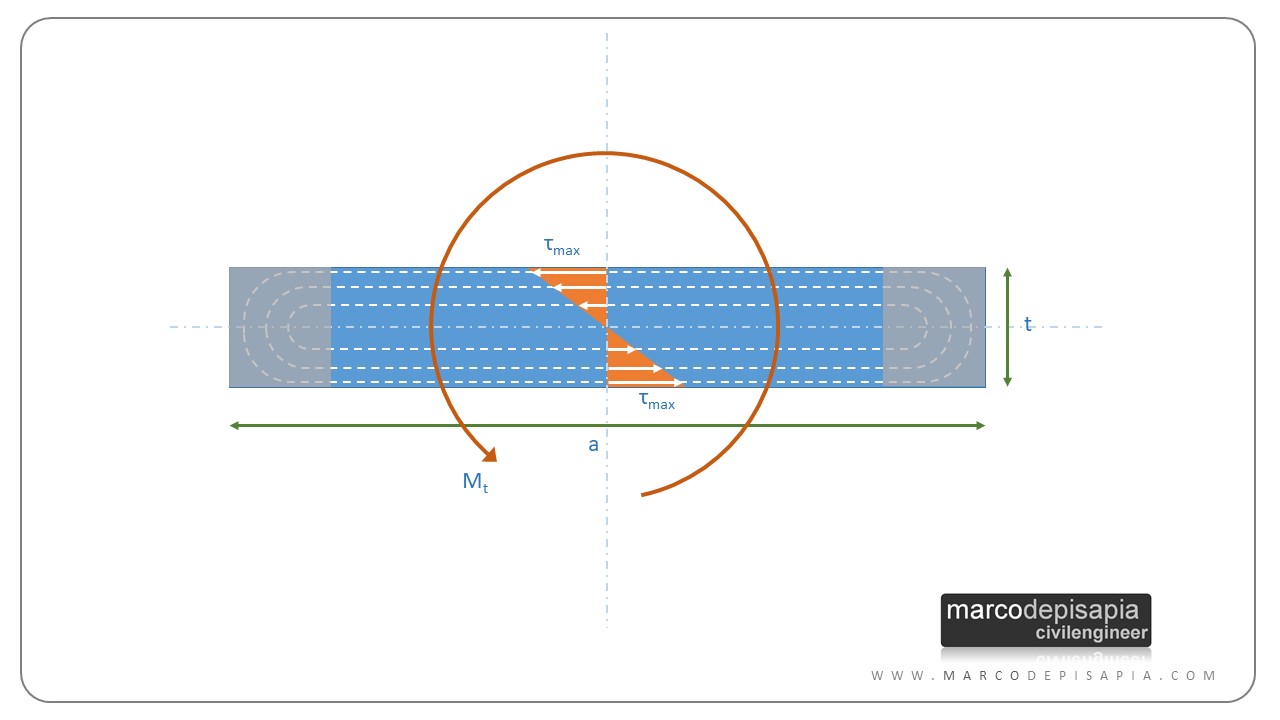
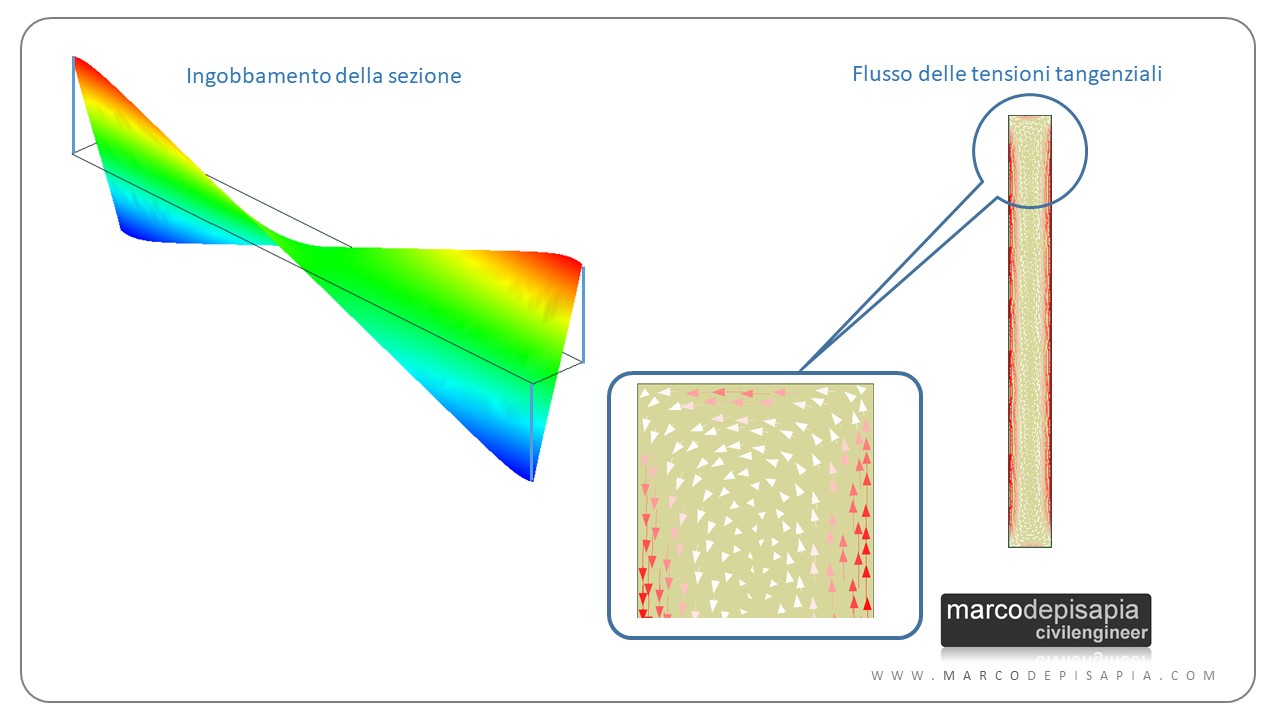
La tensione tangenziale massima si avrà in corrispondenza del bordo del lato lungo della sezione e si calcolerà con la seguente formula:
τmax = (2⋅Mt / Jt) ⋅ t/2 = (Mt / Jt) ⋅ t
Jt = 1/3⋅ a ⋅ t3
- t = spessore della sezione sottile;
- a = lunghezza della sezione sottile.
Per le sezioni sottili il rapporto fra i lati a/b si può assumere tendente ad infinito. Pertanto il fattore α per il calcolo di Jt sarà pari a 0.33 ovvero a 1/3, come riportato nella tabella precedente.
Sezione sottile aperta
Le formule viste per la sezione rettangolare sottile possono essere adoperate anche per le sezioni sottili aperte di forma generica e spessore costante. Di fatto le tensioni tangenziali da torsione per una sezione rettangolare sottile non cambiano significativamente se la sezione viene comunque ripiegata.
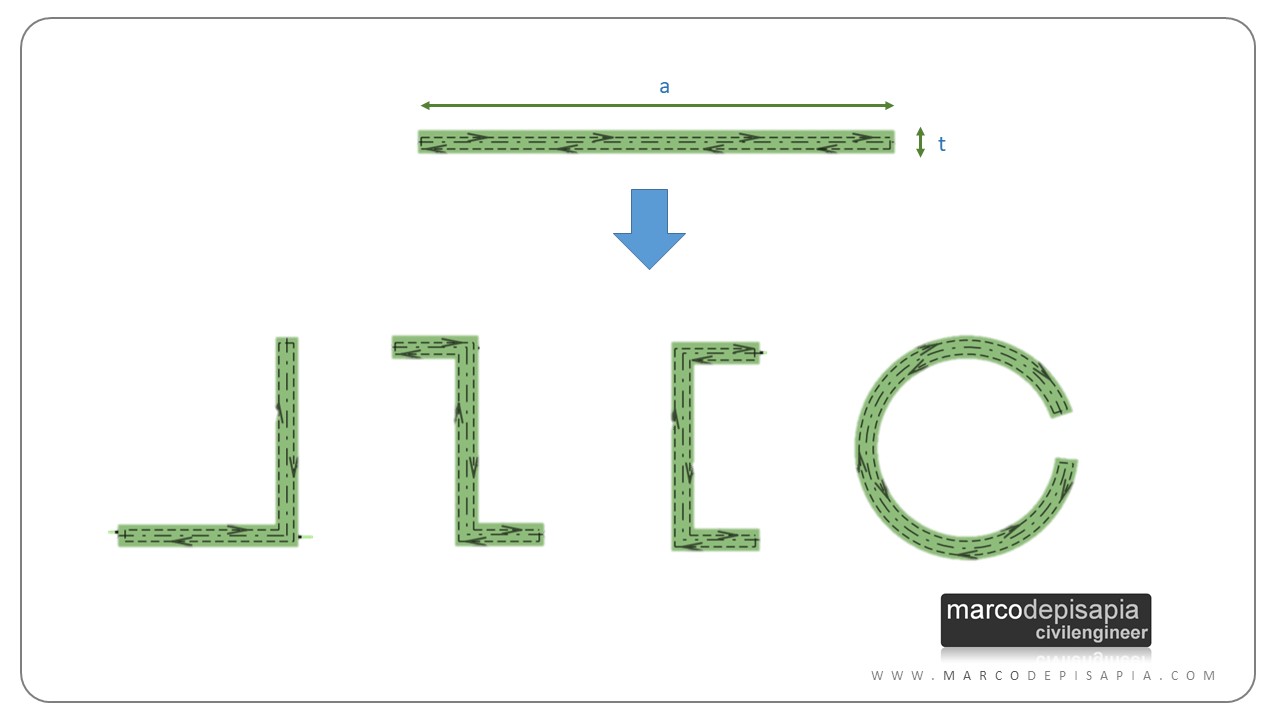
La tensione tangenziale massima può essere calcolata secondo la seguente formula:
τmax = (2⋅Mt / Jt) ⋅ t/2 = (Mt / Jt) ⋅ t
Jt = 1/3⋅ a ⋅ t3
- t = spessore della sezione sottile;
- a = lunghezza della linea media della sezione sottile.
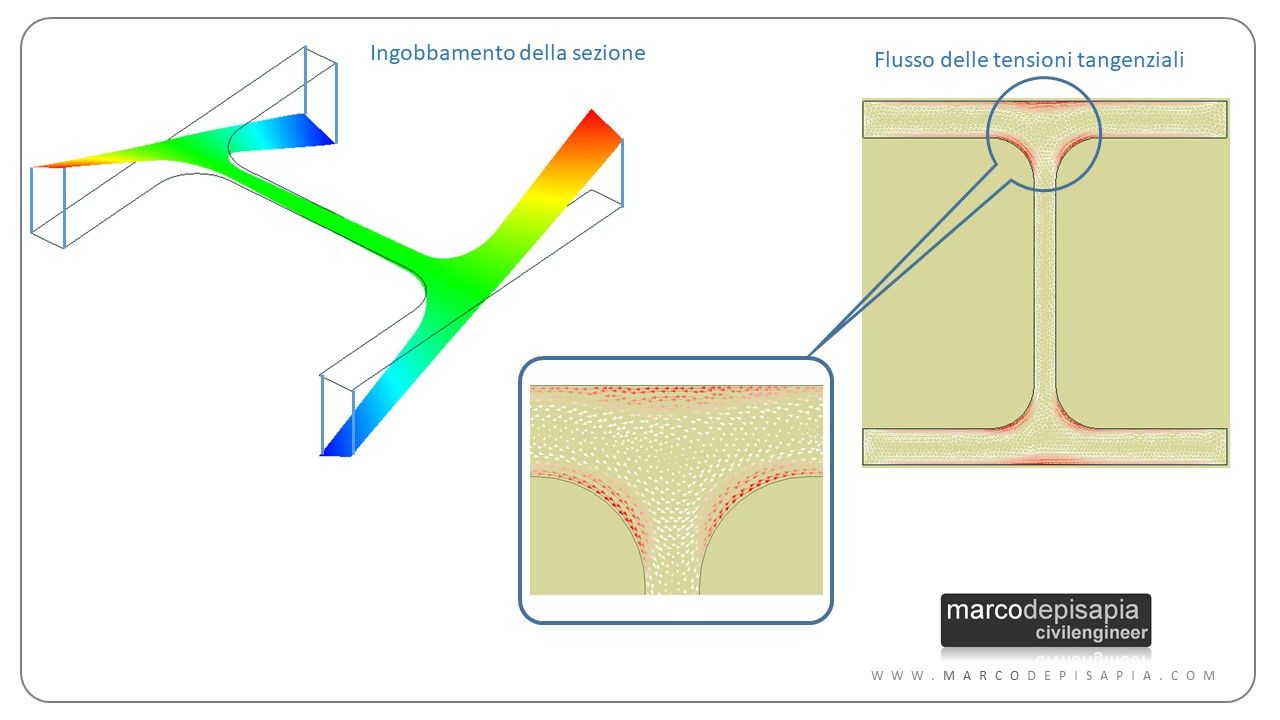
Per le sezioni composte dall’unione di rettangoli sottili di spessore differente come per esempio le sezioni a doppio T (IPE, HEA, HEB etc.) il fattore di rigidezza torsionale sarà dato dalla seguente sommatoria:
Jt = 1/3⋅ Σi (ai ⋅ ti3)
τmax = (2⋅Mt / Jt) ⋅ t/2 = (Mt / Jt) ⋅ tmax
- ti = spessore del rettangolo i-esimo della sezione;
- ai = lunghezza del rettangolo i-esimo della sezione.
La tensione tangenziale massima si avrà nel rettangolo di spessore maggiore.
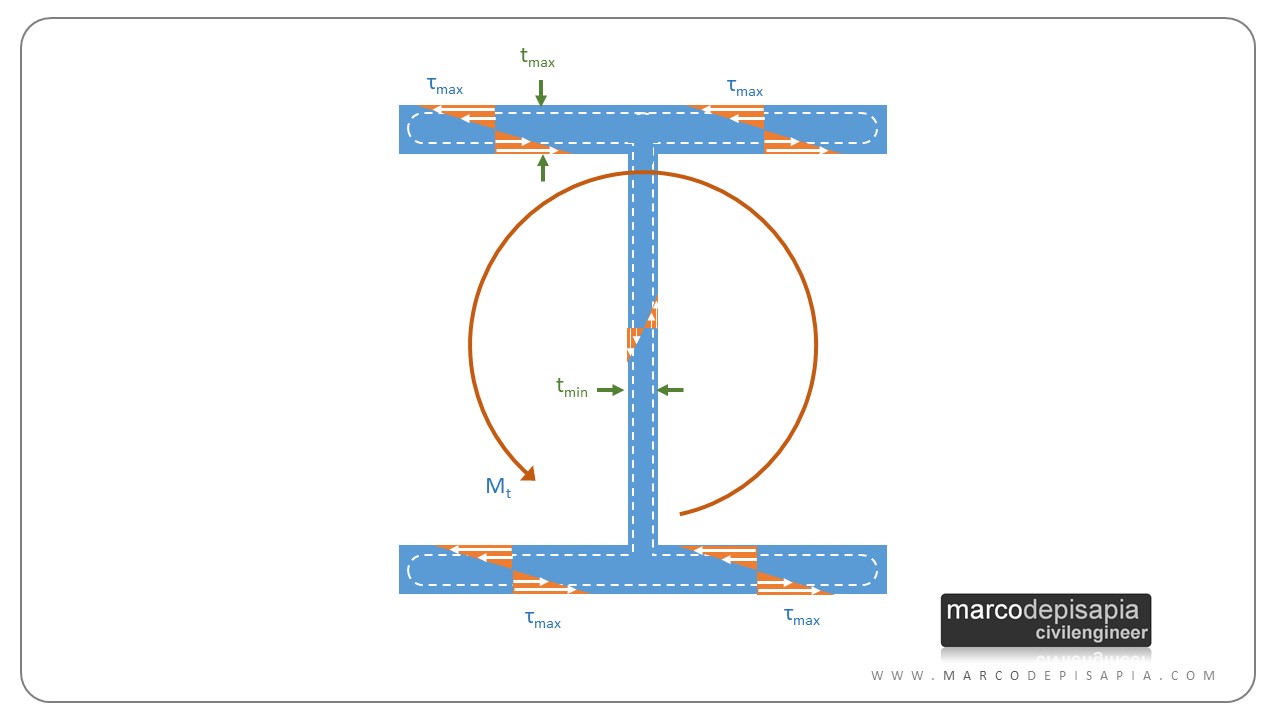
Sezione sottile chiusa
Il modo di resistere alle sollecitazioni da torsione delle sezioni chiuse è profondamente diverso rispetto a quello delle sezioni aperte. Nelle sezioni aperte le tensioni tangenziali variano linearmente lungo lo spessore, assumendo valore nullo in corrispondenza della linea media e valori di segno opposto ai due lati della linea media. Questo accade perché le linee di flusso delle tensioni tangenziali dovranno creare un circuito chiuso nello spessore della sezione sottile.
Per le sezioni sottili chiuse invece la line media forma già di per sé un circuito chiuso e pertanto le linee di flusso delle tensioni tangenziali seguiranno la linea media e le tensioni tangenziali avranno un valore costante lungo lo spessore dell’elemento.
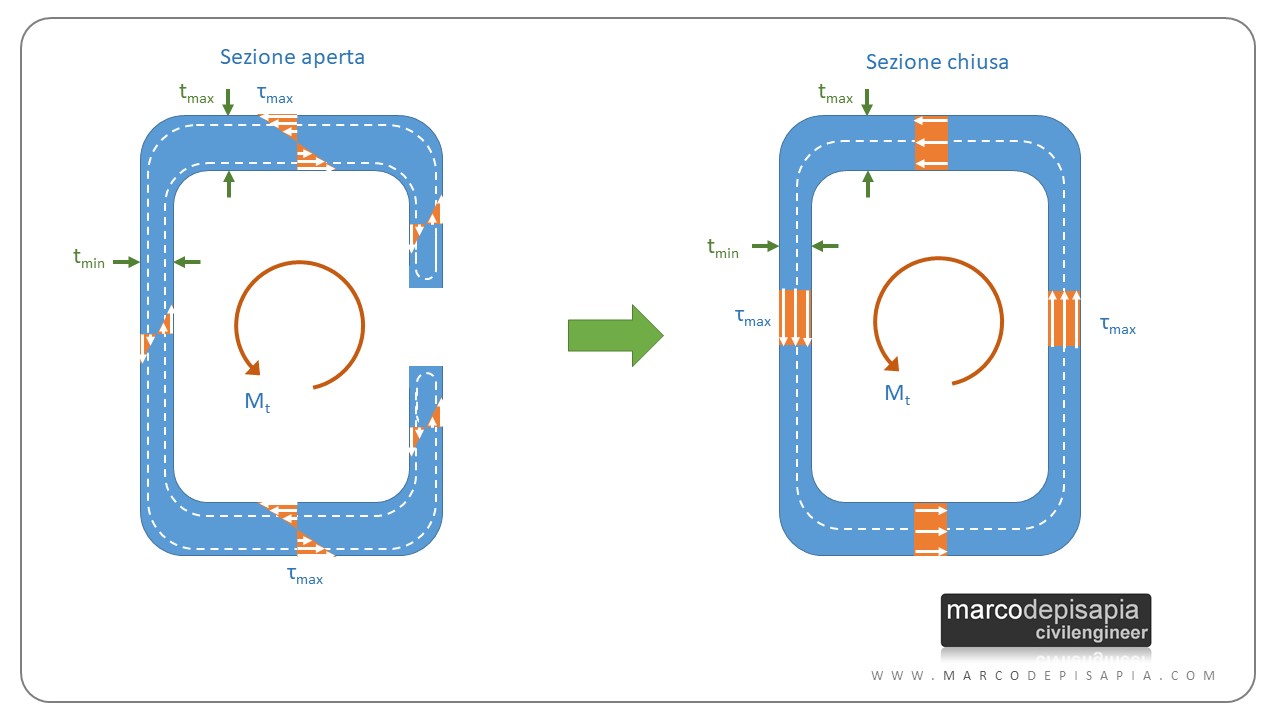
La tensione tangenziale massima per le sezioni sottili chiuse si avrà nell’elemento di spessore minore, a differenza di quanto accade per le sezioni sottili aperte in cui la tensione tangenziale massima sarà nell’elemento di spessore maggiore.
ll calcolo della tensione tangenziale massima può essere eseguito mediante la formula di Bredt:
τmax = Mt / (2 ⋅ Ω ⋅ tmin)
- Ω = area racchiusa dalla linea media della sezione sottile chiusa;
- tmin = spessore minimo della sezione sottile chiusa.
Per le sezioni sottili chiuse il calcolo del fattore di rigidezza torsionale Jt si esegue mediante la seguente formula:
Jt = 4 Ω2 / ( ∫1/t(s) ds )
- Ω = area racchiusa dalla linea media della sezione;
- t(s) = spessore variabile della sezione sottile chiusa in funzione dell’ascissa curvilinea s.
Se lo spessore della sezione sottile chiusa è costante, il fattore di rigidezza torsionale diventa:
Jt = 4 ⋅ Ω2 ⋅ t / Lγ
- Ω = area racchiusa dalla linea media della sezione;
- t = spessore costante della sezione sottile chiusa;
- Lγ = lunghezza della linea media della sezione sottile chiusa.
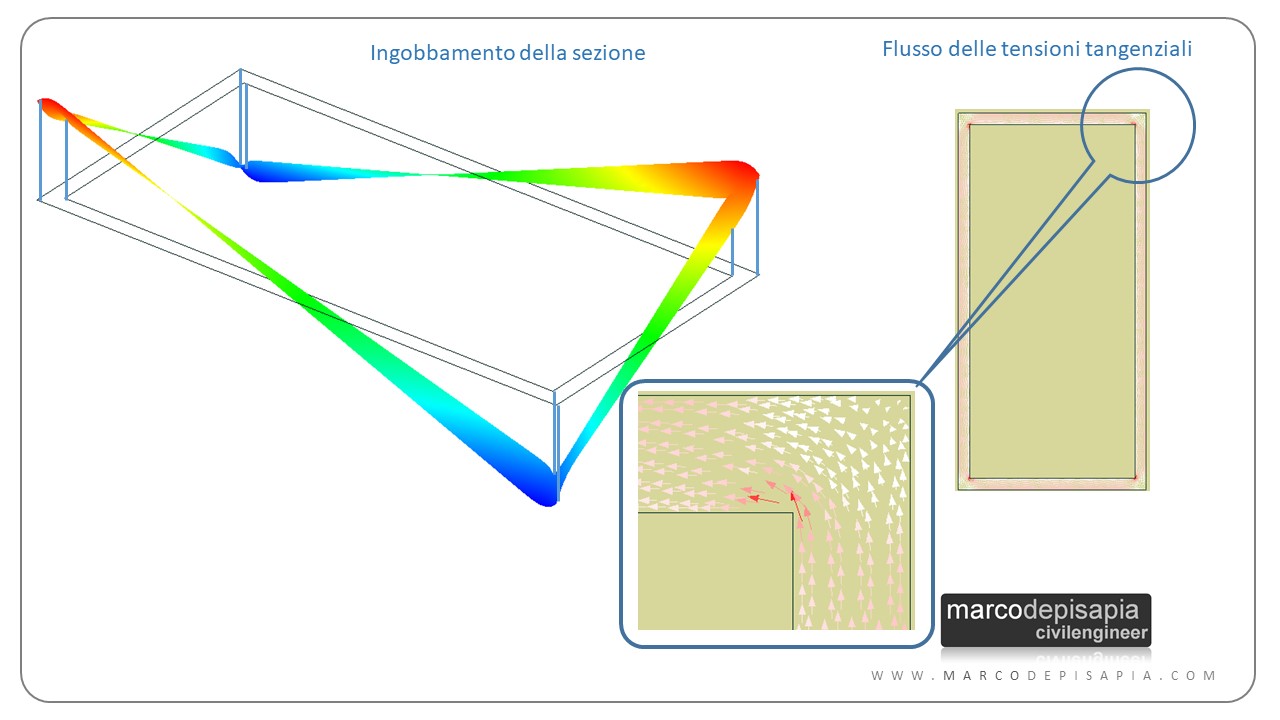
Ingobbamento da torsione e fattore di rigidezza torsionale
Nelle sezioni circolari le tensioni tangenziali agenti sul bordo della sezione risultano essere sempre tangenti alla circonferenza. Questa condizione determina l’assenza dell’ingobbamento della sezione, ovvero dello spostamento fuori piano dei punti della sezione.
Per sezioni di forma diversa da quella circolare le tensioni tangenziali in corrispondenza degli spigoli, non potendo essere tangenti al bordo della sezione, dovranno essere per forza nulle, dando vita all’ingobbamento della sezione ovvero a deformazioni fuori piano della sezione, in maniera analoga a quanto accade in presenza delle tensioni tangenziali da taglio.
Il fattore di rigidezza torsionale dipende dalla distribuzione dell’area della sezione rispetto agli assi principali d’inerzia x e y e dalla funzione di ingobbamento che descrive lo spostamento fuori piano di ogni punto della sezione per effetto delle tensioni tangenziali da torsione. La formula analitica completa per il calcolo del fattore di rigidezza torsionale è la seguente:
Jt = ∫(x2 + y2 + x ⋅ ∂ω/∂y – y ⋅ ∂ω/∂x) dA
- ω(x,y) = funzione di ingobbamento della sezione.
In assenza di ingobbamento (ω=0) il fattore di rigidezza torsionale coinciderà con il momento d’inerzia polare della sezione.
ω = 0 ⇒ Jt = ∫(x2 + y2) dA = Ip (momento d’inerzia polare)
Per una trattazione analitica completa sul problema della torsione e sul calcolo del fattore di rigidezza torsionale ti suggerisco il libro di testo Lezioni di scienza delle costruzioni di Michele Capurso.
La presenza dell’ingobbamento nelle sezioni diverse dalla sezione circolare rende complesso il calcolo del fattore di rigidezza torsionale Jt. Per sezioni dalla forma particolare potrebbe essere necessario utilizzare appositi software di analisi ad elementi finiti per la determinazione del fattore di rigidezza torsionale Jt. Per le sezioni sottili di uso più comune sono disponibili le formule semplificate che ti ho mostrato in quest’articolo per il calcolo del fattore di rigidezza torsionale.
Scarica Ver.Steel, l’app per il progetto e verifica di sezioni in acciaio

Per eseguire in maniera automatica il progetto e verifica delle sezioni in acciaio puoi scaricare gratuitamente Ver.Steel, l’app per l’analisi delle sezioni in acciaio. Compila i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download dell’applicazione.

Torsione delle travi: quale sezione scegliere? Rigidezze torsionali a confronto
Abbiamo visto finora l’andamento delle tensioni tangenziali, le tensioni massime e le formule per il calcolo del fattore di rigidezza torsionale per le sezioni di uso più comune nella pratica tecnica. Ma in sostanza quale sezione conviene utilizzare quando le sollecitazioni da torsione hanno un ruolo prevalente? Per darti un parametro di confronto fra le rigidezze torsionali delle diverse sezioni ti riporto un confronto fra i fattori di rigidezza torsionale per diversi tipi di sezione di dimensioni confrontabili (sono tutte contenute in un quadrato 100 x 100 mm).
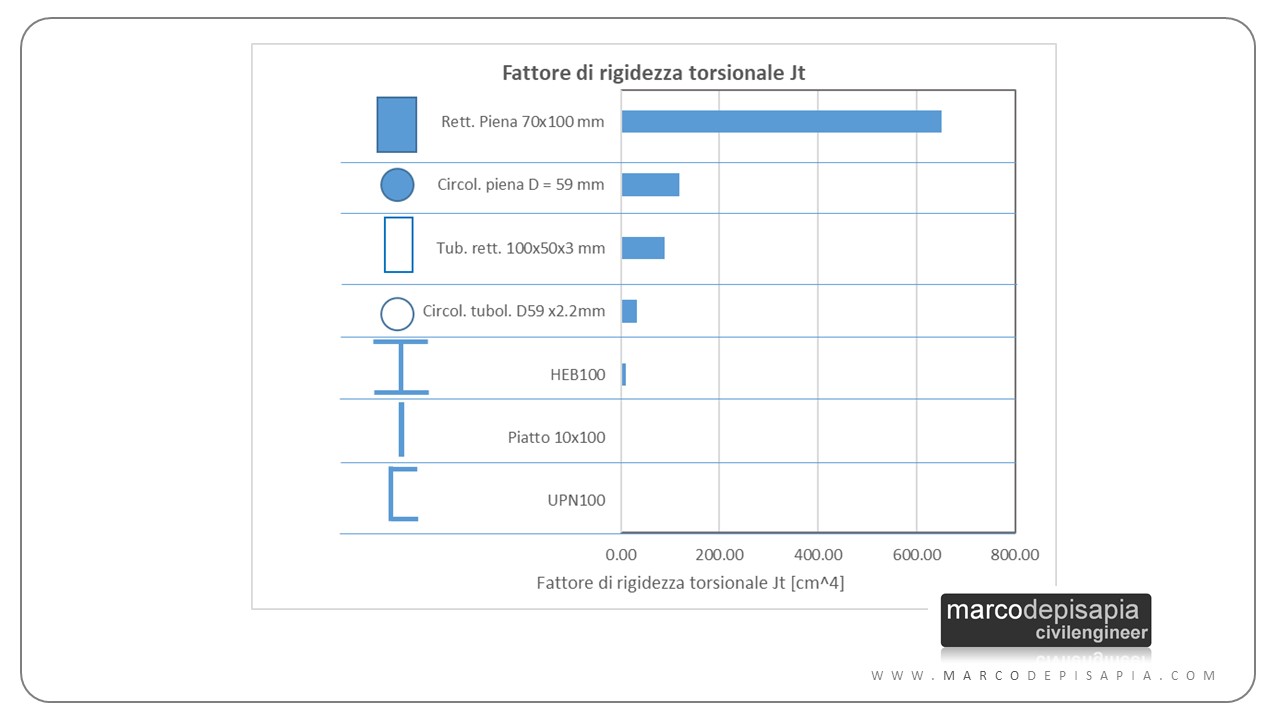
Come puoi vedere le sezioni piene rettangolari e circolari hanno rigidezze torsionali molto elevate rispetto alle sezioni in parete sottile. Ma per le sezioni in acciaio sarebbe anti-economico utilizzare sezioni piene. Ti riporto pertanto il confronto relativamente alle sole sezioni in parete sottile.
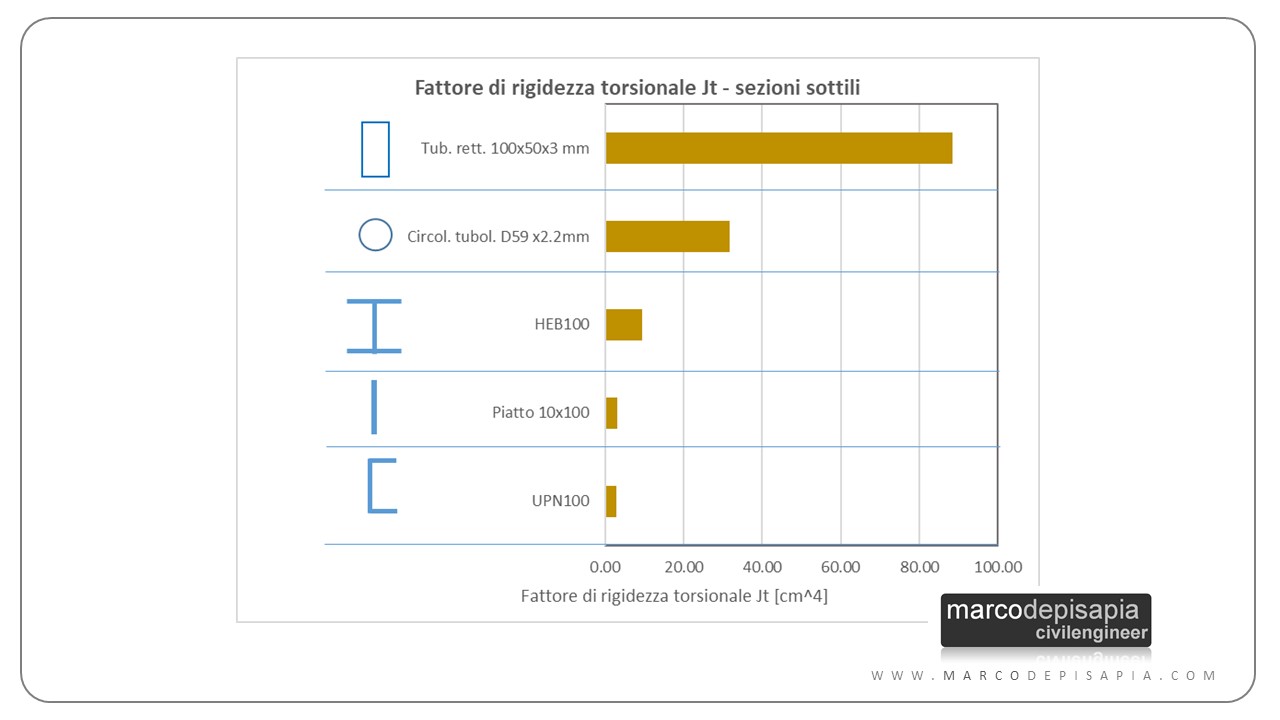
Dal grafico a barre riportato sopra risulta evidente che, in presenza di sollecitazioni da torsione non trascurabili, i profili a doppio T, ad U e i piatti sono assolutamente da evitare.
Conclusioni
Il calcolo del fattore di rigidezza torsionale molto spesso genera confusione fra i progettisti di strutture. Il fattore di rigidezza torsionale è necessario anche per la verifica all’instabilità flesso-torsionale dei profili sottili. A volte tale valore si trova tabellato nei sagomari dei profili in acciaio, ma non sempre. In questi casi conoscere le formule necessarie per il calcolo del fattore di rigidezza torsionale Jt ti permetterà di eseguire le verifiche necessarie senza ricorrere a software di analisi più avanzata.
L’articolo di oggi finisce qui. Mi auguro sia stato d’aiuto per comprendere cos’è l’ingobbamento da torsione e come calcolare il fattore di rigidezza torsionale delle sezioni sottili in acciaio. Se l’hai trovato utile, puoi suggerirlo ad un tuo collega su Linkedin o ad un tuo amico su Facebook cliccando sui tasti di condivisione social in fondo alla pagina.
Al prossimo post.
Marco
Risorsa consigliata
Per approfondire la trattazione analitica del problema di torsione ti suggerisco il libro di testo Lezioni di scienza delle costruzioni di Michele Capurso.
Pubblicato in data: 2/3/2020. Repost: 28/8/2023


Si è verificato un errore. Controlla l’indirizzo web della pagina. Se contiene “marcodepisapia.altervista.org”, sostituiscilo con “marcodepisapia.com”, ricarica la pagina e riprova. Se l’errore persiste contatta l’amministratore del sito.
non riesco a scaricare le risorse
Il modulo per il download mi risulta normalmente funzionante.
Prova con un indirizzo email differente.
Ciao
Marco
Informazioni precise e complete.
Grazie
Grazie del commento Claudio 🙂