Effetti del secondo ordine: come calcolarli senza eseguire analisi complesse

Quando esegui il calcolo di una struttura, dopo aver calcolato le sollecitazioni e gli spostamenti di impalcato in combinazione sismica, potrebbe essere necessario portare in conto i cosiddetti effetti del secondo ordine. Gli effetti del secondo ordine possono determinare un incremento delle sollecitazioni sismiche che può essere compreso fra l’11% e il 25%. Non si tratta certo di un incremento di poco conto.

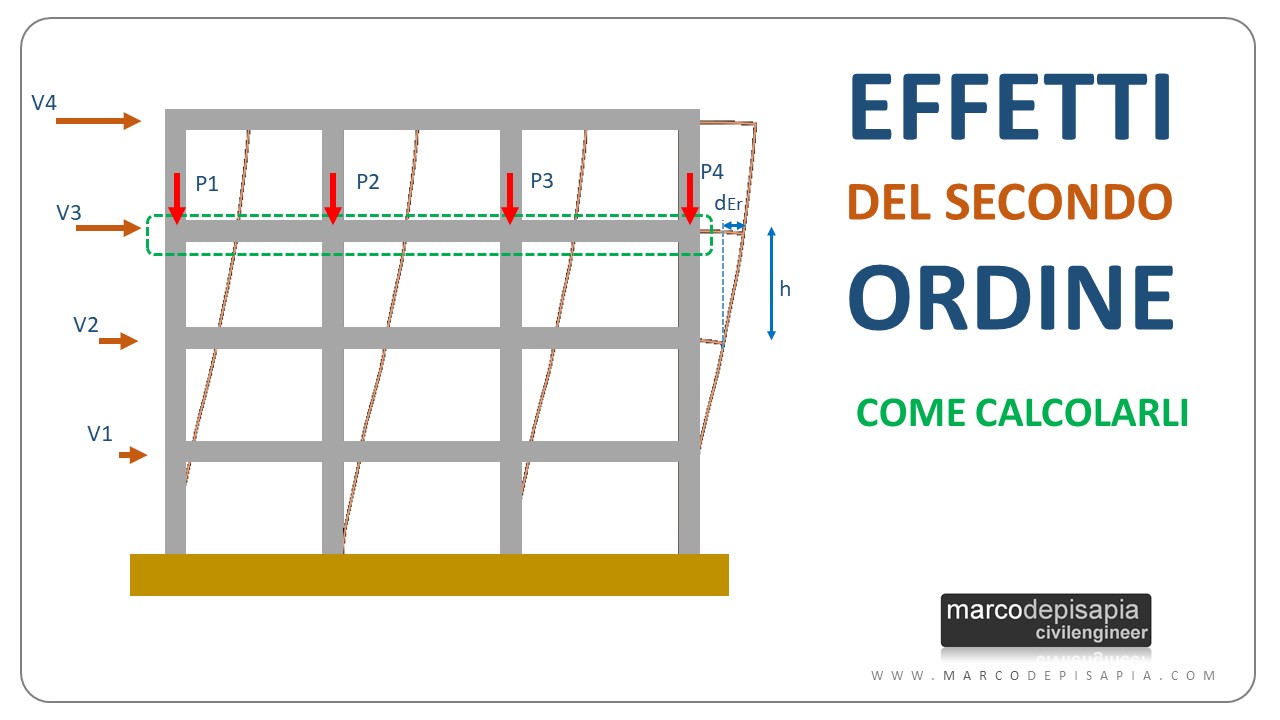
L’entità degli effetti del secondo ordine dipende dalla rigidezza laterale della struttura che hai progettato. Se la tua struttura è molto deformabile lateralmente, tali effetti potrebbero non essere trascurabili. L’incremento delle sollecitazioni che ne deriva può essere valutato in maniera semplificata attraverso il parametro θ [theta]. Questo numeretto è in grado di dirci se gli effetti del secondo ordine sono trascurabili oppure no e se è necessario incrementare le sollecitazioni sismiche per tenerne conto, se bisogna eseguire un’analisi del secondo ordine (vedremo dopo cos’è) o addirittura se bisogna riprogettare la struttura rendendola più rigida nei confronti delle azioni orizzontali. 

Nel post di oggi ti spiego:

• cosa sono gli effetti del secondo ordine;
• quando è necessario portarli in conto in un calcolo strutturale;
• cos’è il parametro θ e come si calcola;
• che tipo di analisi eseguire per tener conto degli effetti del secondo ordine.

Analisi del secondo ordine: le non linearità geometriche

La Normativa Tecnica NTC2018 definisce due tipologie di analisi:

• l’analisi del primo ordine: si esegue imponendo l’equilibrio sulla configurazione iniziale indeformata della struttura;
• l’analisi del secondo ordine:  impone l’equilibrio sulla configurazione deformata della struttura per effetto dei carichi applicati.

In pratica nell’analisi del primo ordine alla struttura indeformata vengono applicati i carichi agenti e calcolate le deformazioni, gli spostamenti e le sollecitazioni.

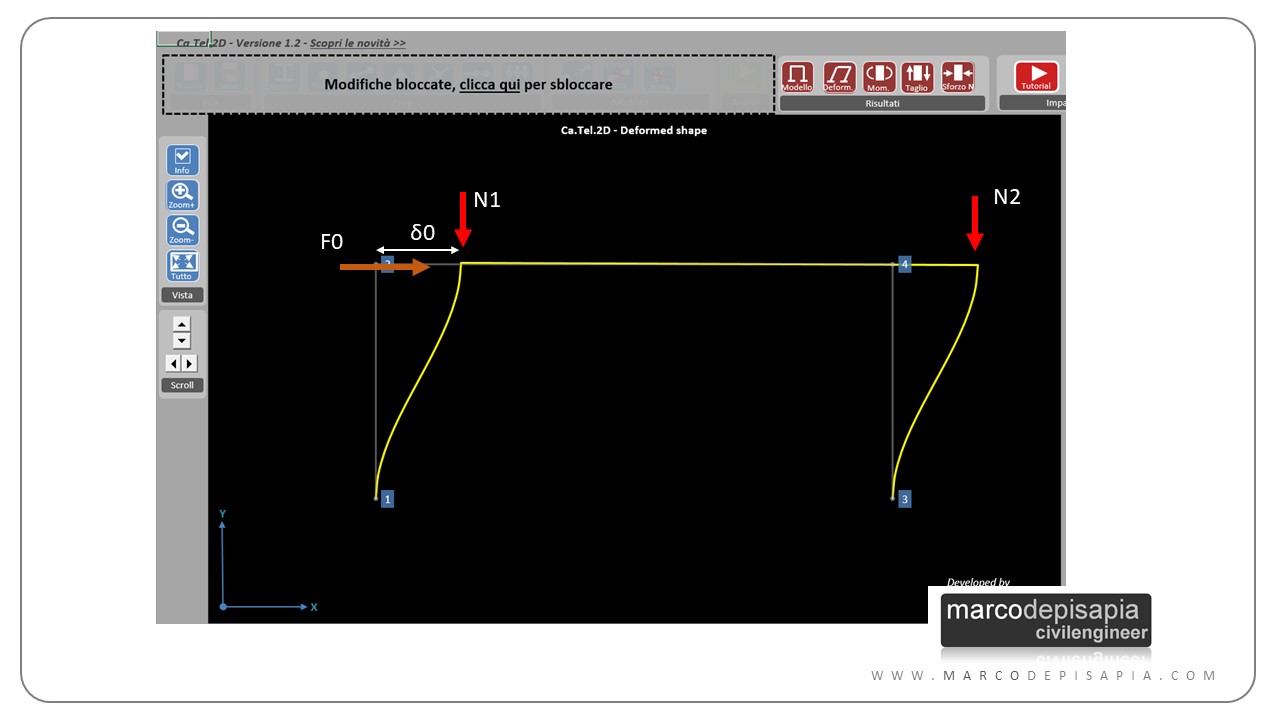
Ma in realtà, una volta che la struttura si trova nella sua configurazione deformata, i carichi applicati continuano ad esercitare la loro azione. Ci sono casi in cui i carichi agenti sulla configurazione deformata della struttura determinano un incremento delle sollecitazioni e degli spostamenti. Ti mostro di seguito un esempio per illustrarti gli effetti del secondo ordine per un telaio piano. Il telaio dell’esempio è stato calcolato utilizzando Ca.Tel.2D, l’applicazione del blog per il calcolo di modelli strutturali piani (puoi scaricare l’applicazione gratuitamente a questo link). Il telaio è caricato da forze orizzontali concentrate nei nodi e carichi distribuiti sulle travi.

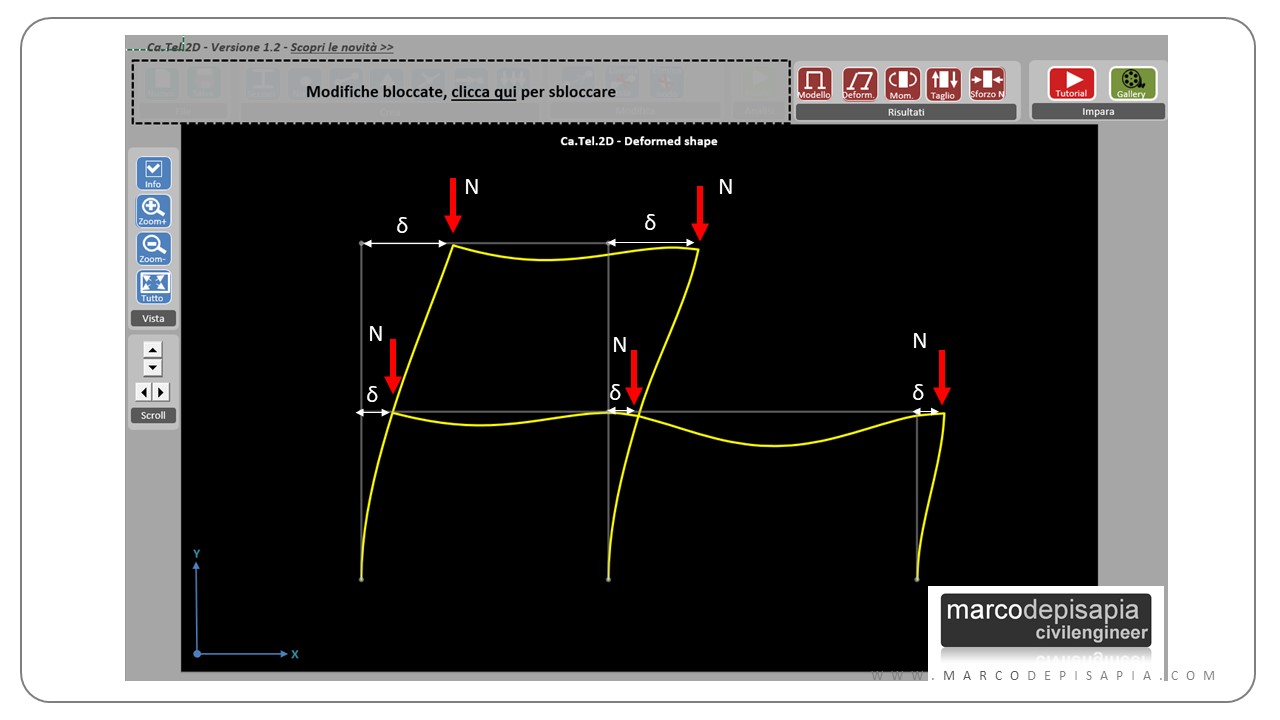
Per effetto delle forze concentrate orizzontali, i traversi esibiscono uno spostamento orizzontale δ. Lo spostamento relativo fra la testa e il piede dei pilastri e gli sforzi normali agenti determinano un incremento del momento flettente e di conseguenza dello spostamento relativo (vedi immagine sopra).

Gli effetti del secondo ordine, ovvero le sollecitazioni che derivano considerando i carichi agenti sulla configurazione deformata della struttura, possono essere trascurati se l’incremento delle sollecitazioni del primo ordine è inferiore al 10%. Lo prescrive la Normativa Tecnica NTC2018 al par. 4.1.1.4.

Gli effetti del secondo ordine possono essere trascurati se sono inferiori al 10% dei corrispondenti effetti del primo ordine […]

par. 4.1.1.4 delle NTC2018

Ma come capire se tale incremento è inferiore oppure no al 10%? Dobbiamo per caso eseguire un’analisi del secondo ordine considerando le non linearità geometriche? Fortunatamente la Normativa Tecnica ci consente di seguire una strada semplificata. E’ qui che entra in gioco il parametro θ [theta]. Seguimi per capire di cosa si tratta. 

Il parametro θ: l’alternativa all’analisi del secondo ordine

Una volta completata l’analisi del primo ordine, in cui le sollecitazioni vengono calcolate considerando la struttura indeformata, bisognerebbe valutare gli effetti del secondo ordine, per capire se tali effetti sono trascurabili ovvero se inferiori al 10%, calcolando le sollecitazioni sulla struttura deformata.

Non tutti software di calcolo sono dotati di un algoritmo in grado di eseguire analisi del secondo ordine (per esempio l’analisi P-Delta). Eseguire una doppia analisi sarebbe un ulteriore onere computazionale ed un’ulteriore complicazione nell’elaborazione del nostro calcolo strutturale. In questo caso la normativa ci viene incontro. E’ possibile infatti utilizzare una strada semplificata, amplificando di una certa quantità le sollecitazioni sismiche per tener conto degli effetti del secondo ordine. Ma di quanto vanno amplificate le sollecitazioni? Ce lo dice il parametro θ definito di seguito:

θ = (P ⋅ dEr) / (V ⋅ h)

formula [7.3.3] delle NTC2018

• P = carico verticale totale dovuto all’orizzontamento in esame e alla struttura sovrastante;
• dER è lo spostamento orizzontale medio d’interpiano allo SLV, ottenuto come differenza tra lo spostamento orizzontale dell’orizzontamento considerato e lo spostamento orizzontale dell’orizzontamento immediatamente sottostante;
• V è la forza orizzontale totale in corrispondenza dell’orizzontamento in esame, derivante dall’analisi lineare con fattore di comportamento q;
• h è la distanza tra l’orizzontamento in esame e quello immediatamente sottostante.

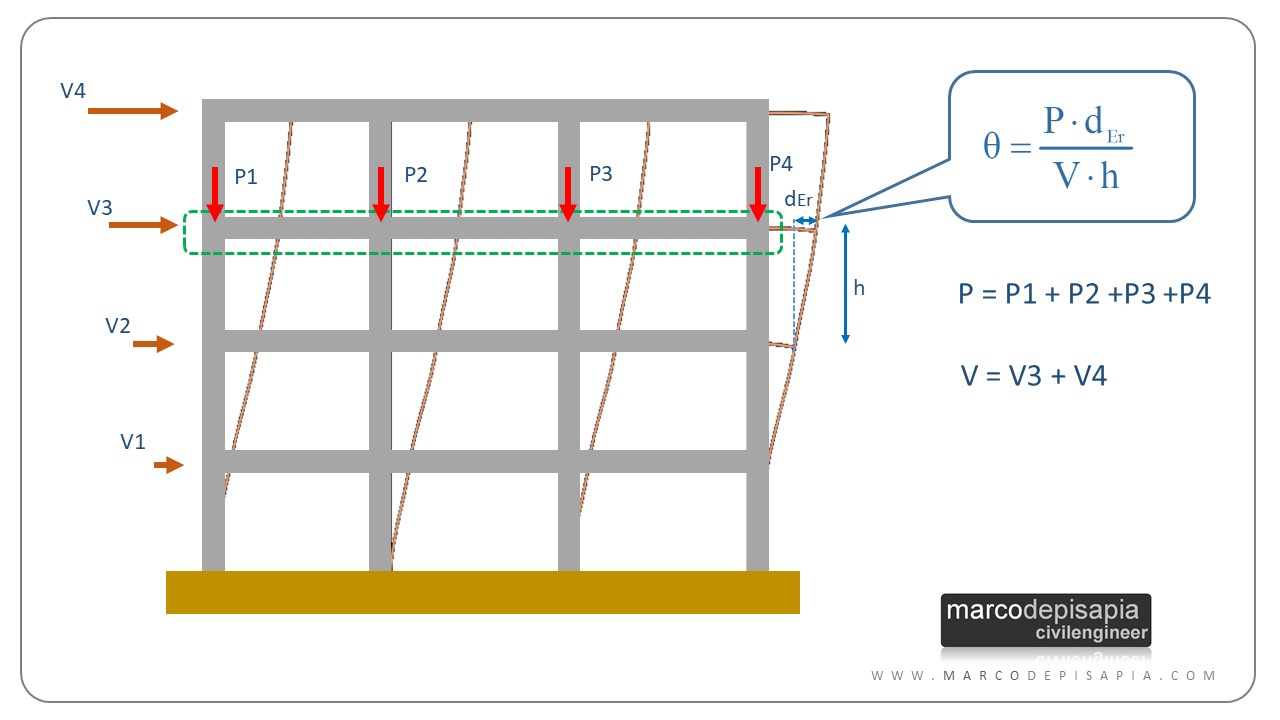
A seconda del valore assunto dal parametro θ si possono trascurare oppure no gli effetti delle non linearità geometriche. In particolare gli effetti delle non linearità geometriche:

• possono essere trascurati, quando θ è minore di 0,1;
• possono essere presi in conto quando θ è compreso tra 0,1 e 0,2; l’incremento degli effetti dell’azione sismica orizzontale si ottiene tramite un fattore pari a 1/(1-θ). Ciò equivale ad un incremento delle sollecitazioni dovute all’azione sismica compreso fra l’11% e il 25%.
• devono essere valutati attraverso un’analisi non lineare, quando θ è compreso tra 0,2 e 0,3.
• Il fattore θ non può comunque superare il valore 0,3. In tal caso bisognerà riprogettare la struttura in quanto troppo deformabile per le azioni orizzontali. Bisognerà quindi dimensionare le sezioni degli elementi strutturali in modo tale da renderla più rigida lateralmente.

Da dove deriva il parametro θ [Math Alert]

Per capire da dove deriva il parametro θ e l’effetto di amplificazione degli effetti dell’azione sismica valutato tramite il fattore 1/(1-θ) si può fare riferimento ad un telaio semplice caricato da due forze verticali e da una forza orizzontale.

In questa sezione del post ti mostrerò alcuni passaggi matematici per mostrarti da dove deriva l’incremento delle sollecitazioni in funzione del parametro θ. Ho cercato di rendere i passaggi matematici in modo chiaro e semplice. Se non sei interessato a questi passaggi un po’ più tecnici puoi saltare direttamente al paragrafo successivo.

---

A causa dello spostamento orizzontale del traverso per effetto della forza F0, le azioni assiali nei pilastri (N1 e N2), consideriate agenti nella configurazione deformata, daranno vita ad un incremento dello spostamento orizzontale e delle sollecitazioni.

δ0 = F0 / K     [spostamento orizzontale per effetto della forza F0; K = rigidezza laterale del telaio]

---

Prima iterazione: calcolo di δ1

M1 = N ⋅ δ0     [momento del secondo ordine calcolato sulla configurazione deformata; N = N1+N2]

F1 = M1 / H =  N ⋅ δ0 / H     [taglio fittizio provocato dal momento del secondo ordine; H = altezza del pilastro]

δ1 = F1 / K = [N / (H⋅K)] ⋅ δ0     [spostamento del secondo ordine generato dal taglio fittizio]

---

Seconda iterazione: calcolo di δ2

M2 = N ⋅ δ1    [momento del secondo ordine, seconda iterazione]

F2 = M2 / H =  N ⋅ δ1 / H    [taglio fittizio provocato dal momento del secondo ordine]

δ2 = F2 / K = [N / (H⋅K)] ⋅ δ1      [spostamento generato dal taglio fittizio]

Sostituisco il δ1 calcolato nell’iterazione precedente:

δ2 = [N / (H⋅K)] ⋅ [N / (H⋅K)] ⋅ δ0 = [N / (H⋅K)]^2 ⋅ δ0

---

Terza iterazione: calcolo di δ3

δ3 =  [N / (H⋅K)]^3 ⋅ δ0

---

Spostamento orizzontale per effetti del secondo ordine

δ = δ0 + δ1 + δ2 + δ3….     [somma degli spostamenti di ciascuna iterazione]

δ = δ0 + [N / (H⋅K)] ⋅ δ0 +  [N / (H⋅K)]^2 ⋅ δ0 + [N / (H⋅K)]^3 ⋅ δ0 ….

δ = δ0 ⋅  1/ (1 – [N / (H⋅K)])       (Somma di una serie geometrica di ragione [N / (H⋅K)] )

δ = δ0 ⋅  1/ (1 – [N ⋅ δ0/ (H⋅F0)])      [sostituisco K = F0 / δ0 ]

Si ritrova in tal modo il parametro θ che sarà pari a [N ⋅ δ0/ (H⋅F0)] così come prescritto dalle NTC2018. L’incremento dello spostamento (e di conseguenza delle sollecitazioni) ottenuto per il telaio semplice sarà pari a 1/ (1 – [N ⋅ δ0/ (H⋅F0)]) che coincide con il fattore di incremento proposto dalla Normativa e pari a 1/(1-θ).

Conclusioni

Nella maggior parte dei casi gli effetti del secondo ordine per strutture ordinarie sono trascurabili, in quanto il parametro θ risulterà essere inferiore a 0.10. E’ comunque sempre consigliabile controllare il valore assunto da questo parametro dopo aver completato l’analisi sismica della struttura per accertarsi che tali effetti siano effettivamente trascurabili.

Per strutture particolarmente snelle e deformabili lateralmente potrebbe essere necessario tener conto degli effetti del secondo ordine amplificando le sollecitazioni derivanti dall’azione sismica per un fattore di amplificazione calcolato in funzione del parametro θ, come riportato sopra.

L’unico caso in cui dovrai eseguire un’analisi del secondo ordine sarà quando il parametro θ è compreso fra 0.2 e 0.3. In tal caso dovrai eseguire un‘analisi P-Δ. E’ la stessa analisi eseguita per la struttura più alta del mondo, il Burj Khalifa con i suoi 828 metri di altezza (te ne ho parlato in questo post).

Il post di oggi finisce qui. Spero ti sia stato utile. Se è la prima volta che visiti questo blog, iscriviti alla newsletter per non perdere nessun nuovo articolo. Riceverai l’ultimo articolo pubblicato direttamente nella tua casella email. Ad iscrizione completata riceverai subito in omaggio quattro applicazioni utili per il calcolo strutturale. Non perdertele. Compila i campi qui sotto per completare l’iscrizione:

Se l’articolo ti è piaciuto, condividilo con i tuoi colleghi e amici cliccando sui tasti di condivisione Facebook o Linkedin qui sotto.

Al prossimo post.

Marco.