Quando la deformabilità di una struttura è eccessiva, bisognerà portare in conto gli effetti del secondo ordine. Te ne ho parlato nel post della settimana scorsa. Nel nuovo articolo di oggi voglio mostrarti un esempio numerico riguardante l’analisi di una struttura multipiano a tre livelli. Vedremo un confronto fra i risultati dell’analisi sismica eseguita nei seguenti tre casi:
- effetti del secondo ordine trascurabili;
- effetti del secondo ordine non trascurabili e portati in conto in modo semplificato amplificando le sollecitazioni sismiche;
- effetti del secondo ordine non trascurabili e calcolati attraverso un’analisi non-lineare (P-Delta).

All’interno dell’articolo potrai scaricare una risorsa gratuita interattiva che simula le non linearità geometriche per un sistema strutturale semplice. Non perderti il nuovo articolo di oggi e la risorsa allegata. Buona lettura.
Le non linearità geometriche: cosa sono [scarica la risorsa]
L’analisi strutturale può portare in conto due tipi di non linearità:
- non linearità del materiale: il materiale presenta un legame costitutivo non-lineare, entrando in campo plastico una volta superato il limite elastico;
- le non linearità geometriche: viene abbandonata l’ipotesi di piccoli spostamenti; le deformazioni del primo ordine producono uno spostamento non trascurabile del punto di applicazione del carico; ne consegue che dovranno essere ricalcolate le sollecitazioni e gli spostamenti del modello considerando i carichi applicati alla configurazione deformata, seguendo una procedura iterativa.
Per mostrarti l’effetto delle non linearità geometriche in un’analisi del secondo ordine ho creato per te una nuova risorsa gratuita. La risorsa riproduce un sistema formato da un’asta incernierata ad un’estremità, vincolata con una molla rotazionale in corrispondenza dell’appoggio. Cliccando sui tasti freccia potrai incrementare la forza verticale applicata e visualizzare gli spostamenti del sistema. All’aumentare dell’intensità della forza agente, aumenterà la rotazione dell’asta. Ma a causa degli effetti del secondo ordine, il legame forza-spostamento non sarà lineare (non linearità geometriche).
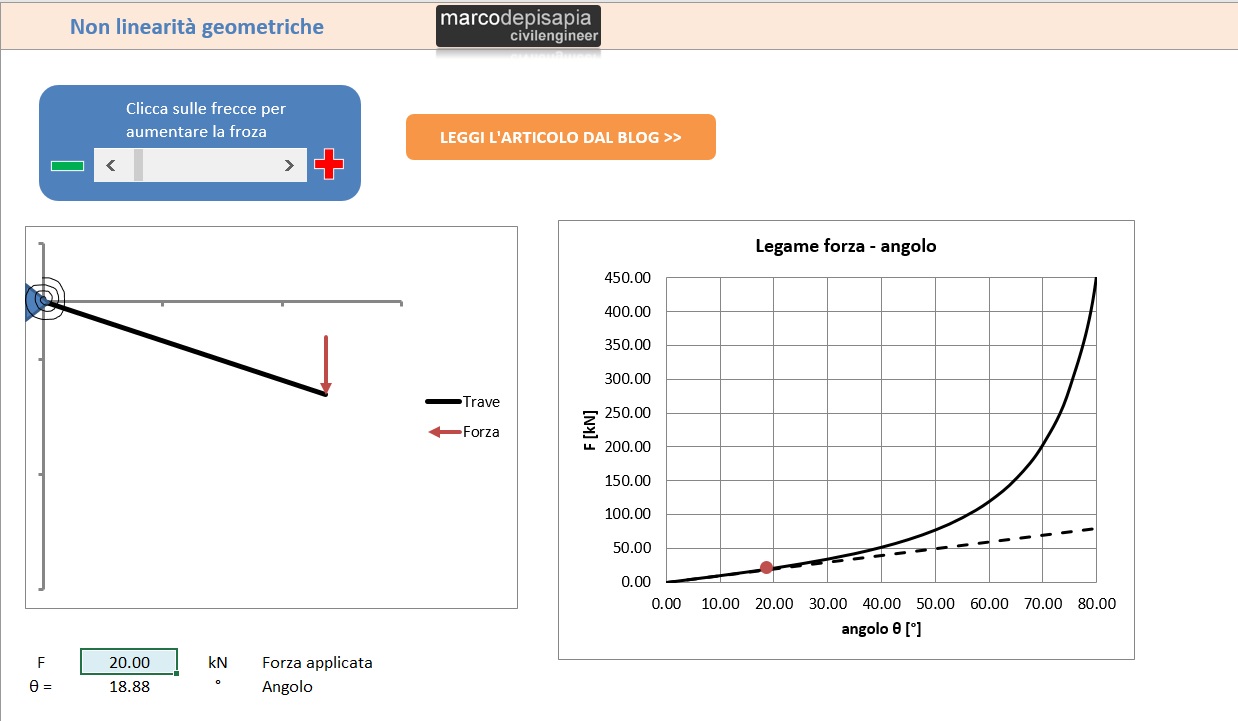
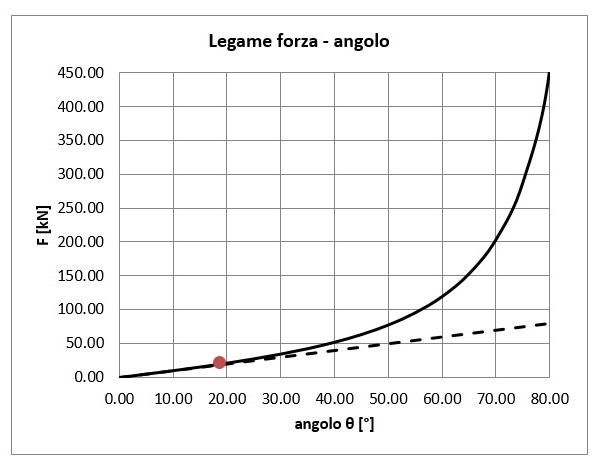
Il legame forza-spostamento (in questo caso lo spostamento è misurato mediante l’angolo di rotazione dell’asta) è lineare fino ad un valore modesto della forza F. Per valori modesti della forza agente valgono le ipotesi di piccoli spostamenti. Man mano che la rotazione dell’asta aumenta, il punto di applicazione del carico si sposta e il braccio della forza si riduce. Per ottenere incrementi costanti dell’angolo di rotazione dell’asta, occorreranno incrementi di forza sempre maggiori. Il legame forza-spostamento non segue un andamento lineare, ma esponenziale, dando vita alle cosiddette non-linearità geometriche.
Scarica la risorsa gratuita: compila i campi qui sotto
Inserisci il tuo nome e indirizzo email. Riceverai all’istante la risorsa nella tua casella email.

Un caso studio: struttura multipiano a tre livelli
Nel seguito del post ti mostro un esempio numerico. Si tratta dell’analisi di un modello strutturale tridimensionale a tre livelli. I pilastri hanno sezione 40×40, le travi sezioni 30×50. L’altezza di interpiano del secondo impalcato è stata modificata per ciascun esempio al fine di ottenere un valore del fattore θ via via crescente, facendo crescere l’influenza degli effetti del secondo ordine. Di seguito i tre casi analizzati:
- fattore θ minore di 0.10 – gli effetti del secondo ordine sono trascurabili;
- fattore θ fra 0.10 e 0.20 – bisogna amplificare le sollecitazioni sismiche del fattore 1/(1-θ);
- Fattore θ fra 0.20 e 0.30 – bisogna eseguire un’analisi del secondo ordine (P-Delta)
Esempio 1: θ minore di 0.10 – effetti del secondo ordine trascurabili
In questo esempio il valore massimo del fattore θ è pari a 0.003. Siamo davvero lontani dal limite di 0.10. Di conseguenza gli effetti delle non linearità geometriche sono trascurabili.

Esempio 2: θ compreso fra 0.10 e 0.20 – effetti del secondo ordine non trascurabili
Nel secondo esempio il modello è stato modificato per aumentare l’effetto delle non linearità geometriche. L’altezza di interpiano del secondo impalcato è stata notevolmente aumentata. Il risultato ottenuto è un valore di θ pari a 0.13. In tal caso le sollecitazioni sismiche saranno amplificate del fattore 1/(1-θ) = 1/(1-0.13) = 1.15 a cui corrisponde un incremento del 15%.

Esempio 3: θ compreso fra 0.20 e 0.30 – L’analisi P-Delta per gli effetti del secondo ordine
Nell’ultimo esempio è stata ulteriormente incrementata l’altezza di interpiano del secondo impalcato. In quest’ultimo caso il fattore θ raggiunge un valore pari 0.24. In tal caso per portare in conto gli effetti del secondo ordine, non è possibile utilizzare il fattore di amplificazione 1/(1-θ), ma bisognerà eseguire un’analisi non-lineare, ovvero un’analisi P-Delta che porti in conto le non linearità geometriche. Dai risultati ottenuti dall’Analisi P-Delta si è avuto un incremento del 22% delle sollecitazioni del secondo ordine rispetto a quelle del primo ordine.
Conclusioni
Dagli esempi mostrati hai potuto vedere che gli effetti del secondo ordine sono solitamente trascurabili per strutture ordinarie. Per strutture con particolari altezze di interpiano gli effetti delle non linearità geometriche diventano più consistenti. Ma fino ad un valore del fattore θ pari a 0.20, la Normativa Tecnica dà la possibilità di considerarle in maniera semplificata amplificando le sollecitazioni sismiche, senza eseguire analisi non-lineari. Quando invece il fattore θ raggiunge un valore maggiore di 0.20, allora dovrai obbligatoriamente eseguire un’analisi non-lineare.
L’articolo di oggi finisce qui. Prima di salutarci ti ricordo che è di nuovo disponibile Calculation WEB, il servizio di calcolo strutturale online dedicato in esclusiva agli iscritti del blog. I posti disponibili sono soltanto tre ed un posto è stato già occupato. Il servizio verrà sospeso al raggiungimento del numero massimo di posti. Per richiedere un preventivo clicca sul link di seguito:
Richiedi il tuo preventivo per Calculation WEB (clicca qui)
Se hai trovato utile il post di oggi e vuoi suggerirlo ai tuoi amici e colleghi su Linkedin o Facebook, clicca sui tasti di condivisione qui sotto. Grazie mille 🙂
Al prossimo post.
Marco.
