Rigidezza assiale pilastri: ecco come correggerla

Nel post di oggi ti spiego perché considerare la deformabilità assiale dei pilastri può portarti a sovrastimare le sollecitazioni nelle travi, soprattutto quelle degli ultimi piani. So che a primo impatto può sembrarti strano, ma ti assicuro che tra un po’ ti sarà tutto più chiaro. Alla fine del post ti suggerisco un metodo pratico per evitare questo errore e correggerlo.

Qualche tempo fa, quando non era ancora disponibile la potenza di calcolo che abbiamo a disposizione oggi, i telai piani venivano risolti con metodi numerici, per esempio metodi di rilassamento come il Metodo di Hardy Cross.

Questi metodi adottavano delle ipotesi semplificative per rendere la risoluzione degli schemi strutturali più agevole. Le ipotesi semplificative principali erano le seguenti:

• infinita rigidezza assiale delle aste;
• trascurabilità della deformabilità tagliante.

In pratica le aste venivano ipotizzate deformabili soltanto flessionalmente. L’errore che si commetteva era trascurabile, in quanto gli spostamenti dovuti alla deformabilità flessionale sono molto più elevati rispetto a quelli dovuti alla deformabilità assiale.

Con il diffondersi dei computer e i modelli di calcolo diventano sempre più sofisticati. Per un moderno codice di calcolo oggi è scontato considerare:

• la deformabilità assiale delle aste;
• la deformabilità tagliante;
• la deformabilità flessionale.

Alcuni software considerano anche l’eccentricità fra il centro di taglio e l’asse baricentrico dell’asta, altri considerano il non allineamento delle aste in corrispondenza dei nodi, dovuto alla rastremazione dei pilastri ai diversi livelli.

Insomma tutto porterebbe a credere che modelli così sofisticati riproducano meglio il comportamento reale di una struttura. Invece non sempre è così. Ci crederesti se ti dicessi che sotto alcuni aspetti i modelli semplificati che si utilizzavano in passato erano più accurati di quelli attuali? In particolare mi riferisco ad un effetto connesso con la rigidezza assiale dei pilastri. 

Considerare le aste deformabili assialmente utilizzando un software di calcolo ti porterà a commettere un errore, soprattutto ai piani alti e soprattutto per edifici con un elevato numero di piani. Ti spiego di seguito perché.

La causa dell’errore: una struttura si costruisce un piano per volta

La causa dell’errore nella valutazione dei momenti sollecitanti nelle travi, soprattutto in quelle degli ultimi piani, è dovuto alla differenza di cedimenti fra le diverse pilastrate: quelle di estremità e quelle centrali. L’origine dell’errore si può riassumere in una singola frase: una struttura viene costruita un piano alla volta.

Mi spiego meglio. In un software di calcolo creiamo il modello della nostra struttura e finché non lanciamo il calcolo questo modello resta indeformato. Poi clicchiamo un bottoncino e di colpo alla nostra struttura vengono applicati i carichi agenti e calcolate le deformazioni e le sollecitazioni.

Ma non è affatto questo che accade nella realtà. Una struttura viene costruita un piano alla volta e già durante le fasi di costruzione è presente il carico dovuto al peso proprio della struttura. In particolar modo per le strutture in cemento armato, in cui il peso degli impalcati rappresenta un’aliquota considerevole del carico totale. La struttura inizia a deformarsi già durante le fasi di costruzioni e man mano che la costruzione procede, gli impalcati di piano si adattano a queste deformazioni durante la maturazione del calcestruzzo. Le sollecitazioni che sorgono nelle travi di impalcato si avranno solo per effetto del peso degli impalcati superiori una volta che la maturazione del calcestruzzo sarà terminata.

I software di calcolo riproducono una situazione irrealizzabile nella realtà. Ciò che succede in un software di calcolo equivale a “spegnere” la forza di gravità, costruire interamente una struttura e poi “riaccendere” di colpo la gravità, applicando il carico del peso proprio. Cosa ovviamente impossibile.

Un esempio pratico

Voglio mostrarti con un esempio pratico la differenza in termini di deformazioni assiali dei pilastri fra una struttura reale e una struttura modellata in un software di calcolo. Nelle immagini che seguono ti mostro la differenza fra queste due situazioni. Le deformazioni assiali dei pilastri sono state notevolmente amplificate per mettere in risalto il fenomeno.

Negli esempi che seguono ciascun pilastro è diviso in cinque conci. Ipotizzeremo che in seguito all’applicazione del peso proprio dell’impalcato, il pilastro centrale si comprimerà accorciandosi di un concio, i pilastri laterali invece di metà concio, essendo lo sforzo normale agente sui pilastri laterali pari alla metà rispetto a quello centrale. Di seguito puoi vedere cosa accade alla realizzazione di ciascun impalcato per una struttura nella realtà.

Realizzazione del primo impalcato

Dopo la maturazione dei pilastri viene gettato il primo impalcato. Per effetto del peso proprio del solaio, il pilastro centrale si deformerà accorciandosi di un concio, quelli laterali si accorceranno di metà concio. La differenza di cedimenti fra la pilastrata centrale e quelle laterali è di metà concio, come indicato nell’immagine sotto.

Realizzazione del secondo impalcato

Si passa poi alla realizzazione del secondo impalato. Per raggiungere la quota del secondo impalcato, i pilastri del secondo ordine (di colore rosso in figura) dovranno essere più lunghi per compensare l’accorciamento delle pilastrate sottostanti. Il pilastro centrale sarà quindi lungo 6 conci invece di 5, mentre quelli laterali saranno lunghi 5,5 conci.

In seguito alla realizzazione del secondo impalcato, la pilastrata centrale si accorcerà di un concio al primo livello e di un concio al secondo livello. Quelle laterali invece di metà concio per ciascun livello. Il cedimento differenziale fra le pilastrate laterali e centrale è di un concio.

Realizzazione del terzo impalcato

Lo stesso procedimento si ripete per ogni nuovo impalcato. Stavolta i pilastri del terzo ordine saranno lunghi 7 conci invece di 5, mentre quelli laterali 6 conci invece di 5. Ciò è necessario per raggiungere la quota del terzo impalcato, compensando le deformazioni assiali delle pilastrate sottostanti. Alla realizzazione del terzo impalcato nuovamente le pilastrate centrali e laterali si accorceranno rispettivamente di un concio e metà concio per ogni livello. I cedimenti differenziali sono indicati in figura.

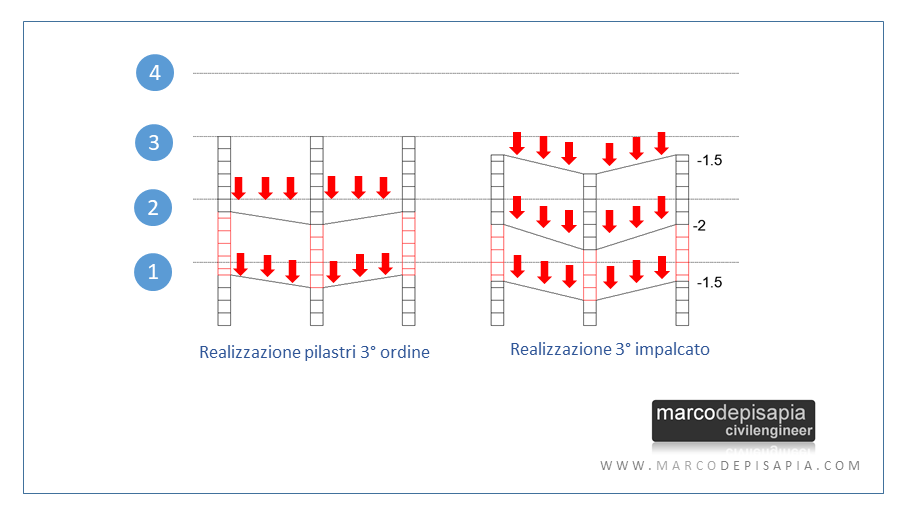
Realizzazione del quarto impalcato

Ultimo step. Realizzazione del quarto impalcato. Le pilastrate del quarto ordine saranno lunghe 8 conci (la centrale) e 6.5 quelle laterali per compensare gli accorciamenti delle pilastrate sottostanti e raggiungere la quota del quarto livello. In seguito alla realizzazione del quarto impalcato, le pilastrate centrali si deformeranno come nei casi precedenti.

I cedimenti differenziali finali espressi in conci fra la pilastrata centrale e le laterali sono:

• -2.0 al primo ordine
• -3.0 al secondo ordine
• -3.0 al terzo ordine;
• -2.0 al quarto ordine.

Questo è quanto accade per una struttura reale durante una normale fase di costruzione. Vediamo di seguito invece cosa accade in un software di calcolo.

Cosa accade in un modello di calcolo

A differenza dei casi precedenti, in un software di calcolo le cose funzionano diversamente. E’ come se la struttura venisse realizzata per intero, e solo a fine costruzione agissero di colpo i carichi verticali dovuti al peso proprio. Di conseguenza per effetto dello sforzo normale agente nei pilastri, si avranno gli accorciamenti nelle pilastrate indicati in figura. 

Come puoi vedere i cedimenti differenziali finali fra le pilastrate centrali e le laterali sono:

• -2.0 al primo ordine;
• -3.5 al secondo ordine;
• -4.5 al terzo ordine;
• -5.0 al quarto ordine.

Se li confrontiamo con quelli del caso reale si nota la differenza:

• primo ordine: stesso cedimento differenziale per i due casi;
• secondo ordine: -3.5 invece di -3.0 [+17%]
• terzo ordine: -4.5 invece di -3.0 [+50%]
• quarto ordine: -5.0 invece di -2.0 [+150%]

Come puoi vedere dai risultati ottenuti, man mano che si sale di livello, l’incremento di cedimento differenziale aumenta arrivando al 150% per i pilastri del quarto ordine. Questo incremento di cedimenti differenziali genera un momento sollecitante aggiuntivo nelle travi dei piani alti che nella realtà non esiste. Pertanto si commetterà un errore considerando la deformabilità assiale dei pilastri, soprattutto per edifici con un elevato numero di piani. 

La presenza del suolo alla Winkler

Lo stesso effetto dovuto alla deformabilità assiale dei pilastri è causato dalla presenza del suolo alla Winkler nel modello di calcolo. Nell’esempio precedente come hai potuto vedere la base dei pilastri non subiva spostamenti, nell’ipotesi di un incastro alla base. In realtà con il procedere delle fasi di costruzione della struttura, oltre alla deformabilità assiale dei pilastri entrano in gioco anche i cedimenti del terreno. Se abbiamo modellato il suolo elastico alla Winkler l’effetto di amplificazione delle sollecitazioni nelle travi sarà accentuato rispetto al caso della struttura incastrata alla base.

I terreni si possono didivdere in due categorie:

• terreni incoerenti (ghiaie e sabbie)
• terreni coerenti (argille e limi)

Per i primi il cedimento è praticamente istantaneo, la struttura si assesta in presenza di questi cedimenti man mano che la costruzione avanza.

Per i secondi invece il cedimento è composto da due aliquote: un cedimento istantaneo che si verifica all’atto dell’applicazione del carico; un cedimento di consolidazione che si verifica in tempi molto lunghi, anche nell’arco di anni. La struttura si adeguerà quindi ai cedimenti di consolidazione per effetto del fluage.

In entrambi i casi i cedimenti calcolati saranno ben diversi da quelli che si avrebbero nella realtà, soprattutto per le membrature dell’ultimo piano.

La soluzione al problema

Qual è la soluzione a questo problema? Per ovviare a questo errore nella valutazione delle sollecitazioni ai piani alti della struttura c’è un escamotage che puoi utilizzare. La soluzione consiste nell’amplificare la rigidezza assiale dei pilastri nel calcolo delle combinazioni non sismiche, per avvicinarti alle reali sollecitazioni che si verificano nella realtà. Il coefficiente di amplificazione può essere assunto pari a:

• 10 volte il numero di piani per strutture intelaiate prive di pareti; per esempio per una struttura di 10 piani, la rigidezza assiale sarà amplificata di 100 volte;
• pari a 10 per strutture con pareti irrigidenti;

L’amplificazione della rigidezza assiale va utilizzata per la valutazione delle sollecitazioni in combinazioni non-sismiche, quindi nei riguardi dei soli carichi verticali agenti. Nel caso di combinazioni sismiche la rigidezza assiale invece non va amplificata.

Per tenere in conto gli effetti dei cedimenti del terreno, per combinazioni non sismiche conviene calcolare la struttura applicando dei vincoli ad incastro alla base dei pilastri. Successivamente bisognerà calcolare la fondazione applicando le reazioni vincolari degli incastri alla struttura di fondazione.

Il post di oggi finisce qui. La prossima volta che ti trovi ad eseguire un calcolo strutturale, soprattutto per strutture molto alte, ricordati dell’escamotage di cui ti ho parlato nell’articolo di oggi.

Valgono le solite regole: se hai trovato utile l’articolo puoi suggerirlo ai tuoi amici su Facebook o ai tuoi colleghi su LinkedIn cliccando sui tasti di condivisione social che trovi in fondo alla pagina.

Al prossimo articolo.

Marco.