Se vuoi memorizzare in maniera veloce ed efficace formule matematiche ti consiglio di leggere quest’articolo. Che tu sia uno studente o un professionista di un settore tecnico (ingegnere, architetto, geometra etc.), ti troverai continuamente ad avere a che fare con formule matematiche più o meno complesse. Le Normative tecniche sono in continua evoluzione. Ad ogni nuovo aggiornamento le prescrizioni contenute diventano sempre più accurate e di pari passo le formule matematiche che propongono sempre più complesse.

E’ molto utile per un tecnico, così come per uno studente di materie scientifiche, comprendere ciò che si nasconde dietro una formula. Capire il comportamento, il fenomeno fisico o l’andamento che una formula vuole riprodurre ci aiuterà a memorizzarla e ad evitare errori.
Come capire e memorizzare le formule matematiche
Per memorizzare e comprendere al meglio una formula matematica, puoi seguire questi quattro semplici passi:
- osserva la formula attentamente ed elenca tutti i parametri da cui dipende, magari scrivendoli su un foglio.
- implementa la formula in un foglio elettronico, impostando delle celle per tutti i parametri di input e una cella che calcoli il risultato finale (puoi usare questi 5 trucchi per creare un foglio elettronico efficace)
- inizia a sperimentare, ovvero fai variare i valori di un parametro per volta per vedere come cambia il risultato.
- crea un grafico che metta in relazione un parametro con il risultato finale, in modo da poter studiare l’andamento della funzione al variare di quel singolo parametro.
Usando questi semplici consigli magari perderai un pò di tempo in più, ma avrai dei risultati notevoli:
- la formula e il modo in cui i suoi parametri interagiscono fra loro ti resteranno impressi nella memoria e sarà più difficile dimenticarli, anche a distanza di tempo;
- avrai più padronanza del risultato ottenuto e se avrai bisogno di ottenere un risultato diverso saprai su quali parametri agire;
- ti ritroverai un foglio elettronico già pronto che potrai utilizzare per i tuoi calcoli o per validare i risultati di un software di calcolo commerciale.
Una piccola precisazione: non è importante memorizzare perfettamente una formula matematica, perché nel giro di pochi giorni probabilmente non la ricorderai più, o la ricorderai in una forma sbagliata. In entrambi i casi avrai sprecato il tuo tempo. Ciò che è importante è ricordare da quali parametri questa formula dipende e come la variazione di ciascun parametro influisce sul risultato finale. Ricordare la forma esatta di una formula è una diretta conseguenza dei passi descritti in precedenza.
Se poi vuoi davvero memorizzare una formula per non scordarla mai più, magari perché a breve devi sostenere un esame universitario o l’esame finale di un corso di specializzazione, ciò che devi fare è inventarti una “storiella”. Ti potrà sembrare strano, ma se riesci a trovare una storiella, magari anche buffa, che ti aiuti a memorizzare cosa fa la formula e da quali parametri dipende, sta sicuro che la formula che stai imparando non la scorderai mai più.
Sei scettico? Ti riporto di seguito un esempio concreto. Continua a leggere.
L’esempio che voglio farti riguarda la formula della serie di Taylor. Sia che tu sia uno studente, sia che tu sia un professionista super esperto di complessi calcoli scommetto che non ricordi perfettamente cosa fa in pratica la serie di Taylor (a meno che tu non stia preparando in questi giorni l’esame di analisi ;-)). E’ a questo punto che entra in gioco la storiella buffa di cui ti parlavo.
Quando ero studente e mi trovai a dover imparare la serie di Taylor, per memorizzarla usai le tecniche che ti ho descritto sopra e una volta capito cosa faceva questa funzione e qual’era il suo scopo, mi inventai una storiella per ricordarlo.
La storiella del fabbro operoso
La serie di Taylor è come un possente fabbro, che lavora senza sosta per modellare e piegare, con i suoi colpi di martello, una spada sulla superficie curva di una botte. Ovviamente più colpi di martello il fabbro darà alla spada, meglio questa seguirà l’andamento curvo della superficie della botte. La variabile fondamentale è proprio il numero di colpi di martello. Con un solo colpo (un fabbro davvero pigro) la spada resterà quasi dritta, indeformata, non riuscirà a piegarsi in modo da seguire il percorso curvo. Con tre colpi di martello la spada inizierà a piegarsi, seguendo per un piccolo tratto la superficie curva della botte. Con sette colpi seguirà la superficie curva per un tratto più lungo e così via. Ovviamente per centinaia di colpi (un fabbro che lavora senza sosta) la spada si curverà seguendo perfettamente la superficie della botte. Il fabbro avrà raggiunto il suo scopo!
E’ proprio ciò che fa la Serie di Taylor. La botte rappresenta la funzione che si vuole approssimare con la serie di Taylor, il numero di colpi è il numero di termini della serie di Taylor che consideriamo, ovvero il parametro n che per n che tende all’infinito (infiniti colpi di martello) farà combaciare perfettamente la serie di Taylor con la funzione che si vuole approssimare.
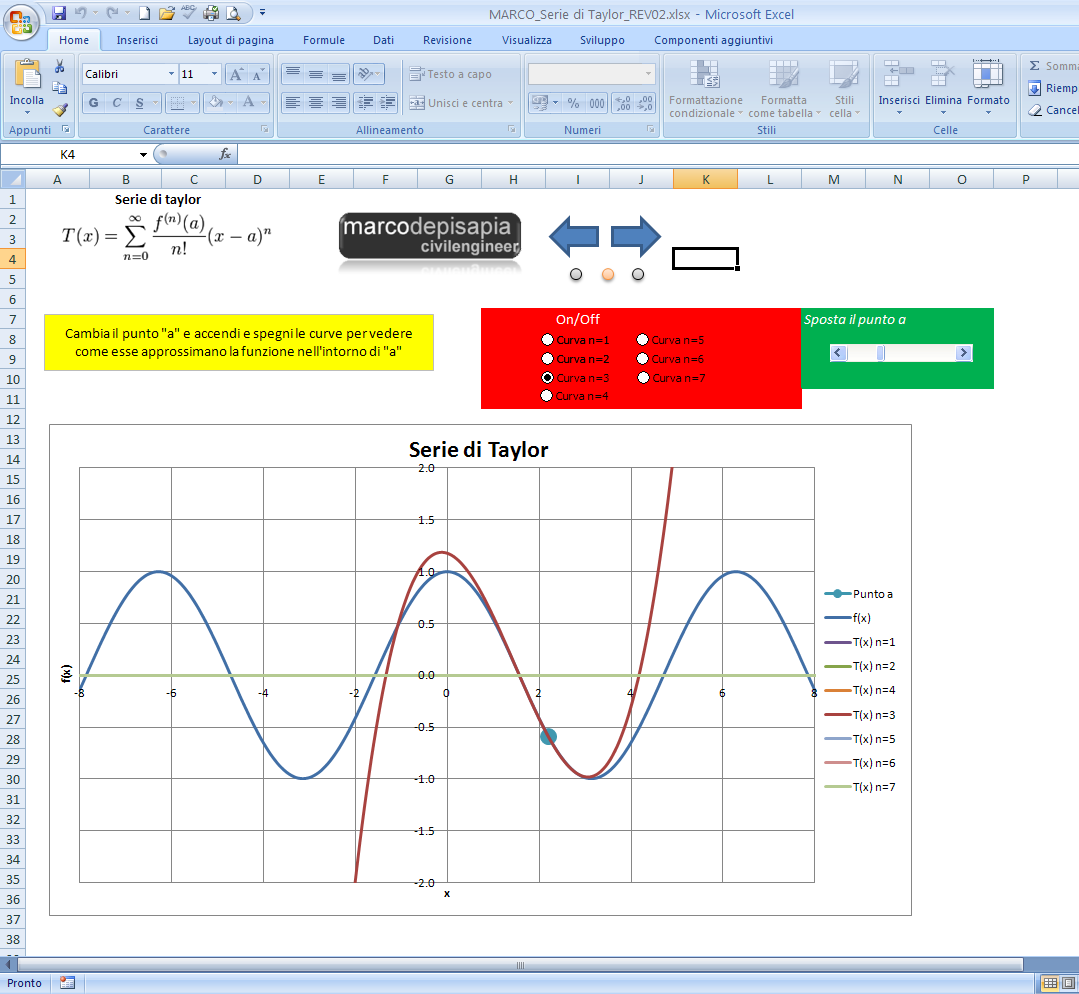
Per rendere più chiaro quello che fa la serie di Taylor, questa settimana allego all’articolo una nuova risorsa. Un foglio elettronico nel quale potrai cambiare il numero di termini della serie (i colpi di martello) e vedere in un grafico cosa fa la Serie di Taylor.
Scarica la risorsa gratuita
Se sei iscritto alla newsletter di marcodepisapia.com hai ricevuto il link per il download della risorsa nell’email ricevuta al momento della pubblicazione dell’articolo. Se non sei ancora iscritto o non trovi la vecchia email clicca sul pulsante qui sotto e completa l’iscrizione. L’iscrizione è gratuita e ti consentirà di scaricare la risorsa in pochi secondi, insieme a tutte le altre risorse che distribuirò in futuro.

Immagino che difficilmente dimenticherai cosa fa la serie di Taylor, grazie ad una buffa storiella e ad un foglio elettronico nel quale ti suggerisco di provare a cambiare i parametri per vedere cosa succede. Mi raccomando, non far stancare troppo il nostro fabbro 😉
Se hai trovato utile la risorsa e questo articolo fammi sapere che ne pensi nei commenti.
Alla prossima settimana.
