L’oscillatore semplice è un sistema vibrante ad un solo grado di libertà schematizzato mediante una massa, una molla e uno smorzatore. Questo semplice sistema fisico è alla base dell’analisi dinamica delle costruzioni in zona sismica. Conoscere le proprietà di un oscillatore semplice e la sua risposta al variare dei parametri che lo caratterizzano e delle condizioni al contorno è una competenza fondamentale per un progettista strutturale.
In quest’articolo ti parlo delle proprietà principali di un oscillatore semplice e della risposta in termini di spostamento e accelerazione che si ottiene facendo variare le condizioni al contorno e le proprietà del sistema.
Per rendere più agevole la comprensione del sistema massa-molla-smorzatore, alla fine del post potrai scaricare una risorsa utility che riproduce, mediante animazioni interattive, la risposta in termini di spostamento nei tre casi seguenti:
- sistema libero (sistema massa-molla);
- sistema smorzato (sistema massa-molla-smorzatore);
- sistema smorzato e forzato (sistema massa-molla-smorzatore con applicazione di una forzante).
In fondo alla pagina troverai inoltre un video che riassume i contenuti di quest’articolo. Buona lettura.
Oscillatore semplice: come si schematizza con una massa, una molla e uno smorzatore
Nell’analisi sismica l’oscillatore semplice viene denominato anche SDOF system ovvero Single Degree Of Freedom system (sistema ad un solo grado di libertà) in quanto l’unico grado di libertà del sistema è lo spostamento nel piano orizzontale. Un oscillatore semplice può essere schematizzato in diversi modi. Ti elenco di seguito i tre schemi principali.
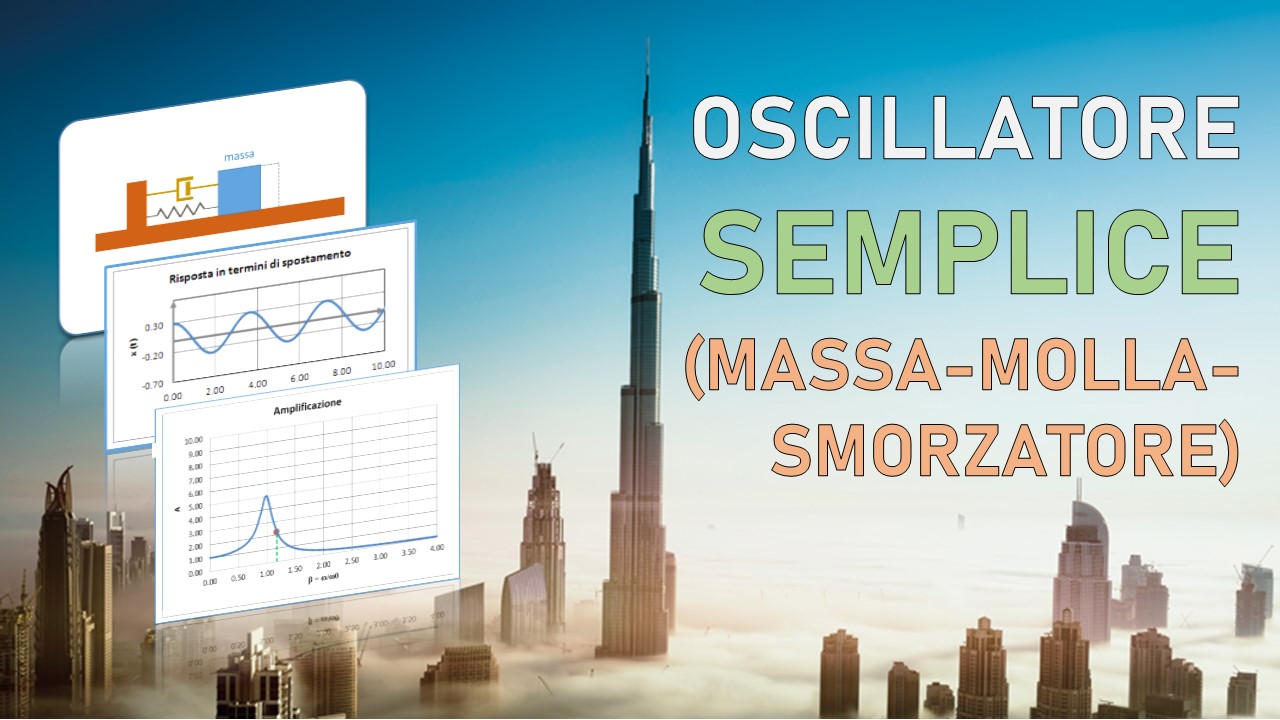
Sistema massa-molla-smorzatore
In questo schema l’oscillatore semplice è costituito da una massa libera di muoversi senza attrito su un piano orizzontale. La massa è collegata ad un piano verticale fisso mediante una molla e uno smorzatore disposti in parallelo.
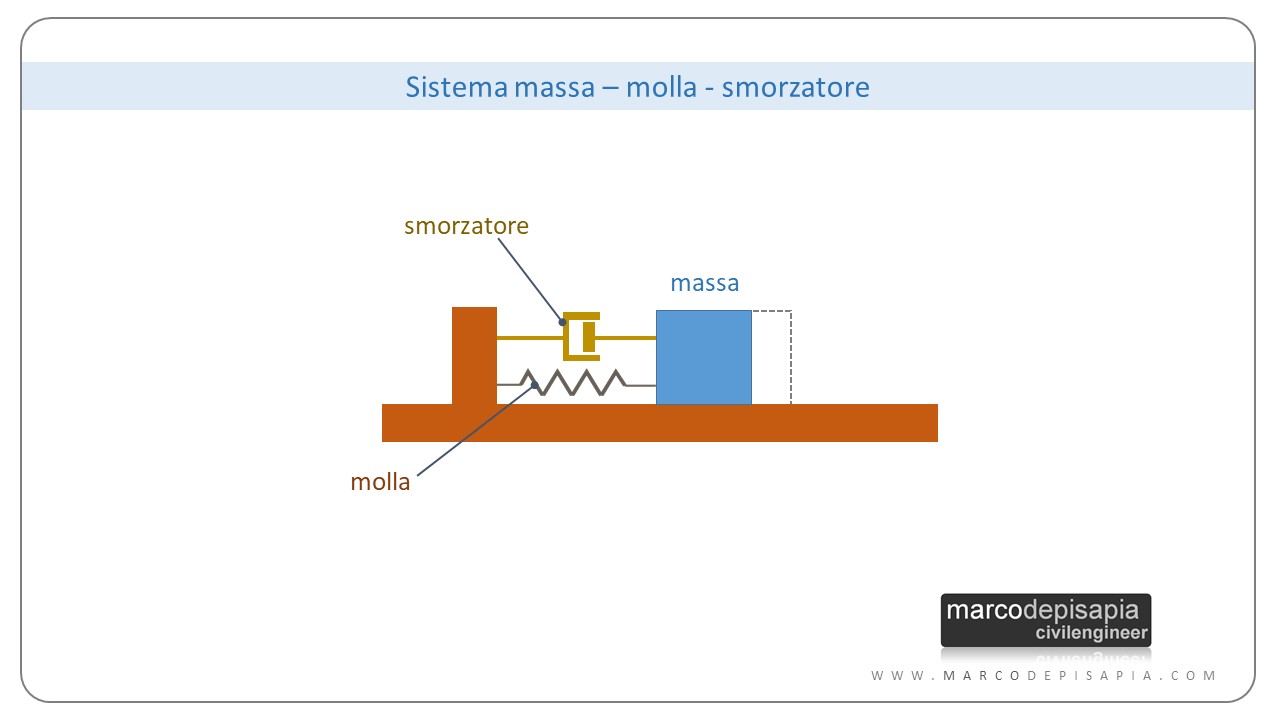
Telaio shear type
In questo schema l’oscillatore semplice è schematizzato mediante un telaio shear-type, ovvero un telaio in cui il traverso è infinitamente rigido e le colonne sono deformabili flessionalmente. In questo schema la molla è rappresentata dalle colonne dotate di una certa rigidezza traslante. Lo smorzatore invece può essere applicato al traverso e collegato al suolo, oppure si può attribuire la capacità di smorzamento alle colonne. La massa è concentrata nel traverso. Questo schema è molto utilizzato nelle trattazioni teoriche dell’analisi dinamica delle strutture.
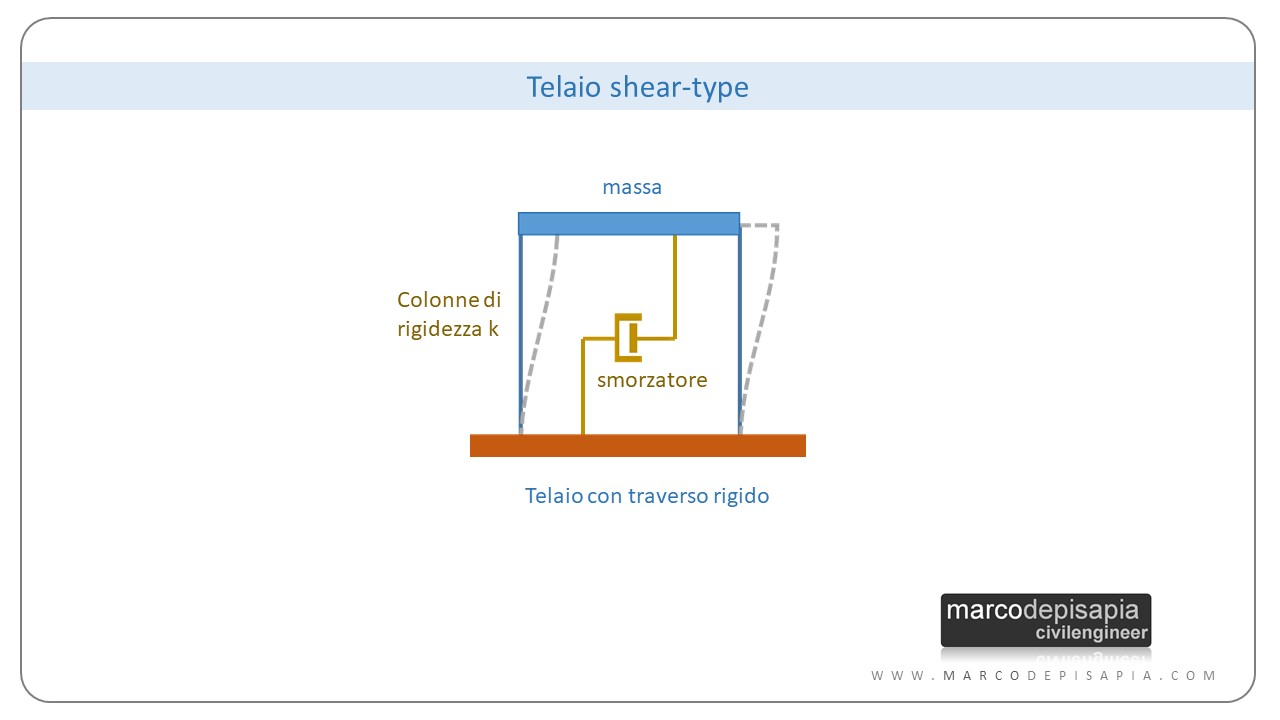
Struttura a lollipop
Il terzo schema con cui può essere rappresentato un oscillatore semplice è composto da una massa concentrata alla sommità di un’asta deformabile flessionalmente. In questo schema sia la molla che lo smorzatore sono proprietà intrinseche della colonna che avrà una data rigidezza traslante e una certa capacità di smorzamento.
Questo modello è molto utilizzato nell’analisi sismica per la definizione degli spettri di risposta e viene chiamato struttura a lollipop perché ricorda la forma di un lecca-lecca (appunto un lollipop in inglese), come definito nel testo Dynamics of Structures: Theory and Applications to Earthquake Engineering di Anil K. Chopra.
Oscillatore semplice: il periodo di vibrazione
Le caratteristiche di un oscillatore semplice sono le seguenti:
- la massa;
- la rigidezza;
- lo smorzamento viscoso
Lo smorzamento viscoso determina la progressiva riduzione dell’ampiezza delle oscillazioni nel tempo a causa delle proprietà viscose dei materiali.
Il periodo naturale di vibrazione, ovvero l’intervallo di tempo che la massa impiega per compiere un’oscillazione completa e tornare alla posizione di partenza, è una caratteristica che dipende solo dalla massa e rigidezza del sistema, non dallo smorzamento, e può essere calcolato mediante la seguente formula:
T = 2 ⋅ π √ (m / k)
- m = massa del sistema;
- k = rigidezza del sistema.
Periodo naturale di vibrazione
All’aumentare della massa, aumenterà il periodo di vibrazione, per rigidezza costante. Per massa costante, all’aumentare della rigidezza del sistema diminuirà il periodo di vibrazione.
Oscillatore semplice libero (sistema massa-molla)
L’oscillatore semplice libero è composto da una massa e una molla, in assenza di smorzamento. Nel modello a lollipop la colonna sarà dotata solo di rigidezza flessionale, senza alcuno smorzamento viscoso.
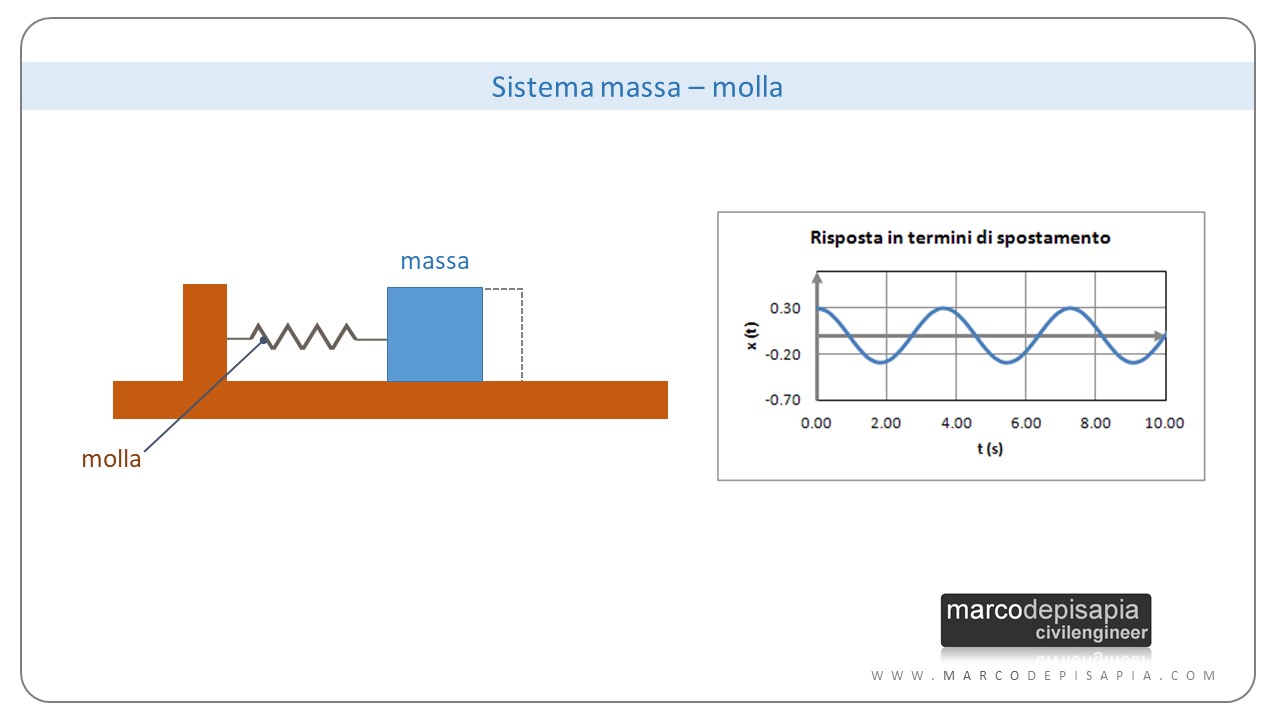
Spostando la massa dalla sua posizione di equilibrio, assegnando come condizione iniziale uno spostamento iniziale x0 al tempo t=0, oppure assegnando una velocità iniziale al tempo t=0, il sistema continuerà ad oscillare all’infinito intorno alla sua posizione di equilibrio, senza fermarsi mai. Si tratta di un comportamento idealizzato possibile solo nel caso in cui non ci sia nessuno smorzamento viscoso.
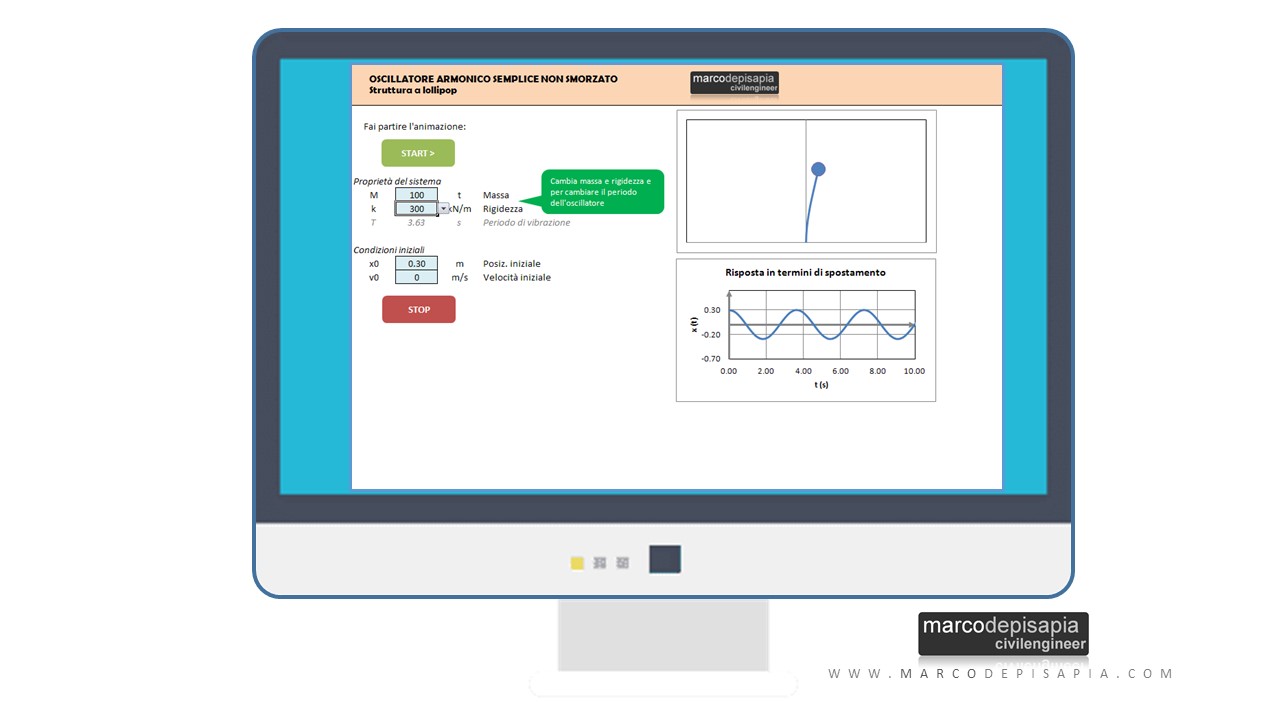
Oscillatore semplice libero: simulazione interattiva con la risorsa utility
All’interno della risorsa utility scaricabile alla fine del post potrai:
- assegnare le condizioni iniziali del sistema: posizione iniziale e velocità;
- far variare la massa e la rigidezza dell’oscillatore e osservare di conseguenza come varia il suo periodo;
- visualizzare il grafico della risposta in termini di spostamento in funzione del tempo;
- osservare l’animazione delle oscillazioni del modello a lollipop.
Oscillatore semplice smorzato (sistema massa-molla-smorzatore)
Un modello che riproduce in maniera più fedele la realtà è l’oscillatore semplice con smorzamento viscoso. La presenza dello smorzamento fa sì che l’ampiezza delle oscillazioni si riduca con il passare del tempo fino a riportare l’oscillatore alla sua posizione di equilibrio, annullando l’ampiezza delle oscillazioni.
E’ sufficiente un valore piccolo dello smorzamento (per esempio 0.05, ovvero il 5% dello smorzamento critico, vedremo tra poco cos’è) per osservare una significativa riduzione nell’ampiezza delle oscillazioni.
Nel caso di un oscillatore semplice smorzato possono presentarsi tre casi differenti a seconda del valore dello smorzamento:
- oscillatore sotto-smorzato: il valore dello smorzamento è maggiore o uguale a zero e minore di uno. Per un oscillatore sotto-smorzato si avranno delle oscillazioni intorno alla posizione di equilibrio prima di raggiungere lo stato di quiete;
- oscillatore con smorzamento critico: il valore dello smorzamento è pari a 1. In questo caso il sistema ritorna alla sua posizione di equilibrio senza oscillare e lo fa nel minor tempo possibile;
- oscillatore sovra-smorzato: il valore dello smorzamento è maggiore di 1. Anche in questo caso il sistema tornerà alla sua posizione di equilibrio senza oscillare, ma impiegherà un tempo superiore rispetto al caso di oscillatore con smorzamento critico.

Per l’oscillatore sotto-smorzato la presenza dello smorzamento non influisce in alcun modo sul periodo di vibrazione, ma solo sull’ampiezza delle oscillazioni. Questa proprietà spiega perché quando eseguiamo l’analisi modale di una struttura lo smorzamento non influisce sul periodo di vibrazione dei modi di vibrare.
Le costruzioni presentano in genere un valore dello smorzamento approssimativamente pari al 5%, sono quindi dei sistemi vibranti sotto-smorzati.
Oscillatore semplice smorzato: simulazione interattiva con la risorsa utility
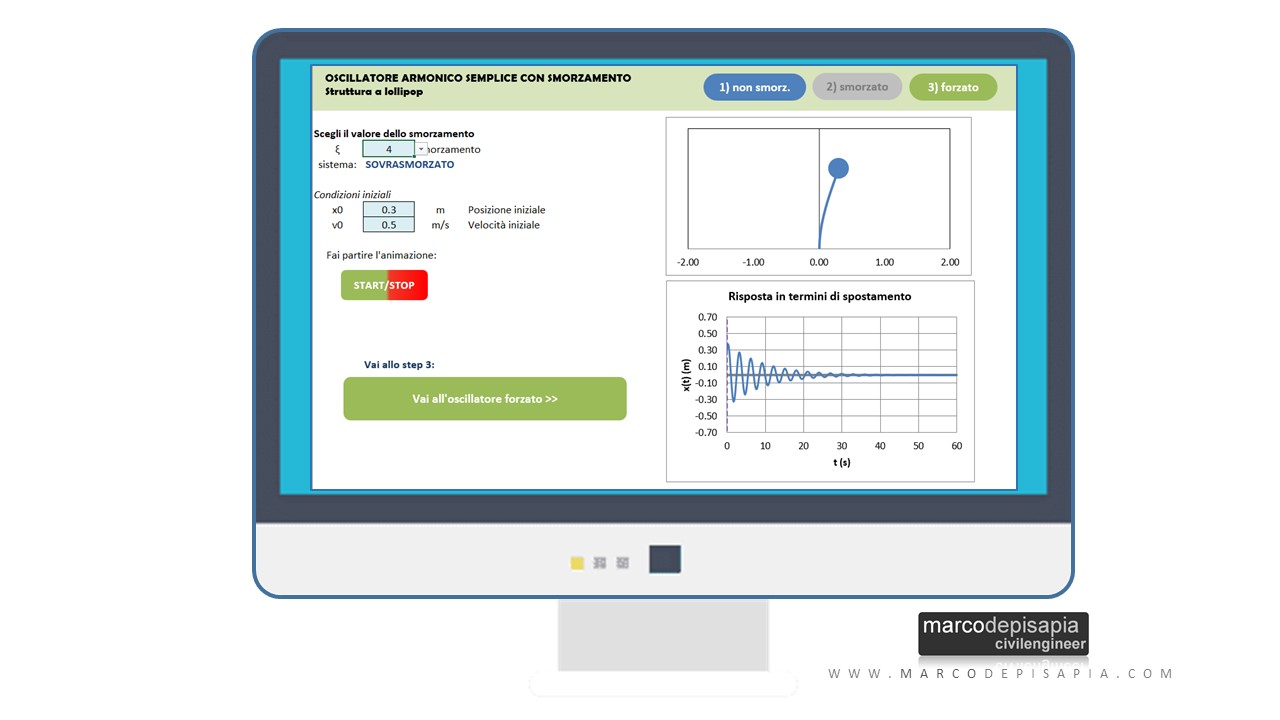
Nel modulo relativo all’oscillatore semplice smorzato della risorsa utility potrai:
- cambiare il valore dello smorzamento;
- simulare il caso di oscillatore sotto-smorzato, sovra-smorzato e con smorzamento critico;
- cambiare le condizioni iniziali: posizione iniziale e velocità;
- visualizzare il grafico della risposta in termini di spostamento in funzione del tempo;
- visualizzare l’animazione della risposta.
Potrai inoltre constatare come per un oscillatore sotto-smorzato il periodo di vibrazione sia uguale al periodo dell’oscillatore non smorzato impostando un valore dello smorzamento pari a zero.
Oscillatore semplice forzato (sistema massa-molla-smorzatore con forzante)
Se alla massa dell’oscillatore semplice, con smorzamento o senza smorzamento, applichiamo una forza orizzontale variabile nel tempo con andamento periodico di tipo sinusoidale otteniamo lo schema di oscillatore semplice forzato.
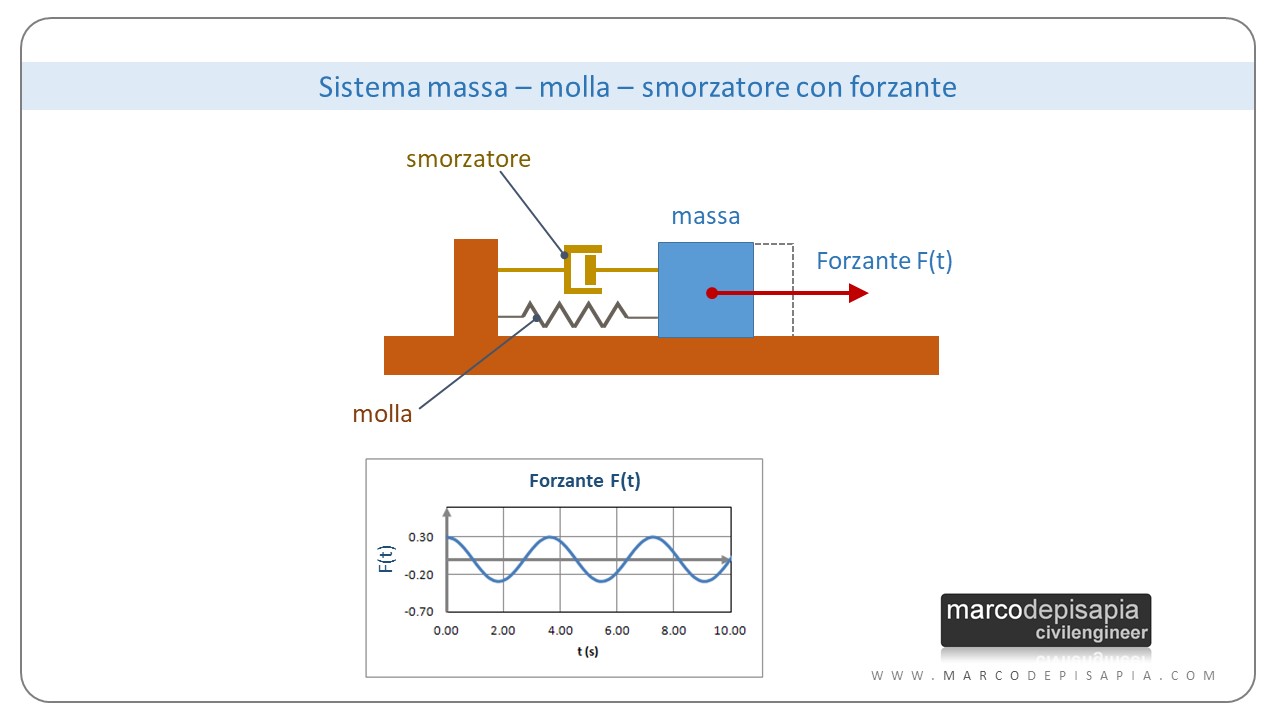
Nel caso di oscillatore smorzato, la risposta a regime dell’oscillatore sarà anch’essa di tipo sinusoidale, ma l’ampiezza delle oscillazioni dipenderà dal rapporto fra la pulsazione della forzante e la pulsazione naturale del sistema.
La pulsazione di un sistema vibrante è data dall’inverso del periodo di vibrazione secondo la seguente formula:
ω = √( k / m ) = 2π / T
- ω = pulsazione;
- T = periodo di vibrazione;
- k = rigidezza del sistema;
- m = massa del sistema.
Quando la pulsazione della forzante si avvicina alla pulsazione naturale dell’oscillatore, ovvero quando il periodo della forzante si avvicina al periodo di vibrazione dell’oscillatore, si avrà la massima ampiezza delle oscillazioni e il sistema andrà in risonanza (ricordi? Te ne ho parlato in quest’articolo).
Per un sistema in risonanza la risposta massima può essere ridotta solo aumentando lo smorzamento. Se invece lo smorzamento è nullo, la risposta del sistema in risonanza in termini di ampiezza dell’oscillazione sarà infinita.
Oscillatore forzato: amplificazione della risposta
L’ampiezza dell’oscillazione può essere descritta nel grafico dell’amplificazione in funzione del rapporto β fra la pulsazione della forzante e la pulsazione del sistema. Questo grafico indica, per ogni valore del fattore β, quante volte la risposta dinamica del sistema sarà superiore alla risposta statica ottenuta applicando al sistema una forza statica pari al valore massimo della forzante.
Nell’immagine seguente puoi vedere l’amplificazione della risposta dinamica rispetto alla risposta statica in funzione del rapporto β fra la pulsazione della forzante e la pulsazione naturale del sistema.
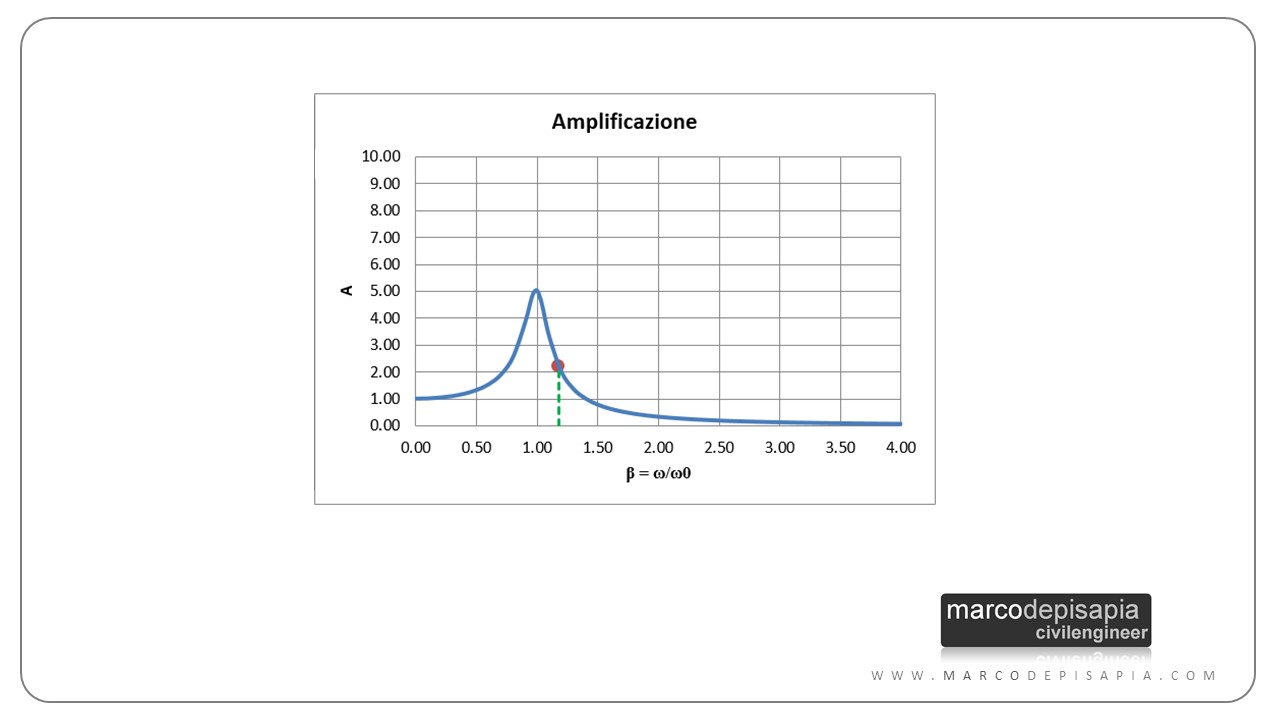
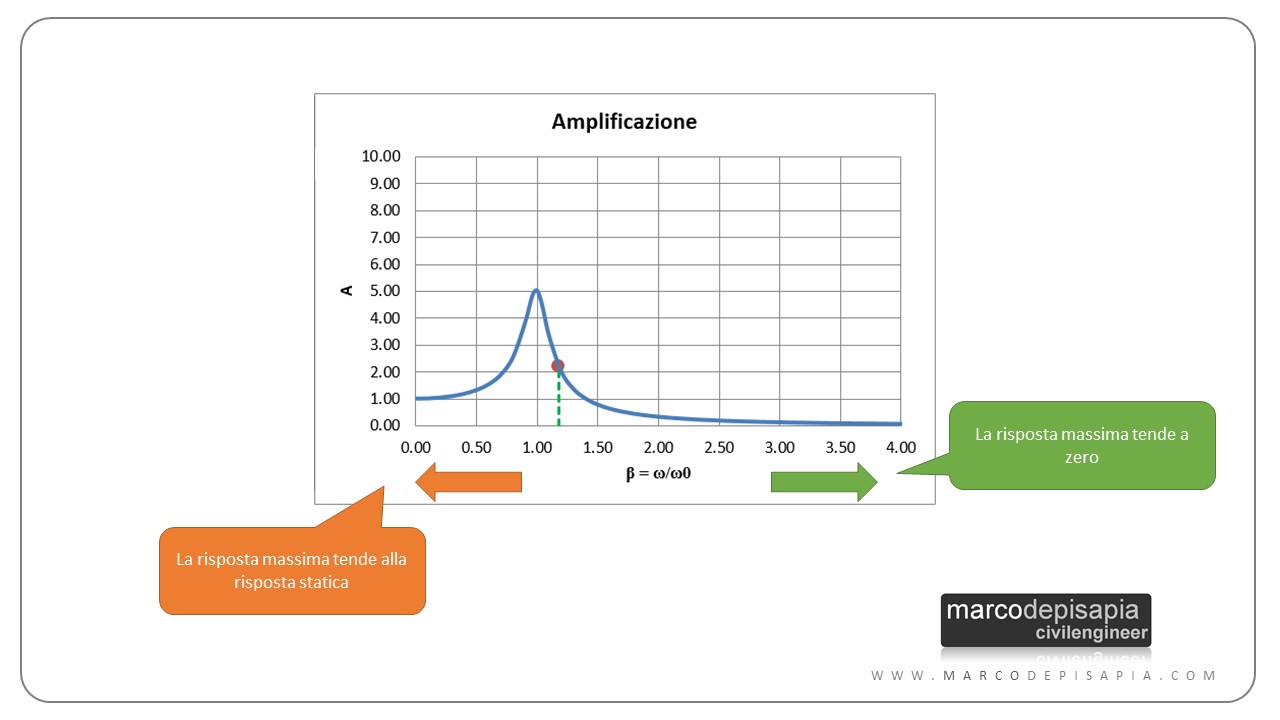
Come puoi vedere dal grafico sopra, per una pulsazione della forzante alta (β > 3 in questo caso), l’ampiezza delle oscillazioni del sistema tende a zero. Per un valore della pulsazione della forzante tendente a zero (β → 0), l’ampiezza massima dell’oscillazione del sistema si avvicinerà sempre più allo spostamento ottenuto in condizioni statiche, applicando il valore massimo della forzante. Quando la pulsazione coincide con la pulsazione naturale del sistema (β = 1), l’oscillatore andrà in risonanza.
Oscillatore forzato: simulazione interattiva con la risorsa utility
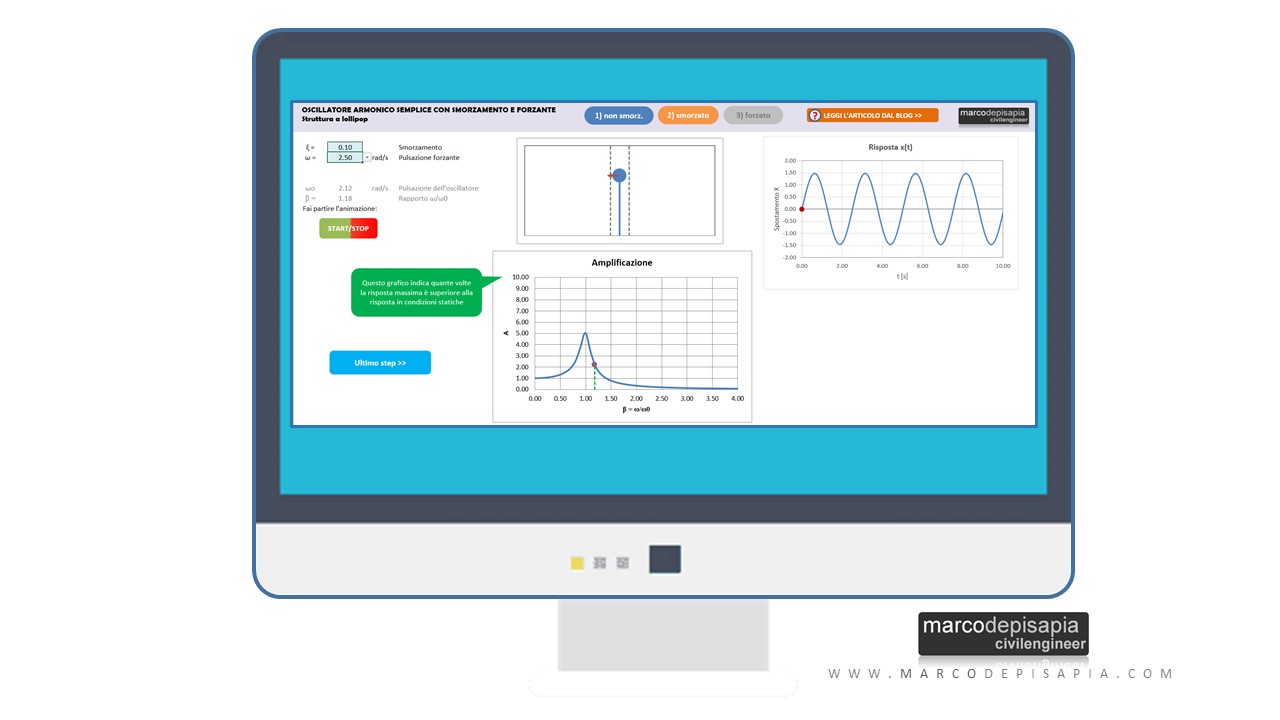
Nel modulo dedicato all’oscillatore smorzato e forzato potrai:
- cambiare il valore dello smorzamento del sistema;
- variare la pulsazione della forzante;
- visualizzare il grafico dell’amplificazione;
- visualizzare in un’animazione la risposta in termini di spostamento e il vettore della forzante.
Impostando una pulsazione della forzante molto alta, l’ampiezza delle oscillazioni del sistema tenderà a zero. Impostando un valore della pulsazione molto basso, l’ampiezza massima dell’oscillazione del sistema si avvicinerà sempre più allo spostamento ottenuto in condizioni statiche, applicando il valore massimo della forzante. Quando la pulsazione coincide con la pulsazione naturale del sistema, l’oscillatore andrà in risonanza.
Scarica la risorsa utility sull’oscillatore semplice
E’ giunto il momento di scaricare la risorsa interattiva che riproduce il comportamento dell’oscillatore semplice nei 3 casi appena visti. Compila i campi qui sotto, riceverai all’istante una mail contenente il link per eseguire il download.

Guarda la versione video dell’articolo
Ho riassunto i contenuti di questo post sul comportamento dell’oscillatore semplice in un breve video di 4 minuti. Le animazioni che vedrai nel video sono state create con Algodoo, un software molto originale che simula sistemi fisici in uno spazio bidimensionale.
Ecco cosa vedrai all’interno del video:
- oscillatore semplice – minuto 0:18;
- oscillatore smorzato – minuto 1:20;
- oscillatore con smorzamento critico – minuto 2:00
- oscillatore sovra-smorzato – minuto 2:30;
- telaio shear type – minuto 3:10;
Guarda il video, clicca sul tasto play
Conclusioni
Spero che i contenuti di quest’articolo siano stati utili per comprendere il funzionamento di un sistema fisico semplice, ma allo stesso tempo fondamentale per l’analisi sismica delle strutture. Studiando questo sistema fisico dotato di un solo grado di libertà sono stati ottenuti gli spettri di risposta che vengono utilizzati per l’esecuzione dell’analisi modale con spettro di risposta.
Se quest’articolo e la risorsa utility allegata ti sono piaciuti, puoi consigliarli ai tuoi colleghi su Linkedin o ai tuoi amici su Facebook cliccando sui pulsantini di condivisione in fondo alla pagina.
Al prossimo articolo.
Marco
Ultimo aggiornamento: 26/10/2020. Pubblicato il 6/6/2016.

Bel articolo faccio i complimenti. Mi piacerebbe che la risorsa avesse tutti i campi compilabili con valori qualsiasi e non predefiniti .
Grazie del commento. Valuterò per un futuro aggiornamento della risorsa. Ciao. Marco