Il fenomeno della risonanza può rivelarsi molto pericoloso per la sicurezza delle strutture durante un evento sismico. Edifici collocati nello stesso luogo e sottoposti allo stesso evento sismico possono subire danni nettamente differenti solo in virtù della loro differente altezza. Nell’articolo di oggi ti racconto gli effetti inaspettati di un fortissimo terremoto verificatosi a Città del Messico nel 1985. Ti risulterà subito chiaro perché l’altezza di una costruzione è così importante nella risposta di una struttura alle accelerazioni del suolo provocate da un sisma.

Alla fine del post ti mostrerò un test di laboratorio che ti aiuterà a capire in pochi secondi l’importanza critica del fenomeno della risonanza nei riguardi della sicurezza delle strutture e potrai scaricare un’utile risorsa interattiva che ti aiuterà a comprendere il comportamento dinamico delle strutture. Non perdertela.
Il terremoto di Città del Messico (gli effetti che non ti aspetti)
Anno 1985. A Città del Messico si registra un terremoto di magnitudo 8.1 sulla Scala Ricther. Fu un sisma devastante che causò il collasso di numerose strutture. L’analisi dei danni condotta dopo l’evento sismico portò alla luce una statistica degna di nota. Tutti gli edifici che riportarono seri danni strutturali o collassi avevano un’altezza compresa fra 6 e 15 piani. Gli edifici di altezza inferiore ai 6 piani e quelli con altezza maggiore di 15 piani resistettero al terremoto subendo pochissimi danni.

Ci si interrogava all’epoca sui motivi di quanto fosse accaduto. La comunità scientifica si mise subito a lavoro per analizzare il problema e ricercare le possibili spiegazioni. Sull’onda del panico post-sisma si sarebbe potuto pensare ad una soluzione rapida e sbrigativa: “non bisogna costruire edifici di altezza compresa fra 6 e 15 piani piani per evitare collassi durante i prossimi eventi sismici”.
Se la soluzione al problema fosse stata così semplice oggi non utilizzeremmo metodi di analisi avanzati come l’analisi modale e complessi software di calcolo per il progetto e verifica delle strutture in combinazione sismica. Una regola sui limiti di altezza degli edifici non avrebbe affatto messo al sicuro le nuove costruzioni, in quanto in un prossimo evento sismico avrebbe potuto verificarsi l’esatto contrario: danneggiamenti e collassi dei soli edifici alti. Ma perché? Come spiegare ciò che è accaduto a Città del Messico?
La chiave dell’enigma: il periodo di vibrazione di una struttura
Per dare una spiegazione ai collassi del terremoto di Città del Messico bisogna considerare un fattore chiave per la risposta di una struttura ad un evento sismico: il suo periodo naturale di vibrazione. In realtà è più corretto parlare di periodi di vibrazione (al plurale) in quanto ogni struttura avrà un periodo di vibrazione per ogni modo di vibrare. Il numero di modi di vibrare sarà pari al numero di gradi di libertà della struttura (tre gradi di libertà per piano nel caso di strutture con impalcati rigidi). I periodi di vibrazione dipendono da due caratteristiche fondamentali: la massa degli impalcati e la rigidezza traslante del sistema.
La massa di una struttura dipende dal peso proprio degli impalcati e dai carichi accidentali agenti. La rigidezza dipende dalle sezioni degli elementi strutturali (travi, pilastri, pareti), dalla loro disposizione in pianta e da un altro fondamentale fattore: l’altezza delle costruzioni.
Quando progettiamo una struttura, oltre a progettare le sezioni di travi, pilastri, pareti, i livelli di armatura e i dettagli costruttivi, stiamo progettando indirettamente anche la rigidezza del sistema e di conseguenza il suo periodo di vibrazione e il modo in cui l’edificio risponderà ad un evento sismico.
La risonanza mostrata in un test di laboratorio
Per spiegarti il fenomeno della risonanza ti propongo il video di un test di laboratorio eseguito su tre oscillatori semplici. I tre oscillatori hanno un solo grado di libertà, ovvero lo spostamento orizzontale e di conseguenza un solo modo di vibrare, e sono caratterizzati ciascuno da un periodo di vibrazione crescente. La massa concentrata alla sommità è uguale per tutti e tre i modelli. La differenza nel periodo di vibrazione è dovuta solo alla differente altezza dei tre modellini, crescente da sinistra a destra. La macchina utilizzata per eseguire il test applica un’oscillazione di frequenza crescente con il passare del tempo alla base dei tre modelli.
L’intero esperimento dura 3 min e 40 secondi. Se non vuoi guardare tutto il video, puoi visualizzare i minuti salienti indicati sotto per scoprire cosa succede:
- minuto 1:16;
- minuto 2:02;
- minuto 3:30.
Guarda l’esperimento sulla risonanza, clicca sul tasto Play
Risonanza: una riproduzione in scala del terremoto di Città del Messico
Hai visto cosa succede nel video? Il fenomeno di risonanza si è verificato quando la frequenza di oscillazione della base al di sotto degli oscillatori, aumentando al passare dei secondi, è arrivata a coincidere con la frequenza di oscillazione propria di ciascun modellino. I minuti che ti ho citato sopra, sono proprio i minuti in cui gli oscillatori entrano in risonanza:
- minuto 1:16 – l’oscillazione della base raggiunge una frequenza di 4 Hz (periodo = 0.25 s), la stessa del primo oscillatore sulla destra, mandandolo in risonanza;
- minuto 2:02 – frequenza di oscillazione della base pari a 6.35 Hz (periodo = 0.16 s) – risonanza del modellino centrale;
- minuto 3:30 – frequenza di oscillazione della base pari a 11.35 Hz (periodo = 0.09 s) – risonanza del modellino di sinistra.
Questo test riproduce in scala ridotta una situazione analoga a quella che si è verificata a Città del Messico. Puoi immaginare il terremoto di Città del Messico come ciò che accade al minuto 2:02, quando entra in risonanza l’oscillatore centrale di altezza intermedia fra i due. L’ampiezza di oscillazione del modellino di altezza intermedia è molto accentuata rispetto all’ampiezza di oscillazione degli altri due oscillatori che restano quasi indeformati.
Esattamente ciò che accadde a Città del Messico per gli edifici di altezza compresa fra i 6 e i 15 piani. La loro altezza faceva sì che il periodo di vibrazione di queste strutture fosse tale da mandarle in risonanza a causa delle accelerazioni sismiche a cui furono sottoposte. La frequenza delle onde sismiche generate dal terremoto di Città del Messico era molto vicina alla frequenza naturale di vibrazione delle strutture di altezza compresa fra i 6 e i 15 piani.
[Nota: frequenza e periodo di vibrazione sono due modi diversi per esprimere la stessa caratteristica di un sistema. La frequenza f è data dall’inverso del periodo di vibrazione T (f = 1/T) .]
Per completezza ti riporto la definizione rigorosa del fenomeno di risonanza:
La risonanza è una condizione fisica che si verifica quando un sistema oscillante forzato viene sottoposto a sollecitazione periodica di frequenza pari all’oscillazione propria del sistema stesso.
Come vincere la risonanza: lo spettro di risposta elastico
Al giorno d’oggi la progettazione, l’analisi e la verifica delle strutture tiene conto del fenomeno di risonanza nel calcolo dell’effetto dell’azione sismica. Ma in che modo? Attraverso gli spettri di risposta e l’esecuzione dell’analisi dinamica modale con spettro di risposta.
Lo spettro di risposta elastico relativo ad un determinato sito geografico ci dà informazioni sull’accelerazione sismica massima a cui sarà sottoposto un edificio, investito da un terremoto con una data probabilità di accadimento (periodo di ritorno pari a 475 anni per lo SLV prescritto dalla Normativa), in funzione di un solo parametro: il periodo di vibrazione della struttura.
Entrando nello spettro di risposta relativo al sito di costruzione con il periodo di vibrazione, potrai conoscere l’accelerazione sismica massima e di conseguenza l’azione sismica sollecitante.
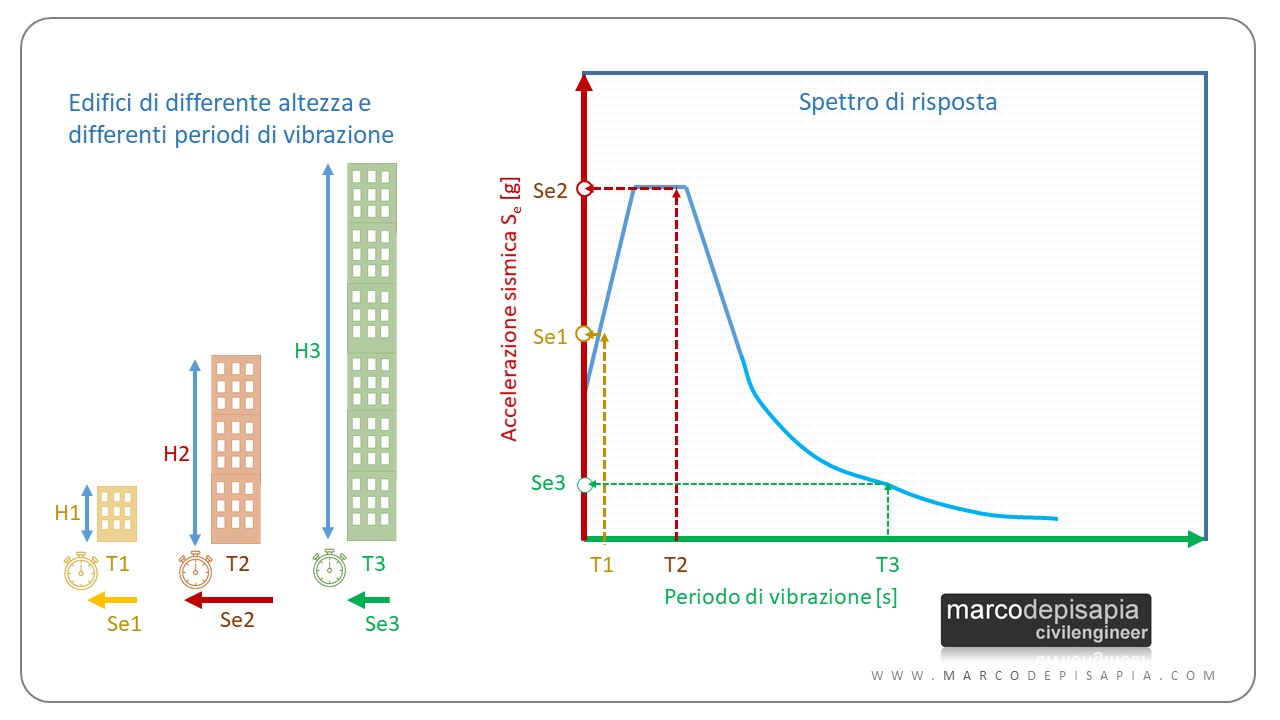
Come puoi notare, lo spettro di risposta parte da un valore dell’accelerazione pari all’accelerazione del suolo per strutture con periodo di vibrazione che tende a zero, ovvero strutture molto rigide. All’aumentare del periodo di vibrazione, l’accelerazione sismica cresce fino a raggiungere un valore massimo, che rimane costante per un tratto. All’aumentare del periodo di vibrazione, l’accelerazione sismica torna a diminuire, fino a raggiungere valori molto bassi.
Molto probabilmente gli edifici di Città del Messico con un’altezza compresa fra i 6 e i 15 piani avevano un periodo di vibrazione tale da ricadere nella zona di accelerazione massima dello spettro di risposta del sito geografico (periodo T2 nell’immagine sopra).
Il periodo di vibrazione in funzione dell’altezza delle costruzioni: la formula semplificata della Normativa Tecnica
Prima ancora di progettare le sezioni degli elementi strutturali di un edificio puoi già conoscere in maniera approssimata l’entità dell’azione sismica a cui la struttura dovrà essere in grado di resistere attraverso il calcolo approssimato del periodo di vibrazione e allo spettro di risposta. La Circolare 2019 fornisce una formula semplificata per calcolare il periodo di vibrazione in funzione dell’altezza della costruzione. Ti riporto qui sotto la formula:
T = C1 ⋅ H(3/4) – formula [C7.3.2]
- H = altezza totale della costruzione espressa in metri a partire dal piano di fondazione;
- T = periodo di vibrazione primario della struttura
Il coefficiente C1 dipende dalla tipologia strutturale:
- C1 = 0.085 per costruzioni con struttura a telaio in acciaio o legno;
- C1 = 0.075 per costruzioni con struttura a telaio in calcestruzzo armato;
- C1 = 0.050 per costruzioni con struttura di muratura o di qualsiasi altro tipo.
Circolare 2019 – par. C7.3.3.2
Scarica la risorsa utility sull’oscillatore semplice
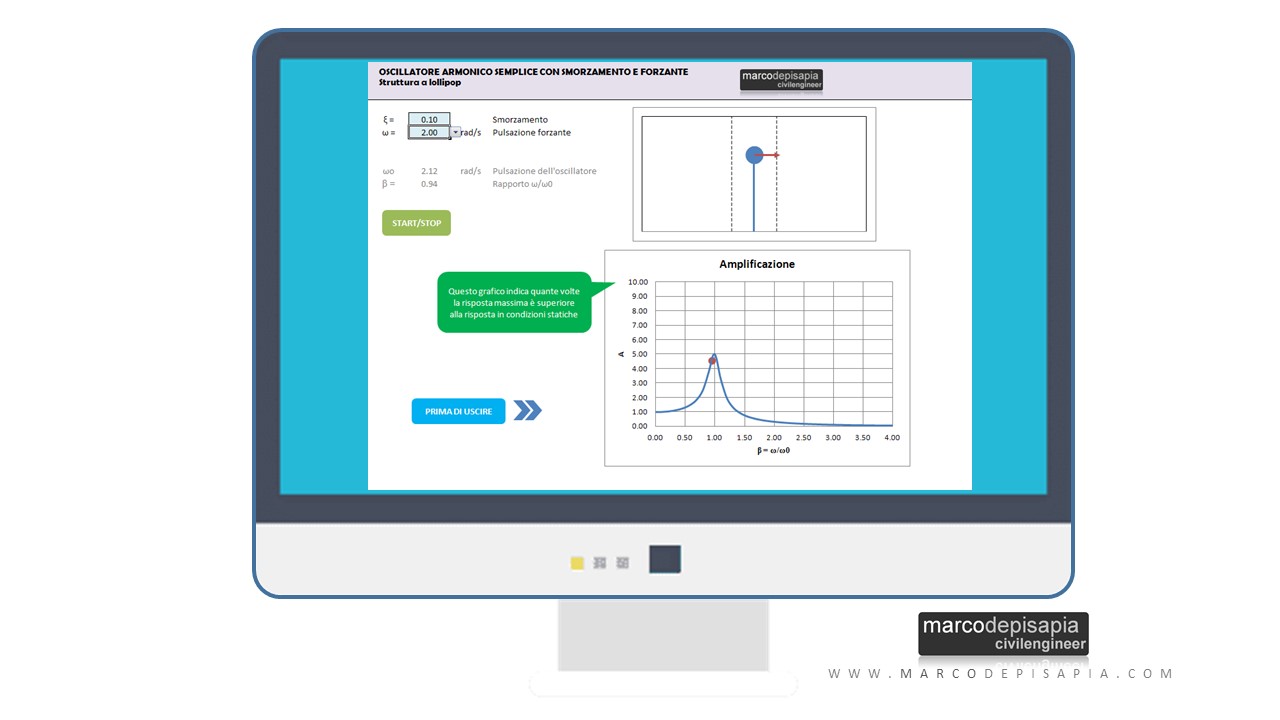 Per visualizzare gli effetti della risonanza su un oscillatore semplice sollecitato da una forzante, scarica la risorsa utility interattiva. Potrai variare il periodo di vibrazione dell’oscillatore e visualizzare la risposta del sistema in presenza di una forzante. Per scaricare la risorsa compila i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download.
Per visualizzare gli effetti della risonanza su un oscillatore semplice sollecitato da una forzante, scarica la risorsa utility interattiva. Potrai variare il periodo di vibrazione dell’oscillatore e visualizzare la risposta del sistema in presenza di una forzante. Per scaricare la risorsa compila i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download.

Conclusioni
L’analisi sismica delle strutture ha visto compiere grossi passi avanti nel corso degli anni. Si è passati da uno scenario in cui, prima dell’avvento dei computer, le strutture venivano analizzate e calcolate per soli carichi statici verticali. Oggi, per garantire la sicurezza, le strutture si analizzano mediante modelli spaziali tridimensionali e l’effetto del sisma su una struttura si valuta grazie ad uno spettro di risposta e ad un tipo avanzato di analisi: l’Analisi Dinamica Modale.
Tutto ciò è stato possibile grazie all’osservazione degli effetti di eventi sismici sulle costruzioni e allo studio delle strutture in campo dinamico. L’enorme potenza di calcolo di cui disponiamo oggi ha reso possibile per tutti i progettisti strutturali eseguire analisi che, prima della massiccia diffusione dei computer, erano un’esclusiva dei centri di ricerca. Di conseguenza però tutto è diventato più complesso e mantenere il controllo sui risultati di queste analisi non è così scontato. Per questo motivo ho raccolto e rielaborato diversi articoli del blog sull’argomento per creare EarthQuake: la guida pratica per l’analisi sismica delle strutture. Puoi leggere l’estratto gratuito in formato pdf a questo link.
Hai trovato interessante quest’articolo? Se il post ti è piaciuto e vuoi condividerlo con i tuoi colleghi su Linkedin o con i tuoi amici su Facebook, puoi cliccare sui pulsantini di condivisione social in fondo alla pagina. Che ne pensi dell’esperimento visto nel video? Mi piacerebbe conoscere un tuo parere nei commenti.
Al prossimo articolo.
Marco
Aggiornato il 3/11/2019. Pubblicato il 1/2/2016.


Ciao. Ho appena preso il tuo libro che sto leggendo con molto interesse. Ho però notato che questo articolo è stato aggiornato anche per l’entrata in vigore delle NTC 2018 e la pubblicazione della circolare, il libro però non tiene conto di questa evoluzione. Ci sarà una versione aggiornata della pubblicazione?
Ciao Manfredi, si ci sarà una versione aggiornata della guida EarthQuake. Sarai avvisato tramite newsletter non appena sarà disponibile.
bravo
Grazie del commento 😉
Articolo interessantissimo, utile anche per gli Architetti.
Grazie del commento, mi fa piacere ti sia stato utile 🙂