Quando eseguiamo l’analisi strutturale di una costruzione in zona sismica, il nostro software di calcolo genera ben 32 combinazioni sismiche di carico. Come vengono generate tutte queste combinazioni? In quest’articolo ti mostro i 3 fattori chiave che entrano in gioco nella creazione delle combinazioni di carico in presenza dell’azione sismica e come vengono generate le 32 combinazioni da considerare nell’analisi.

Alla fine dell’articolo potrai scaricare un Focus Normativo PDF che raccoglie tutte le prescrizioni delle NTC2018 e Circolare 2019 sulle combinazioni sismiche. Nel corso dell’articolo scoprirai come implementare ulteriori combinazioni di carico per aumentare il livello di sicurezza della strutture in zona sismica, arrivando a ben 64 combinazioni totali. Continua a leggere per saperne di più.
32 combinazioni sismiche: i 3 fattori chiave che le generano
Le relazioni di calcolo strutturale prodotte dai software di calcolo contengono centinaia di pagine e tabulati. Uno dei motivi che rende i fascicoli di calcolo così voluminosi è senza dubbio l’elevato numero di combinazioni di carico in condizioni sismiche.
Intuitivamente possiamo immaginare combinazioni di carico molto meno numerose se pensiamo all’azione sismica agente lungo due direzioni ortogonali (X e Y) . In prima battuta verrebbero in mente solo 4 combinazioni:
- azione sismica lungo X con verso positivo
- azione sismica lungo X con verso negativo
- azione sismica lungo Y con verso positivo
- azione sismica lungo Y con verso negativo
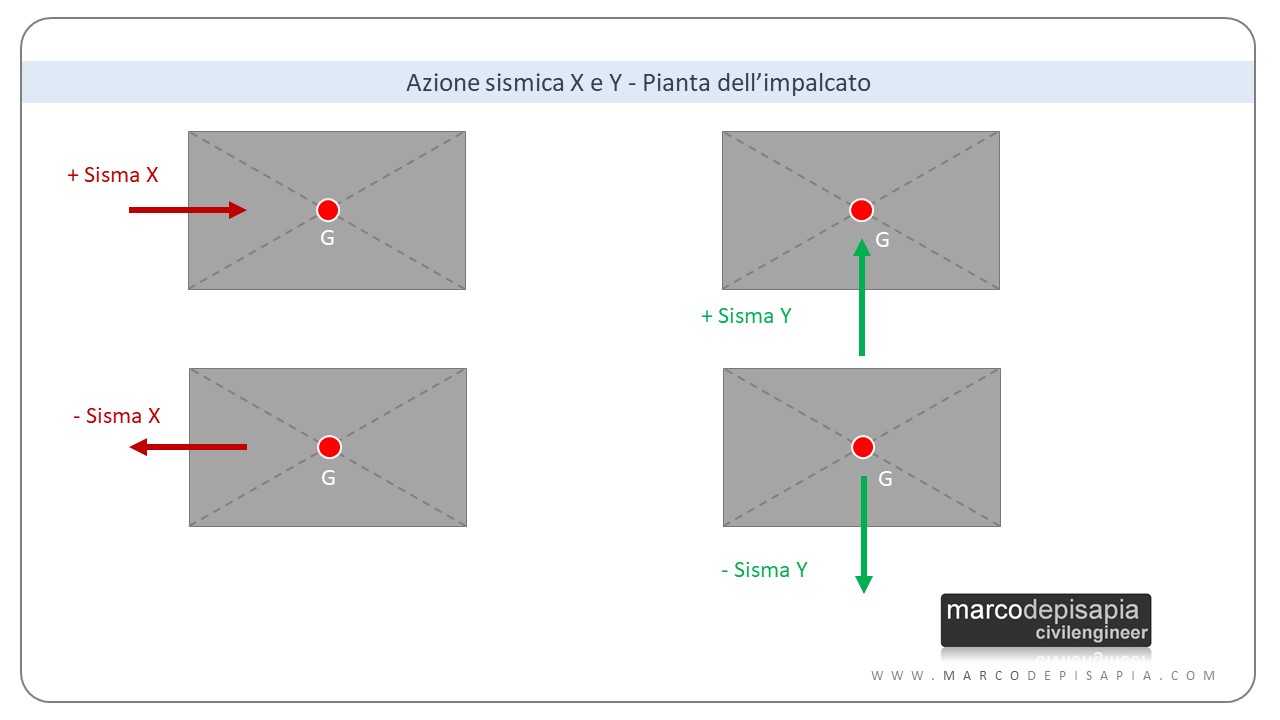
Come possiamo spiegarci le altre 28 combinazioni di carico che vanno a comporre in totale le 32 combinazioni sismiche? Per capire come vengono generate tutte le combinazioni di carico sismiche dobbiamo considerare tre fattori fondamentali. Ti assicuro che alla fine di quest’articolo ti sarà tutto più chiaro e le 32 combinazioni di carico non ti sembreranno più un’esagerazione. Ti elenco di seguito i tre fattori chiave che danno vita alle 32 combinazioni di carico per azioni sismiche.
1. Combinazioni sismiche: l’eccentricità del centro di massa
L’azione sismica è applicata nel baricentro delle masse di ciascun impalcato di piano. Se l’impalcato ha una pianta rettangolare, il baricentro delle masse coinciderà con il baricentro geometrico del rettangolo. Ma è una situazione verosimile? Proviamo a pensarci. La massa di un impalcato è composta da:
- peso proprio degli elementi strutturali del solaio (per esempio travetti, soletta, pignatte per solai latero-cementizi)
- peso proprio degli elementi permanenti non strutturali (pavimento, massetto, intonaco, tramezzi etc)
- peso dei carichi accidentali (suppellettili, presenza di persone etc.)
Assumere il baricentro delle masse coincidente con il baricentro geometrico della pianta dell’impalcato equivale a dire che tutti i carichi accidentali sono posizionati in modo tale da far coincidere il centro di massa con il baricentro geometrico dell’impalcato.
E’ molto difficile che si verifichi una situazione del genere nella realtà. Per questo motivo la Normativa Tecnica prescrive un accorgimento da adottare per tenere conto della casualità nella posizione reale dei carichi.
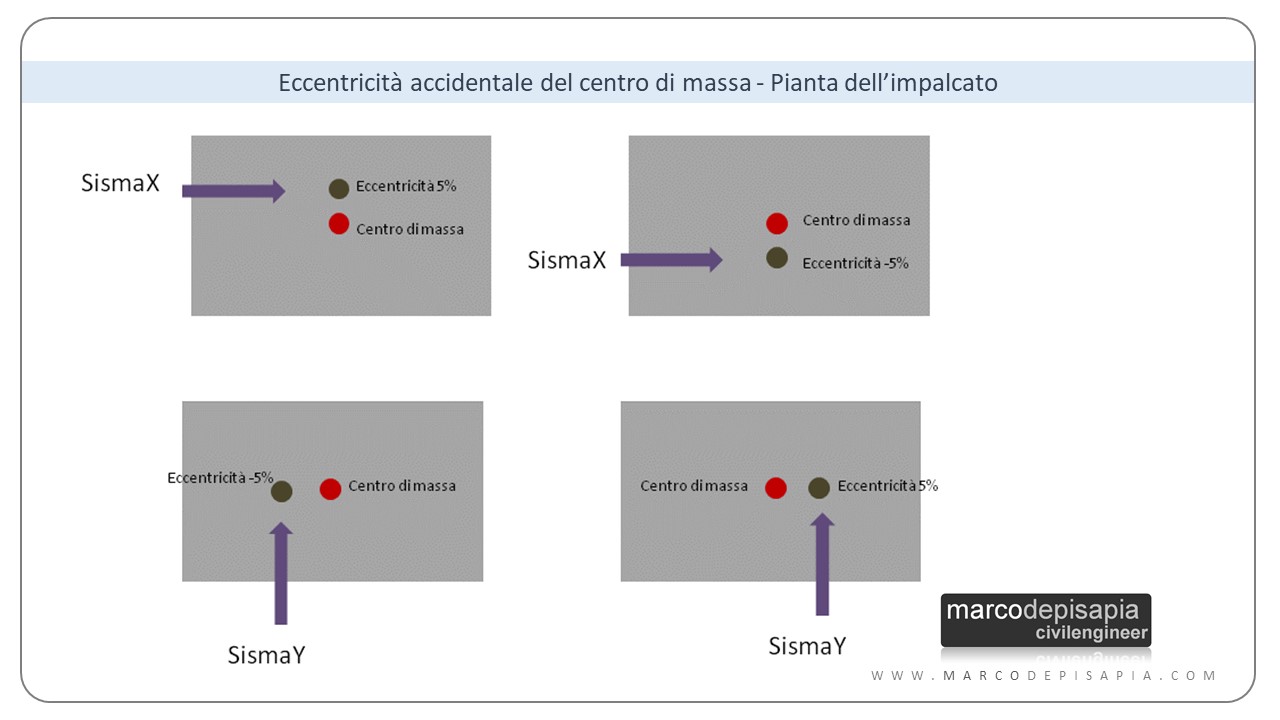
Per tenere conto della variabilità spaziale del moto sismico, nonché di eventuali incertezze [nella localizzazione delle masse, n.d.a.], deve essere attribuita al centro di massa un’eccentricità accidentale rispetto alla sua posizione quale deriva dal calcolo. Per i soli edifici e in assenza di più accurate determinazioni, l’eccentricità accidentale in ogni direzione non può essere considerata inferiore a 0,05 volte la dimensione media dell’edificio misurata perpendicolarmente alla direzione di applicazione dell’azione sismica. Detta eccentricità è assunta costante, per entità e direzione, su tutti gli orizzontamenti.
NTC2018 par. 7.2.6
L’eccentricità del centro di massa darà vita di conseguenza a quattro differenti posizioni del baricentro delle masse. Avremo dunque quattro differenti “pacchetti” di combinazioni sismiche, uno per ogni posizione del centro di massa. Nella figura qui sotto puoi vedere schematizzate le quattro differenti posizioni delle masse.
2. Sisma prevalente in una direzione e sisma in direzione ortogonale
Il secondo fattore che genera 32 combinazioni sismiche è la presenza contemporanea dell’azione sismica in direzione X e Y, come prescritto dalle NTC2018 al par. 7.3.5. (troverai l’estratto nel Focus Normativo PDF scaricabile alla fine del post).
Insieme con l’azione sismica prevalente in una direzione, agirà in contemporanea il 30% dell’azione sismica nella direzione ortogonale.
Esempio: per sisma prevalente in direzione X, agirà il 30% dell’azione sismica in direzione Y. Per sisma prevalente in direzione Y, agirà il 30% dell’azione sismica in direzione X.
La contemporaneità dell’azione sismica lungo due direzioni ortogonali (X e Y) va considerata per le quattro differenti posizioni del centro di massa generate dall’eccentricità accidentale, citata prima. Ti riporto di seguito le combinazioni che si ottengono considerando la contemporaneità del sisma nelle due direzioni X e Y.
- Posizione 1 del centro di massa
- SismaX + 0.3 * SismaY
- 0.3 * SismaX + SismaY
- Posizione 2 del centro di massa
- SismaX + 0.3 * SismaY
- 0.3 * SismaX + SismaY
- Posizione 3 del centro di massa
- SismaX + 0.3 * SismaY
- 0.3 * SismaX + SismaY
- Posizione 4 del centro di massa
- SismaX + 0.3 * SismaY
- 0.3 * SismaX + SismaY
Siamo arrivati finora ad 8 combinazioni, ovvero 2 combinazioni per ciascuna posizione del centro di massa. I conti ancora non tornano. Mancano 24 combinazioni per arrivare alle 32 combinazioni sismiche. Non ci resta che considerare l’ultimo fattore che influisce sulla creazione delle combinazioni di carico in presenza di sisma.
3. Combinazioni sismiche: verso positivo e negativo dell’azione sismica
L’ultimo elemento da considerare per generare le 32 combinazioni sismiche è il verso positivo o negativo dell’azione sismica, lungo le due direzioni ortogonali (X e Y) in cui il sisma può agire.
La permutazione dei segni positivo e negativo, insieme con l’eccentricità delle masse e la contemporaneità del sisma lungo due direzioni ortogonali darà vita alle 32 combinazioni di carico da considerare per l’analisi delle costruzioni in zona sismica.
32 combinazioni sismiche: l’elenco completo
Ti elenco di seguito le 32 combinazioni sismiche raggruppate per le 4 differenti posizioni del centro di massa.
- Posizione 1 del centro di massa (+5%, +5%)
- Sisma prevalente X:
- 1) + SismaX + 0.3 * SismaY
- 2) + SismaX – 0.3 * SismaY
- 3) – SismaX + 0.3 * SismaY
- 4) – SismaX – 0.3 * SismaY
- Sisma prevalente Y:
- 5) + 0.3 * SismaX + SismaY
- 6) + 0.3 * SismaX – SismaY
- 7) – 0.3 * SismaX + SismaY
- 8) – 0.3 * SismaX – SismaY
- Sisma prevalente X:
Le 8 combinazioni viste sopra vanno ripetute per le restanti tre posizioni del centro di massa.
- Posizione 2 del centro di massa (+5%, -5%)
- [Si ripetono le stesse 8 combinazioni viste per la posizione 1 del centro di massa]
- Posizione 3 del centro di massa (-5%, +5%)
- [Si ripetono le stesse 8 combinazioni viste per la posizione 1 del centro di massa]
- Posizione 4 del centro di massa (-5%, -5%)
- [Si ripetono le stesse 8 combinazioni viste per la posizione 1 del centro di massa]
Siamo finalmente giunti al numero complessivo di 32 combinazioni sismiche: 8 combinazioni x 4 posizioni del centro di massa = 32 combinazioni sismiche totali.
Da 32 a 64 combinazioni sismiche: come aumentare la sicurezza delle strutture
Vedremo nel seguito del post un utile accorgimento per aumentare il livello di sicurezza di una costruzione in zona sismica, considerando delle combinazioni di carico sismiche aggiuntive oltre alle 32 combinazioni sismiche appena viste.
Le combinazioni sismiche aggiuntive consistono in una duplicazione delle 32 combinazioni con l’aggiunta di una variante. Nelle nuove 32 combinazioni sismiche verrà utilizzato un coefficiente di combinazione pari a zero per i carichi accidentali, ipotizzando che tali carichi diano un contributo favorevole alle verifiche di resistenza.
Annullando i carichi accidentali agenti, diminuirà lo sforzo normale nei pilastri e di conseguenza cambierà il momento resistente. Nel dominio di resistenza momento-sforzo normale di una sezione in cemento armato (ma anche per i pilastri in acciaio vale stesso principio) il momento resistente dipende dall’entità dello sforzo normale agente. Facendo variare lo sforzo normale nei pilastri, il momento resistente può aumentare oppure diminuire a seconda della zona del dominio M-N in cui va a collocarsi lo stato di sollecitazione.
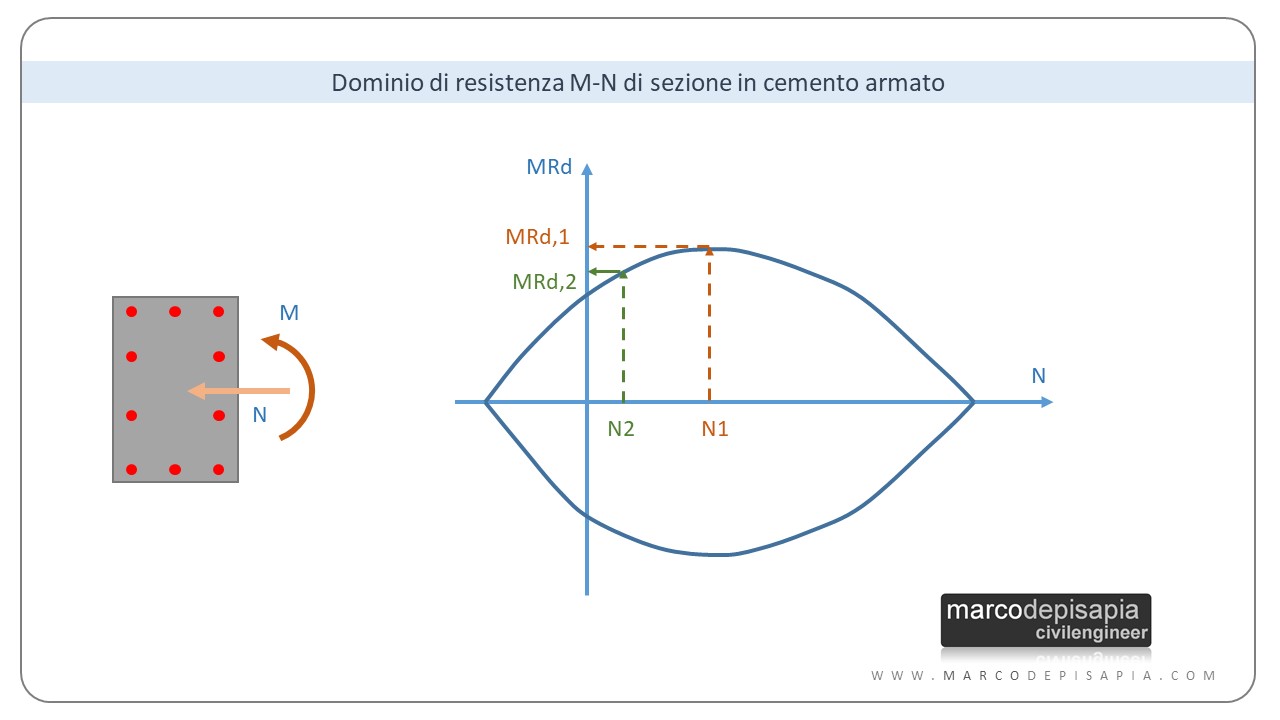
Considerare le 32 combinazioni di carico aggiuntive appena viste, ci darà la certezza che gli elementi strutturali siano verificati in assenza di carichi accidentali e in presenza dell’azione sismica.
Scarica il Focus Normativo PDF sulle combinazioni sismiche
![]()
Ho raccolto tutte le prescrizioni della Normativa Tecnica NTC2018 e della Circolare 2019 riguardanti i fattori che entrano in gioco per la creazione delle 32 combinazioni di carico sismiche in unico documento PDF scaricabile gratuitamente. Compila i campi qui sotto, riceverai all’istante un’email contenente il link per eseguire il download.

Guarda il video dell’articolo – clicca su Play
Eccentricità del centro di massa: come valutarne l’effetto nell’analisi sismica
L’eccentricità accidentale del centro di massa, oltre a contribuire alla creazione delle 32 combinazioni di carico, può determinare un’ulteriore discriminante nell’analisi sismica delle strutture. Per tener conto dell’effetto dell’eccentricità accidentale del centro di massa è infatti possibile seguire due strade alternative:
- una soluzione approssimata che consiste nell’applicare carichi statici (momenti torcenti) ad ogni impalcato;
- una soluzione rigorosa, ma più onerosa dal punto di vista computazionale, che consiste nell’eseguire 4 volte l’analisi modale della struttura, ovvero una volta per ognuna delle 4 posizioni del centro di massa;
Vediamo nel dettagli queste due differenti soluzioni.
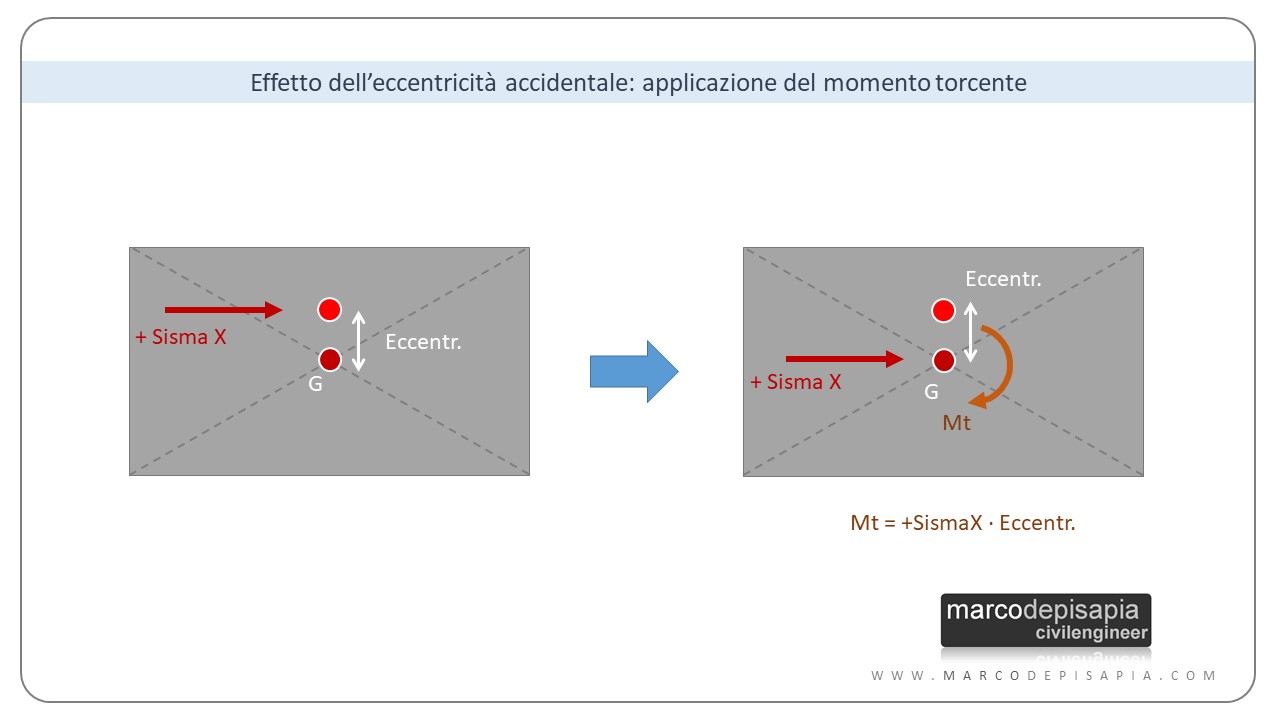
Effetto dell’eccentricità accidentale: applicazione di momenti torcenti
La normativa tecnica NTC2018 prescrive che gli effetti dell’eccentricità accidentale del centro di massa possono essere tenuti in conto applicando un momento torcente (quindi un carico statico) ad ogni impalcato. Il momento torcente sarà pari al prodotto fra la forza sismica orizzontale di piano, determinata mediante analisi lineare statica, e l’eccentricità accidentale del baricentro delle masse.
Effetto dell’eccentricità accidentale: valutazione mediante analisi modale
L’eccentricità accidentale del centro di massa darà vita a 4 diverse posizioni del baricentro delle masse per ogni impalcato. L’effetto di tale eccentricità, in termini di sollecitazioni e spostamenti, può essere valutato mediante l’esecuzione dell’analisi modale.
In tal caso l’analisi modale verrà eseguita quattro volte, una per ogni posizione del centro di massa. I modi vibrare di un sistema dipendono infatti, oltre che dalla rigidezza del sistema, anche dalla distribuzione delle masse. Per ciascuna posizione del centro di massa avremo modi di vibrare e periodi di vibrazione leggermente diversi fra loro.
Scarica la risorsa utility sui modi di vibrare di un telaio piano
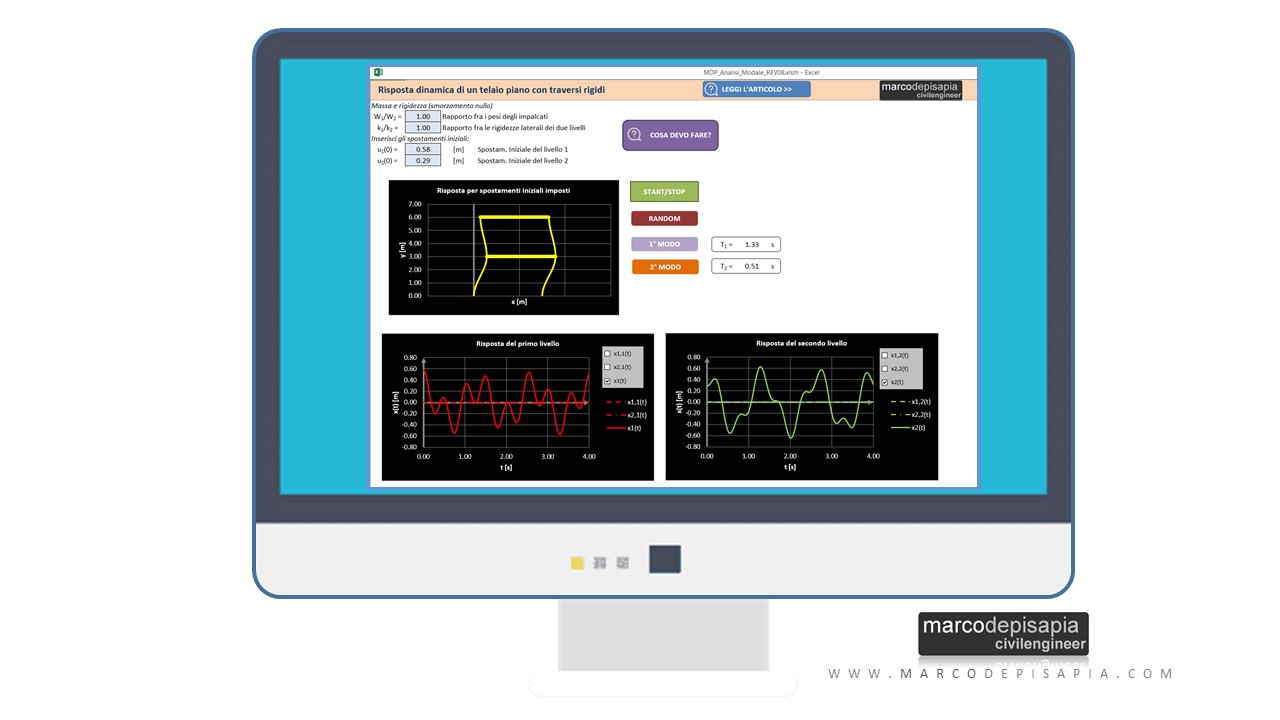
Per renderti conto dell’influenza della distribuzione delle masse sui modi di vibrare di una struttura puoi scaricare una risorsa utility che riproduce, mediante animazioni interattive, i modi di vibrare di un telaio piano a due livelli. Facendo variare la massa dei due impalcati, cambieranno i modi di vibrare e i periodi propri di vibrazione.
All’interno della risorsa potrai variare il rapporto fra la massa del primo e del secondo impalcato e visualizzare la variazione dei modi di vibrare del sistema. Compila i campi qui sotto per scaricare la risorsa. Riceverai all’istante una mail contenente il link per eseguire il download.

Conclusioni
L’articolo di oggi finisce qui. Spero che ora ti risulti più chiaro come vengono generate le 32 combinazioni di carico in presenza dell’azione sismica. E tu quante combinazioni di carico implementeresti per eseguire l’analisi di una costruzione in zona sismica, 32 o 64? Puoi farmelo sapere in un commento all’articolo. Se l’articolo ti è piaciuto, puoi condividerlo con i tuoi colleghi su Linkedin e con i tuoi amici su Facebook, cliccando sui tasti di condivisione social in fondo alla pagina.
Al prossimo post.
Marco
Ultimo aggiornamento: 20/12/2020. Pubblicato il 29/2/2016.

Pingback:Azione sismica: come ottenere 32 combinazioni di carico [video]